"

2.4 Solving Using the Square Root Method

2.4.1 Preview

Example

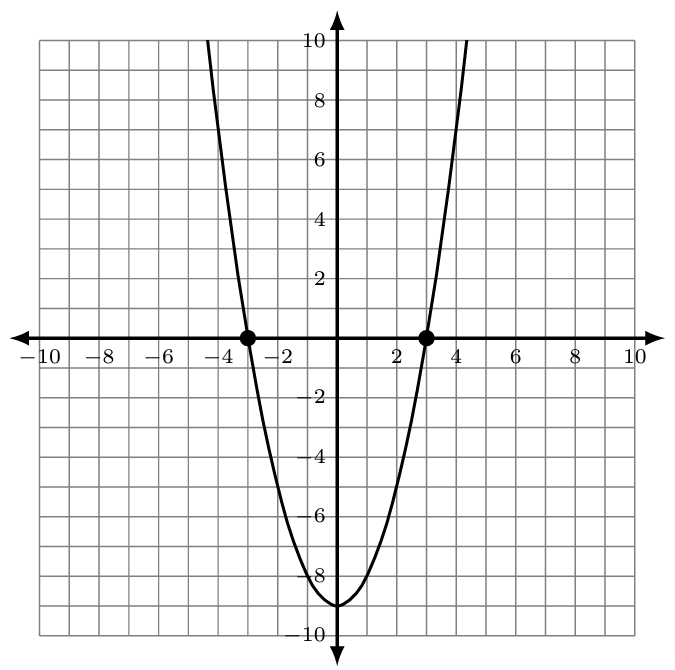
The graph of [latex]f\left(x\right)=x^2-9[/latex] is given. Notice the graph has symmetry over the y-axis and that the x-intercepts, (-3,0) and (3,0), are also symmetric.

[latex]\begin{array}{rcl}f(x)&=&x^2-9\\x^2-9&=&0\\x^2-\cancel9+\cancel9&=&0+9\\x^2&=&9\\\sqrt{x^2}&=&\sqrt9\\\vert x\vert&=&3\\x&=&\pm3\end{array}[/latex]

A parabola is graphed on a Cartesian coordinate system. The x-axis ranges from -10 to 10, and the y-axis ranges from -10 to 10, with integer markings. The parabola opens upwards, with its vertex at (0, -9). It intersects the y-axis at (0, -9) and the x-axis at (-3, 0) and (3, 0).

Example

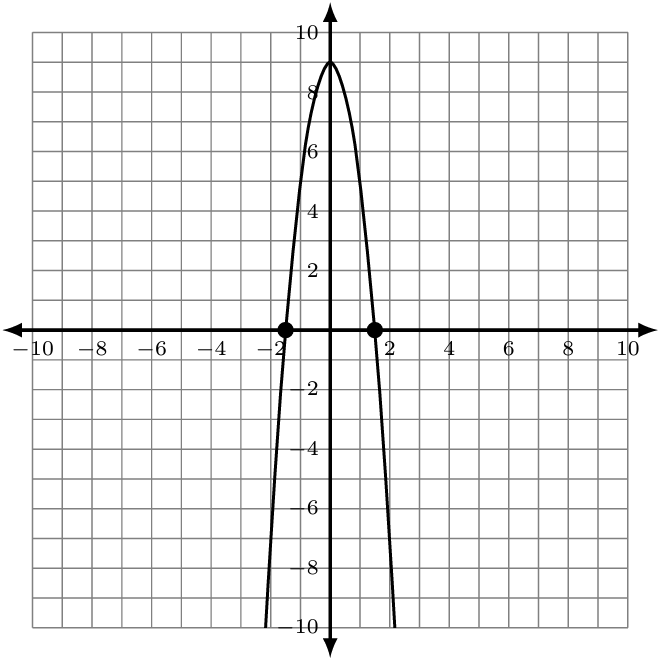
The graph of [latex]f\left(x\right)=9-4x^2[/latex] is given. Notice the graph has symmetry over the y-axis and that the x-intercepts are also symmetric.

[latex]\begin{array}{rcl}f(x)&=&9-4x^2\\9-4x^2&=&0\\9-\cancel{\mathcal4\mathcal x^{\mathcal2}}+\cancel{\mathcal4\mathcal x^{\mathcal2}}&=&0+4x^2\\9&=&4x^2\\\frac94&=&x^2\\\sqrt{\frac94}&=&\sqrt{x^2}\\\frac32&=&\vert x\vert\\\pm\frac32&=&x\end{array}[/latex]

A parabola is graphed on a Cartesian coordinate system. The x-axis ranges from -10 to 10, and the y-axis ranges from -10 to 10, with integer markings. The parabola opens downwards, with its vertex at approximately (0, 9). It intersects the y-axis at (0, 9) and the x-axis at (-1.5, 0) and (1.5, 0).

Example

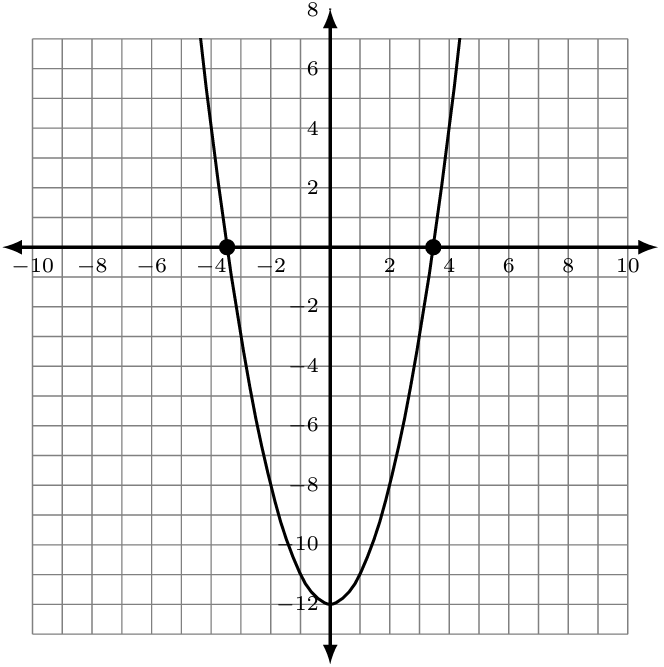
The graph of [latex]f\left(x\right)=x^2-12[/latex] given. Notice the graph has symmetry over the y-axis and that the x-intercepts are also symmetric.

[latex]\begin{array}{rclc}f(x)&=&x^2-12&{}\\x^2-12&=&0&{}\\x^2-\cancel{12}+\cancel{12}&=&0+12&{}\\x^2&=&12&{}\\\sqrt{x^2}&=&\sqrt{12}&{}\\\vert x\vert&=&2\sqrt3&{}\\x&=&\pm2\sqrt3&(\mathrm{exact})\\x&\approx&\pm3.464&(\mathrm{approximate})\end{array}[/latex]

A parabola is graphed on a Cartesian coordinate system. The x-axis ranges from -10 to 10, and the y-axis ranges from -12 to 8, with integer markings. The parabola opens upwards, with its vertex at approximately (0, -12). It intersects the y-axis at (0, -12) and the x-axis at approximately (-3.4, 0) and (3.4, 0).

Example

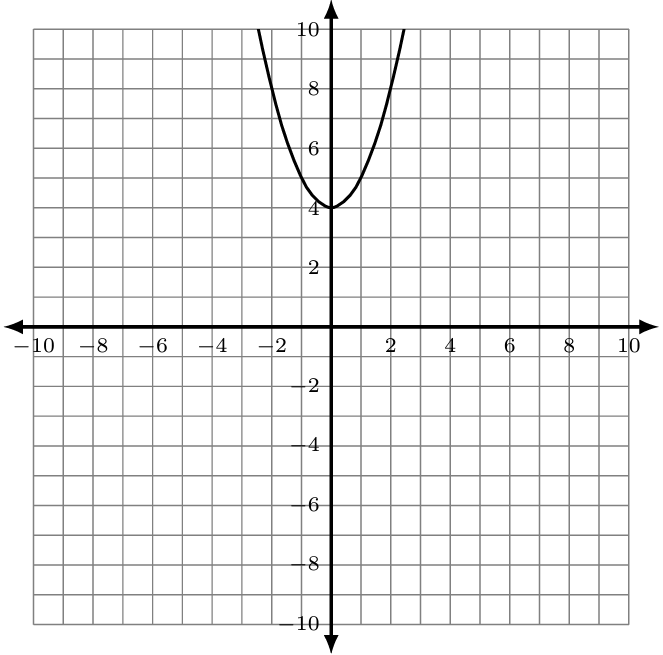
The graph of [latex]f\left(x\right)=x^2+4[/latex] given. Notice the graph has symmetry over the y-axis, but it has no x-intercepts.

[latex]\begin{array}{rcl}f(x)&=&x^2+4\\x^2+4&=&0\\x^2+\cancel4-\cancel4&=&0-4\\x^2&=&-4\\\sqrt{x^2}&=&\sqrt{-4}\\\vert x\vert&=&2i\\x&=&\pm2i\end{array}[/latex]

A parabola is graphed on a Cartesian coordinate system. The x-axis ranges from -10 to 10, and the y-axis ranges from -10 to 10, with integer markings. The parabola opens upwards, with its vertex at approximately (0, 4). It intersects the y-axis at (0, 4) and does not appear to intersect the x-axis.

2.4.2 Classwork

Solve using the Square Root Method.

  1. [latex]x^2-16=0[/latex]
  2. [latex]x^2-100=0[/latex]
  3. [latex]x^2+25=0[/latex]
  4. [latex]x^2+88=7[/latex]
  5. [latex]x^2+7=4[/latex]
  6. [latex]x^2-4=-5[/latex]
  7. [latex]6x^2=90[/latex]
  8. [latex]99-4x^2=0[/latex]
  9. [latex]\frac34x^2=12[/latex]
  10. [latex]49x^2+16=8[/latex]
  11. [latex]x^2+5=17[/latex]
  12. [latex]x^2-41=0[/latex]
  13. [latex]-8x^2-6=-30[/latex]
  14. [latex]x^2-17=6[/latex]
  15. [latex]\frac12x^2-29=3[/latex]
  16. [latex]\frac34x^2+\frac13=0[/latex]

Answer the following.

  1. In science class, students were asked to create a container to hold an egg which they would then drop from a window. The function [latex]h\left(t\right)=-16t^2+25[/latex] gives the container’s height h (in feet) after t seconds. How many seconds will it take for the container to hit the ground?
  2. Use the equation [latex]9x^2-5=0[/latex] to answer the following.
    1. Solve using the Quadratic Formula.
    2. Solve using the Square Root Method.
    3. Discuss the differences between (a) and (b). State which method you prefer and why.
  3. Under what conditions for [latex]ax^2+bx+c=0[/latex] can you solve using the Square Root Method? Explain.
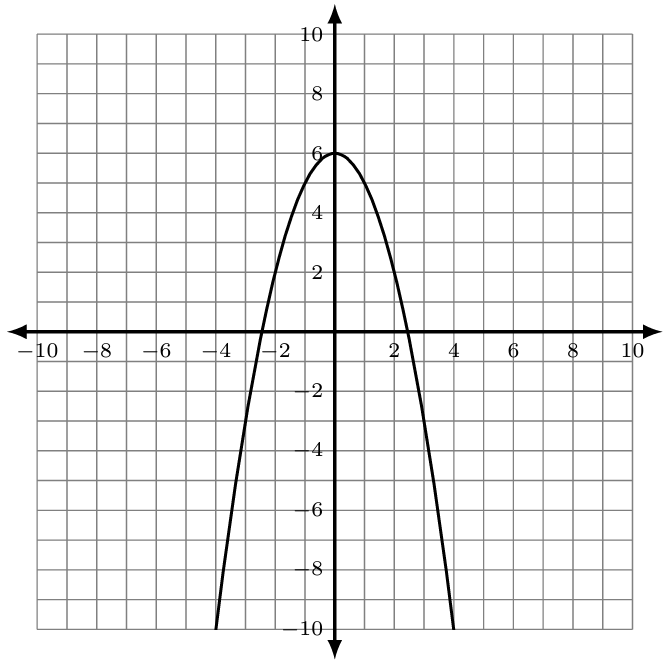
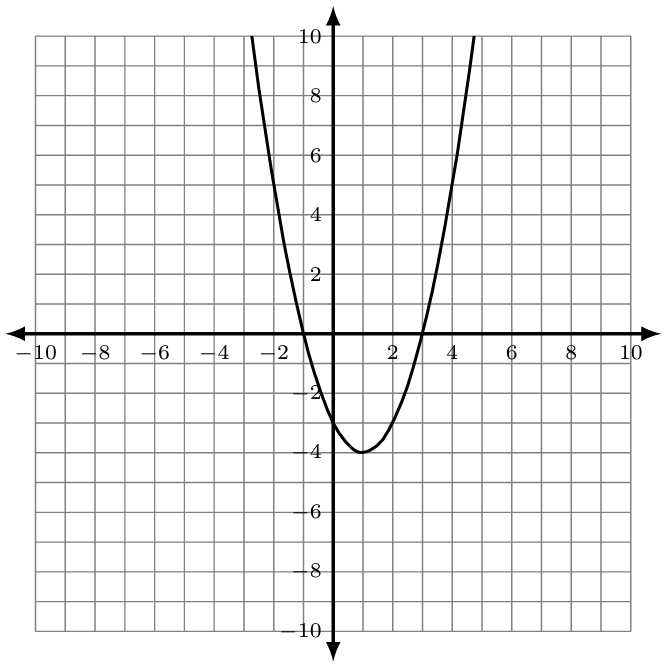
  4. For which of the following graphs could you use the Square Root Method to solve for the x-intercepts? Explain.

A parabola is graphed on a Cartesian coordinate system. The x-axis ranges from -10 to 10, and the y-axis ranges from -10 to 10, with integer markings. The parabola opens downwards, with its vertex at (0, 6). It intersects the y-axis at (0, 6) and the x-axis at approximately (-2.5, 0) and (2.5, 0).A parabola is graphed on a Cartesian coordinate system. The x-axis ranges from -10 to 10, and the y-axis ranges from -10 to 10, with integer markings. The parabola opens upwards, with its vertex at approximately (1, -4). It intersects the y-axis at (0, -3) and the x-axis at (-1, 0) and (3, 0).

2.4.3 Homework

  1. Compare and contrast [latex]f\left(x\right)=x^2-4\;\text{and}\;\;\;g\left(x\right)=x^2+4.[/latex]

Solve using the Square Root Method.

  1. [latex]x^2-49=0[/latex]
  2. [latex]2x^2-6=0[/latex]
  3. [latex]5x^2+20=0[/latex]
  4. [latex]4x^2+81=0[/latex]
  5. [latex]\frac1{10}x^2-\frac{23}5=0[/latex]
  6. [latex]\frac13x^2+\frac14=\frac{115}{12}[/latex]

Graph and identify the following characteristics for the function.

  1. [latex]g\left(x\right)=4x^2-5[/latex]

    Opens: Up / Down

    Axis of Symmetry:

    Vertex:

    y-intercept:

    x-intercept(s):

    Domain:

    Range:

    A Cartesian coordinate system is shown with a grid. The horizontal x-axis ranges from -10 to 10, with integer markings. The vertical y-axis also ranges from -10 to 10, with integer markings. The x and y axes intersect at the origin (0, 0).

Answer the following.

  1. The Apollo’s Chariot is a rollercoaster at Busch Gardens with a top speed of 117 km/hr. Its initial (and tallest) descent can be modeled by [latex]h\left(t\right)=52-4.9t^2[/latex], where h is in meters and t is in seconds. How long does it take to reach the bottom of the hill?
  2. Create a quadratic equation with solutions [latex]x=\pm\sqrt5[/latex]
  3. Revisit problem 1, and expand on your previous answer using what you have practiced over solving and graphing in this section.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

College Algebra for Non-STEM Majors Copyright © by Northwest Vista College Mathematics Department is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book