"

2.5 Solving Equations by Factoring

2.5.1 Prep

A. Factor the polynomials using the greatest common factor (GCF) or grouping method.

  1. [latex]10y^2+10[/latex]
  2. [latex]3t^2+6t[/latex]
  3. [latex]15x^2-21x^5[/latex]
  4. [latex]24x^4+30x^7[/latex]
  5. [latex]6x^2-24x+30[/latex]
  6. [latex]8x^3+12x^2-10x[/latex]
  7. [latex]15xz+20x+6yz+8y[/latex]
  8. [latex]24x^3-42x^2+20x-35[/latex]
  9. [latex]3x^2y-6x^2-3xy+6x[/latex]
  10. [latex]30x^2+9xy-20x-6y[/latex]
  11. [latex]56x^2+24xy-70x-30y[/latex]
  12. [latex]8xy+12x-10y-15[/latex]

B. Factor the trinomials completely.

  1. [latex]x^2-6x+8[/latex]
  2. [latex]x^2-14x-15[/latex]
  3. [latex]x^2+3x-28[/latex]
  4. [latex]x^2-6x+9[/latex]
  5. [latex]x^2+3x-10[/latex]
  6. [latex]x^2-2x-15[/latex]
  7. [latex]7x^2-42x+35[/latex]
  8. [latex]3x^2+6x-24[/latex]
  9. [latex]6x^2+x-2[/latex]
  10. [latex]5x^2-14x+8[/latex]
  11. [latex]9x^2+9x-10[/latex]
  12. [latex]7x^2+16x-9[/latex]
  13. [latex]8x^2+6x-9[/latex]
  14. [latex]10x^2+19x+7[/latex]
  15. [latex]3x^2-5x-2[/latex]
  16. [latex]12x^2+x-6[/latex]

C. Factor the binomials completely.

  1. [latex]x^2-49[/latex]
  2. [latex]4x^2-81[/latex]
  3. [latex]x^2+9[/latex]
  4. [latex]32x^3-2x[/latex]
  5. [latex]25x^2+100[/latex]
  6. [latex]49-x^2[/latex]
  7. [latex]x^3-x[/latex]
  8. [latex]3x^3-12x[/latex]

2.5.2 Preview

Example

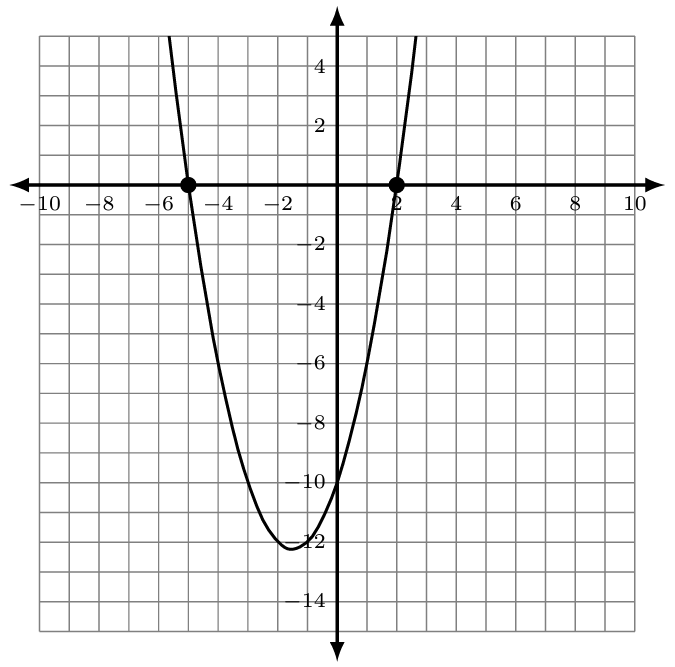
The graph of [latex]f\left(x\right)=x^2+3x-10[/latex] is shown. Notice that the x-intercepts occur at [latex]\left(-5,0\right)[/latex] and [latex]\left(2,0\right)[/latex]. We can use the x-intercepts to write the factored form of this quadratic function by moving the x-intercept over to the other side.

[latex]\begin{array}{rclcccc}x&=&-5&&&&&&&&&&x&=&2\\[1em]x+5&=&-5+5&&&&&&&&&&x-2&=&2-2\\[1em](x+5)&=&0&&&&&&&&&&(x-2)&=&0\end{array}[/latex]

Multiply the factors and combine like terms.

[latex]\begin{array}{rcl}0&=&(x+5)(x-2)\\0&=&x^2-2x+5x-10\\0&=&x^2+3x-10\\f(x)&=&x^2+3x-10\end{array}[/latex]

A parabola is graphed on a Cartesian coordinate system. The x-axis ranges from -10 to 10, and the y-axis ranges from -14 to 6, with integer markings. The parabola opens upwards, with its vertex at approximately (-1.5, -12). It intersects the y-axis at approximately (0, -10) and the x-axis at (-5, 0) and (2, 0).

Example

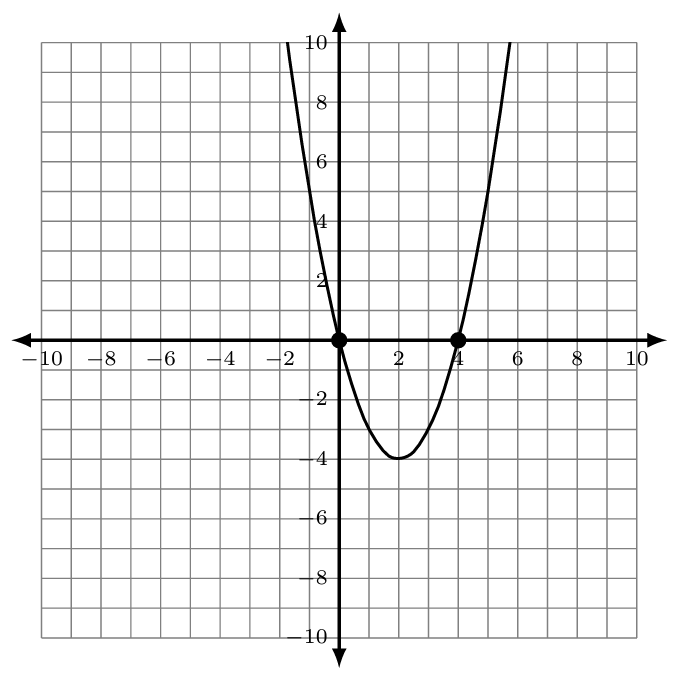
The graph of [latex]f\left(x\right)=x^2-4x[/latex] is shown. Notice that the x-intercepts occur at [latex]\left(0,0\right)[/latex] and [latex]\left(4,0\right)[/latex]. We can use the x-intercepts to write the factored form of this quadratic function.

[latex]\begin{array}{rclcccc}x&=&0&&&&&&&&&&x&=&4\\[1em]x-0&=&0-0&&&&&&&&&&x-4&=&4-4\\[1em]x&=&0&&&&&&&&&&(x-4)&=&0\end{array}[/latex]

Multiply the factors and combine like terms.

[latex]\begin{array}{rcl}0&=&x(x-4)\\0&=&x^2-4x\\f(x)&=&x^2-4x\end{array}[/latex]

A parabola is graphed on a Cartesian coordinate system. The x-axis ranges from -10 to 10, and the y-axis ranges from -10 to 10, with integer markings. The parabola opens upwards, with its vertex at (2, -4). It intersects the y-axis at (0, 0) and the x-axis at (0, 0) and (4, 0).

Try It!

Sketch a possible graph for the quadratic function given in factored form.

[latex]f\left(x\right)=\left(x-5\right)\left(x+2\right)[/latex]

A Cartesian coordinate system is shown with a grid. The horizontal x-axis and the vertical y-axis intersect at the origin. Arrows on the ends of the axes. The grid provides a framework for plotting points and graphs.

Try It!

Sketch a possible graph for the quadratic function given in factored form.

[latex]f\left(x\right)=\left(x+6\right)\left(x-6\right)[/latex]

A Cartesian coordinate system is shown with a grid. The horizontal x-axis and the vertical y-axis intersect at the origin. Arrows on the ends of the axes. The grid provides a framework for plotting points and graphs.

Example

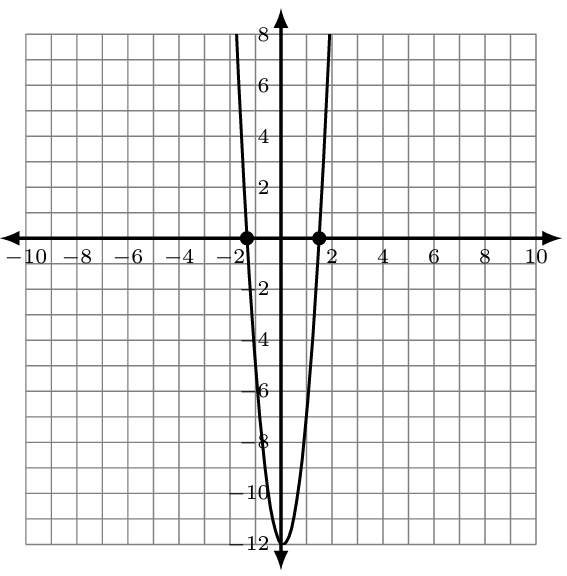
The graph of [latex]f\left(x\right)=6x^2-x-12[/latex] is shown. The x-intercepts occur at [latex]\left(\frac32,0\right)[/latex] and [latex]\left(-\frac43,0\right)[/latex]. We can the x-intercepts to write the factored form of this quadratic function.

[latex]\begin{array}{rclcccc}x&=&\frac32&&&&&&&&&&x&=&-\frac43\\[1em]2⋅x&=&\cancel2⋅\frac3{\cancel2}&&&&&&&&&&3⋅x&=&\cancel3\cdot\left(-\frac4{\cancel3}\right)\\[1em]2x&=&3&&&&&&&&&&3x&=&-4\\[1em]2x-3&=&3-3&&&&&&&&&&3x+4&=&-4+4\\[1em](2x-3)&=&0&&&&&&&&&&(3x+4)&=&0\end{array}[/latex]

 

Multiply the factors and combine like terms

[latex]\begin{array}{rcl}0&=&(2x-3)(3x+4)\\0&=&6x^2+8x-9x-12\\f(x)&=&6x^2-x-12\end{array}[/latex]

A parabola is graphed on a Cartesian coordinate system. The x-axis ranges from -10 to 10, and the y-axis ranges from -12 to 8, with integer markings. The parabola opens upwards, with its vertex at (0, -12). It intersects the y-axis at (0, -12) and the x-axis at (-4/3, 0) and (3/2, 0).

2.5.3 Classwork

A. Solve using the Zero Factor Property.

  1. [latex]9x^2-16=0[/latex]
  2. [latex]x^2+8x+16=9[/latex]
  3. [latex]2x^2+5=2-7x[/latex]
  4. [latex]\frac{x^2}9+1=\frac{2x}3[/latex]
  5. [latex]20x^2+4x^3+25x=0[/latex]
  6. [latex]2t^2+18t+36=0[/latex]
  7. [latex]10x^2=5x[/latex]
  8. [latex]\frac{x^2}5+\frac x4=\frac3{10}[/latex]
  9. [latex]25x^2+45x+8=0[/latex]
  10. [latex]3x^2-12=0[/latex]
  11. [latex]\frac12x^2-32=0[/latex]
  12. [latex]16t^2=49[/latex]
  13. [latex]6=11x-4x^2[/latex]
  14. [latex]15x^2+43x+30=0[/latex]
  15. [latex]2x^2=3x+35[/latex]
  16. [latex]6t^2+7t-24=0[/latex]
  17. [latex]12x^2-32x-75=0[/latex]
  18. [latex]30x^3-2x^2-4x=0[/latex]
  19. [latex]4x^2-31x=-21[/latex]
  20. [latex]80x^3-60x^2-90x=0[/latex]
  21. [latex]15t^2-t-2=0[/latex]
  22. [latex]12x^2+x=6[/latex]
  23. [latex]7x^2-23x+6=0[/latex]
  24. [latex]6x^2+25x+4=0[/latex]
  25. [latex]\frac{9x^2}{16}-\frac19=0[/latex]
  26. [latex]\frac14x^2=1[/latex]

B. Graph and identify the following characteristics for the function.

    1. [latex]g\left(x\right)=2x^2+8x[/latex]

      Opens: Up / Down

      Axis of Symmetry:

      Vertex:

      y-intercept:

      x-intercept(s):

      Domain:

      Range:

      A Cartesian coordinate system is shown with a grid. The horizontal x-axis ranges from -10 to 10, with integer markings. The vertical y-axis also ranges from -10 to 10, with integer markings. The x and y axes intersect at the origin (0, 0).

C. Answer the following.

  1. The height h (in feet) of a small rocket t seconds after it is launched is given by the function [latex]h\left(t\right)=-16t^2+128t.[/latex]
    1. How long is the rocket in the air?
    2. When is the rocket 112 feet high?
  2. Use the equation [latex]3x^2+9x=0[/latex] to answer the following.
    1. Solve using the Quadratic Formula.
    2. Solve using the Zero Factor Property.
    3. Discuss the differences between (a) and (b). State which method you prefer and why.
  3. Spot the error and correct it.[latex]4x^2+12x+9=0[/latex][latex]4(x^2+12x+9)=0[/latex]

2.5.4 Homework

A. Solve using the Zero Factor Property.

  1. [latex]x^2+8x+15=0[/latex]
  2. [latex]4t^2-25=0[/latex]
  3. [latex]6x^2-x=15[/latex]
  4. [latex]10x^2+100x=0[/latex]
  5. [latex]4t^2+12t+9=0[/latex]
  6. [latex]4x^2=23x+6[/latex]
  7. [latex]x^2+\frac{16}9=\frac83x[/latex]
  8. [latex]\frac12x^2-\frac56x-2=0[/latex]
  9. [latex]x^3+4x^2-12x=0[/latex]
  10. [latex]\frac32x^2+3x+\frac43=0[/latex]
  11. [latex]20x^2-4x=0[/latex]
  12. [latex]\frac29t^2+t+1=0[/latex]
  13. [latex]5t^2-23t+12=0[/latex]
  14. [latex]36x^3=81x[/latex]
  15. [latex]6x-4x^3=23x^2[/latex]
  16. [latex]5-2x^2-3x=0[/latex]
  17. [latex]4x^2-x[/latex]
  18. [latex]2x^2-50[/latex]
  19. [latex]\frac52t^2-\frac13t-\frac43=0[/latex]
  20. [latex]\frac13x^2+\frac7{12}x=\frac58[/latex]
  21. Give an equation you prefer to solve using the Zero Factor Property. Give an equation you prefer to solve by the Quadratic Formula.

B. Graph and identify the following characteristics for the function.

  1. [latex]m\left(x\right)=-x^2+1[/latex]

    Opens: Up / Down

    Axis of Symmetry:

    Vertex:

    y-intercept:

    x-intercept(s):

    Domain:

    Range:

    A Cartesian coordinate system is shown with a grid. The horizontal x-axis ranges from -10 to 10, with integer markings. The vertical y-axis also ranges from -10 to 10, with integer markings. The x and y axes intersect at the origin (0, 0).

C. Answer the following.

  1. A rocket carrying fireworks is launched from a hill above a lake. The rocket will fall into lake after exploding at its maximum height. The rocket’s height above the surface of the lake is given by [latex]h\left(t\right)=-16t^2+64t+80[/latex], where h is in feet and t is in seconds.
    1. How long will it take for the rocket to hit 128 feet?
    2. After how many seconds after it is launched will the rocket hit the lake?
  2. Fill in the blank to create an equation that may solved using the Zero Factor Property.

    [latex]x^2+\_\_\_\_\_\_\_\_\_\_\_\_\_\_\;x-12=0[/latex]

  3. Explain in your own words how to solve the following equation using the Zero Factor Property. Be sure to explain why you perform each step.

    [latex]x^2+12x+20=4x+5[/latex]

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

College Algebra for Non-STEM Majors Copyright © by Northwest Vista College Mathematics Department is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book