"

Linear Relationships and Functions

Prep for Percent and Proportion

  1. [latex]\frac18[/latex]
  2. [latex]\frac38[/latex]
  3. [latex]\frac68;\;\text{equivalent}\;\text{to}\;\frac34[/latex]
  4. [latex]\frac26[/latex]
  5. [latex]\frac23[/latex]
  6. [latex]\frac34;\;\text{equivalent}\;\text{to}\;\frac68[/latex]
  7. [latex]1\frac23[/latex]
  1. Answers may vary.
  2. It is necessary to write 1 if it is the part (not the whole) in a ratio.
  1. Part = 8; Whole = 22.58; Fraction [latex]=\frac8{22.58}[/latex]
  2. Part = 58; Whole = 82; Fraction [latex]=\frac{58}{82}[/latex]
  3. Part = 4,630; Whole = 15,435; Fraction [latex]=\frac{4,630}{15,435}[/latex]
  4. Part = 212; Whole = 802; Fraction [latex]=\frac{212}{802}[/latex]
  5. Part = 170; Whole = 950; Fraction [latex]=\frac{170}{950}[/latex]
  6. Part = [latex]2\frac12[/latex]; Whole = [latex]5\frac34[/latex]; Fraction [latex]=\frac{2{\displaystyle\frac12}}{5{\displaystyle\frac34}}[/latex]
    1. subtraction
    2. multiplication
    3. division
    4. addition
    5. multiplication
    6. addition (-7) or subtraction (7)
    7. division
    8. multiplication
    9. multiplication and division
    10. multiplication
    11. multiplication and division
    12. multiplication and division
    1. subtraction
    2. subtract 5 from both sides; [latex]x=14[/latex]
    3. [latex]x=55[/latex]
    1. addition
    2. add 5 to both sides; [latex]x=7[/latex]
    3. [latex]x=42[/latex]
    1. division
    2. divide both sides by 3; [latex]x=21[/latex]
    3. [latex]x=22[/latex]
    1. No. [latex]x-3[/latex] is held by subtraction;
      [latex]-3x[/latex] is held by multiplication
    2. add 3 to both sides; [latex]x=15[/latex]
    3. divide both sides by [latex]-3;x=-4[/latex]
    1. division
    2. multiplication
    3. multiply both sides by 4; [latex]x=60[/latex]
    4. [latex]x=100[/latex]
  7. multiplication, division; division, multiplication; [latex]x=25[/latex]
  8. multiplication; [latex]x=\frac15[/latex]
  9. [latex]x=20[/latex]
  1. [latex]p=0.1[/latex]
  2. [latex]n=150[/latex]
  3. [latex]x=5200[/latex]
  4. [latex]x=17.5[/latex]
  5. [latex]x=21[/latex]
  6. [latex]x=56[/latex]
  7. [latex]t=20.4[/latex]
  8. [latex]x=4[/latex]
  9. [latex]x=3[/latex]
  10. [latex]b=8[/latex]

Classwork: Percent and Proportion

  1. Explain.
  2. Explain.
  1. 70
  2. 17.5%
  3. 62.5
  4. 130
  5. [latex]233.\overline3[/latex]
  6. 555 students
  7. 3.6%
  8. 6.97%
  9. 66 beats
  10. 800 calories
  11. 105.86 gallons
  12. $209,300
  13. $21.22
  14. $1966.67
  15. 62% decrease
  16. 25% increase
  17. 2 gal of 50%; 4 gal of 75%
  18. 4 cups; 5%
  19. [latex]3\frac14[/latex] cups of 2.77% fat
  20. 35 pints; 5% salinity
  21. 5 liters of 1%; The mixture is 1.57%
  22. [latex]\approx0.96\%[/latex]
  23. 2,250 people
  24. 1,600 trout
  25. $44.56
  26. [latex]\approx67.07\%[/latex]
  27. 52 games

Homework: Percent and Proportion

  1. [latex]10.08[/latex]
  2. [latex]92[/latex]
  3. [latex]\approx31.48\%[/latex]
  4. [latex]3.12[/latex]
  5. Explain.
  6. 1,234 students
  7. [latex]\approx71.4\%[/latex]
  8. An equation in which two ratios (fractions) are set equal
  9. Cross multiply and solve for the unknown
  1. [latex]t=20.4[/latex]
  2. [latex]x=4[/latex]
  3. [latex]x=3[/latex]
  4. [latex]k=3[/latex]
  5. [latex]b=8[/latex]
  6. 3.75 miles
  7. [latex]$219,000[/latex]
  8. [latex]3\frac13[/latex] hours
  9. 3,750 penguins
  10. 2.1 lbs
  11. 462 lbs
  12. 7,700 lbs
  13. 165 calories
  14. 19 ft
  15. 35 puppies, 20 adult dogs
  16. 630 frat men
  17. 51.3% are females
  18. [latex]$369.52[/latex]
  19. $9.90 discount, $23.09 sale price
  20. $92.81 tax, $1,217.81
  21. $7.00 tip
  22. 49% decrease
  23. Explain
  24. 4,000 gallons; 2.625% salinity
  25. [latex]2\frac12[/latex] cup of 4% fat
  26. [latex]1\frac34[/latex] cups; 1.7% alcohol
  27. 3 quarts of whole milk; the mixture is 5.8% fat
  28. liters of 1% low-fat; 1.8% fat in the mixture

Prep for Scientific Notation and Conversions

  1. [latex]10[/latex]
  2. [latex]100[/latex]
  3. [latex]10,000[/latex]
  4. [latex]10,000,000[/latex]
  5. Discussion may vary
  6. [latex]10^4[/latex]
  7. [latex]10^8[/latex]
  1. [latex]0.1[/latex]
  2. [latex]0.01[/latex]
  3. [latex]0.0001[/latex]
  4. [latex]0.0000001[/latex]
  5. Discussion may vary.
  6. [latex]10^{-5}[/latex]
  7. [latex]10^{-9}[/latex]
  8. [latex]700[/latex]
  9. [latex]0.0003[/latex]
  10. [latex]7,450,000[/latex]
  11. [latex]0.000314[/latex]

Classwork: Scientific Notation and Metric Conversions

Scientific Notation

  1. [latex]3.54\times10^7[/latex]
  2. [latex]9.876\times10^{-9}[/latex]
  3. [latex]2,320,000[/latex]
  4. [latex]0.0052[/latex]

Metric System Conversions

  1. [latex]0.5[/latex] m
  2. [latex]8,000[/latex] g
  3. [latex]9100[/latex] L
  4. [latex]98[/latex] mg
  5. [latex]0.0091[/latex] L
  6. [latex]720,000[/latex] mm
  7. [latex]568,000[/latex] mg
  8. [latex]98,000[/latex] µg
  9. [latex]2,000,000[/latex] µg
  10. [latex]40,000[/latex] cm2
  11. [latex]250,000,000[/latex] cm3
  12. [latex]130,400[/latex] km2

Homework: Scientific Notation and Metric Conversions

  1. [latex]3.04\times10^3[/latex]
  2. [latex]-4.789\times10^{-3}[/latex]
  3. [latex]7.18\times10^{-6}[/latex]
  4. [latex]3.108\times10^{6}[/latex]
  5. Many answers are possible.
    1. [latex]2.5\times10^{-3}[/latex]
    2. [latex]2.5[/latex] mg
    3. [latex]2500[/latex] µg
    4. Discuss.
  2. [latex]5\times10^2[/latex] mL
  3. [latex]1.6\times10^2[/latex] mm
  4. [latex]1.04\times10^7[/latex] cm
  5. [latex]4.8\times10^2[/latex] cm2
  6. [latex]1.98\times10^{-3}[/latex] kg
  7. [latex]2.5\times10^{-2}[/latex] km
  8. [latex]1.6\times10^5[/latex] mm3
  9. [latex]1.2\times10^{-5}[/latex] ML
  10. France by [latex]136,033[/latex] km2

Prep for Imperial Conversions

  1. [latex]90[/latex]
  2. [latex]19.3548[/latex]
  3. [latex]12,096[/latex]
  4. [latex]\frac{5}{8}[/latex] or 0.625
  5. Compare with a classmate
  1. [latex]\frac{\cancel8}1\cdot\frac5{\cancel8}=5[/latex]
  2. [latex]\frac{\cancel{4.5}}1\cdot\frac7{\cancel{4.5}}=7[/latex]
  3. [latex]\frac{\cancelto{2}{10}}{1} \cdot \frac{3}{\cancel5} = 6[/latex]
  4. [latex]\frac{\cancelto{2}{12}}{1} \cdot\frac{\bcancel5}{\cancel6}\cdot\frac7{\bcancel5}=14[/latex]
  5. [latex]\frac{15}{\cancel8}\cdot\frac{\cancel8}{\bcancel7}\cdot\frac{\bcancel7}4=\frac{15}4[/latex]
  6. [latex]\frac91\cdot\frac21\cdot\frac{11}1=198[/latex]
  7. [latex]\frac{\cancel9}1\cdot\frac{10}{\cancel3}\cdot\frac5{\cancel3}=50[/latex]
  8. [latex]\frac{\cancel{25}}4\cdot\frac2{\cancel5}\cdot\frac2{\cancel5}=1[/latex]
  9. [latex]72[/latex] yd
  10. [latex]74[/latex] feet
  11. [latex]64[/latex] m2
  12. [latex]312[/latex] ft2
  13. [latex]125[/latex] in3
  14. [latex]936[/latex] ft3
  15. 1; 2 (square units); 3 (cubic units)
Length (distance)
1 dimension		 Area
2 dimensions		 Volume
3 dimensions		 Mass Time Imperial (British) Metric
1. cm ✓ ✓
2. cm3 ✓ ✓
3. in2 ✓ ✓
4. g ✓ ✓
5. hm ✓ ✓
6. dag ✓ ✓
7. years ✓ ✓
8. dL ✓ ✓
9. dam2 ✓ ✓
10. mm3 ✓ ✓
11. m ✓ ✓
12. mi ✓ ✓
  1. [latex]\frac{2.54\;cm}{1\;\text{in}},\;\text{length}[/latex]
  2. [latex]\frac{12\;\text{in}}{1\;ft},\;\text{length}[/latex]
  3. [latex]\frac{0.3048\;m}{1\;ft},\;\text{length}[/latex]
  4. [latex]\frac{640\;\;\text{acres}}{1\;mi^2},\;\text{area}[/latex]
  5. [latex]\frac{0.001\;m^3}{1L},\;\text{volume}[/latex]
  6. [latex]\frac{3\;ft}{1yd},\;\text{length}[/latex]
  7. [latex]\frac{9\;ft^2}{1yd^2},\;\text{area}[/latex]
  8. [latex]\frac{29.5735\;cm^3}{1\;oz},\;\text{volume}[/latex]

Classwork: Imperial Conversions

  1. Answers may vary.
  2. Answers may vary.
  3. 2 yds
  4. 54.61 cm
  5. 131.23 yd
  6. 88,513.92 m
  7. [latex]8.0645[/latex] cm2
  8. [latex]46,609.2[/latex] ft2
  9. 13056 oz
  10. 6 lbs
  11. [latex]864[/latex] in3
  12. 259,200 sec
  13. 6 years 3.34 months
  14. 120 mi/day
  15. 272.19 L/hr
  16. [latex]2.998\times10^8[/latex] m/sec
  17. Discuss with a classmate.

Applications of Conversions

  1. [latex]1.58\times10^9[/latex] sec
  2. [latex]226.04[/latex] ft2
  3. [latex]2.58[/latex] sec
  4. [latex]1,728[/latex] in
  5. [latex]15,840[/latex] in2
  6. [latex]7.33[/latex] ft/s
  7. Mat’s bathtub fills faster
  8. 7 lb, 10.05 oz

Homework: Imperial Conversions

  1. [latex]6.21[/latex] mi
  2. [latex]120,000,000[/latex] µg
  3. [latex]12,672[/latex] ft
  4. [latex]109.68[/latex] cm2
  5. [latex]804.4[/latex] mL
  6. [latex]2[/latex] ft
  7. [latex]10.57[/latex] pt
  8. [latex]25.4[/latex] cm
  9. [latex]20[/latex] lb
  10. [latex]525,600[/latex] min
  11. [latex]131.234[/latex] yd
  12. [latex]66,908,160[/latex] ft2
  13. [latex]23,562[/latex] in3
  14. [latex]5,297.2[/latex] ft3
  15. [latex]4.299[/latex] lb
  16. [latex]42.33[/latex] oz
  17. [latex]4.23[/latex] pt
  18. [latex]220.98[/latex] m
  19. [latex]25.1[/latex] gal
  20. [latex]26.82[/latex] m/s
  21. [latex]5.93\times10^{-6}[/latex] m3
  22. [latex]0.0283[/latex] m3
  23. [latex]14.2[/latex] mg/mm2
  24. [latex]82.4[/latex] mg/mm2
  1. [latex]6.214[/latex] miles
  2. Explain.
    1. No
    2. Explain.
    3. 27.8 mph
  4. [latex]290.8[/latex] mph
  5. [latex]750[/latex] mph
  6. [latex]320,544[/latex] in/wk
  7. [latex]{5.407\times10}^{-4}[/latex] kg/s
      1. centimeters
  9. [latex]452.23[/latex] km
  10. 7 lb, 11 oz
  11. [latex]\approx[/latex] 54 yr, 9.5 months
  12. 31.7 years old
    1. 300 feet and
    2. 91,744 cm
  14. The gallon size because it is $0.02/oz.
  15. [latex]125,840[/latex] ft
  16. 53 days
  17. Houston by 419.58 km2
  18. [latex]3.73\times10^{17}[/latex] m3; [latex]3.73\times10^{20}[/latex] liters
  19. 31,709.8 years old
  20. 946,352.9 pages
  21. 187.96 cm
  22. 3 ft
  23. 20.86 in
  24. 25.4 kg
  25. 4 times
  26. 4.93 mL
  27. 14.79 mL
  28. 12.25 lbs, 5.56 kg
  29. 160 oz
  30. 4731.76 mL
  31. 2.464 cc
  32. 0.125 qt
  33. 50000 µg
  34. 2.5 cc
  35. 6 tsp

Prep: Linear Graphs - Intercepts Method

    1. I and IV; I and III
    2. I and II; III and IV
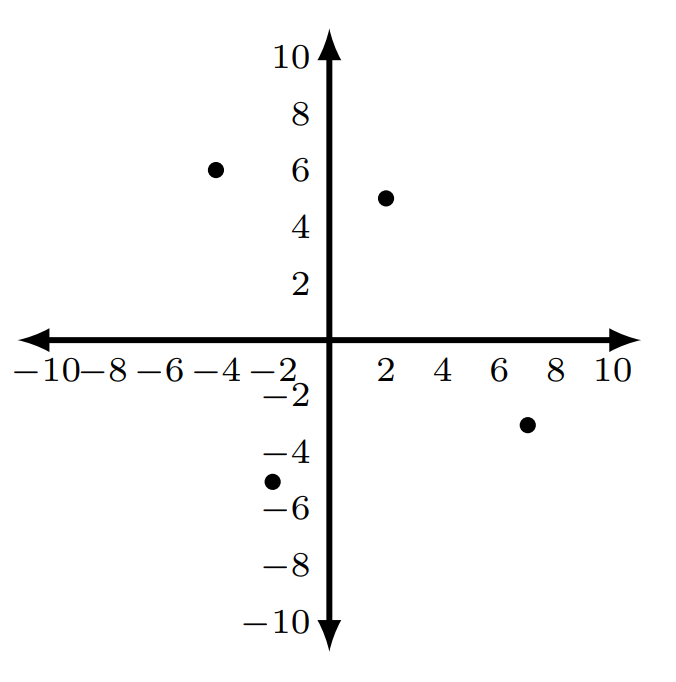
  1. A Cartesian coordinate plane with both x- and y-axes labeled from -10 to 10. The graph shows four plotted points: one in the second quadrant at (-5, 6), one in the first quadrant at (2, 5), one in the fourth quadrant at (7, -3), and one in the third quadrant at (-2, -5).
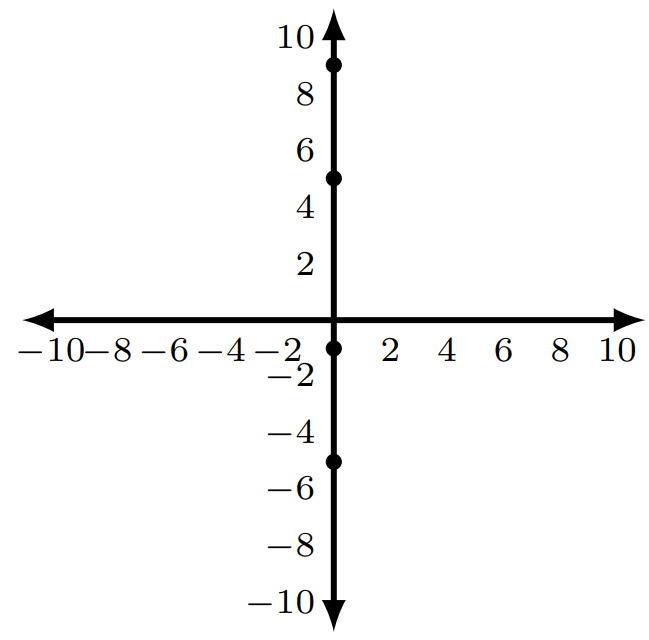
    1. A Cartesian coordinate plane with x- and y-axes labeled from -10 to 10. Four equally spaced black points are plotted along the y-axis at (0, -5), (0, -1), (0, 5), and (0, 9). The x-axis contains no plotted points.
    2. They lie on the y-axis.
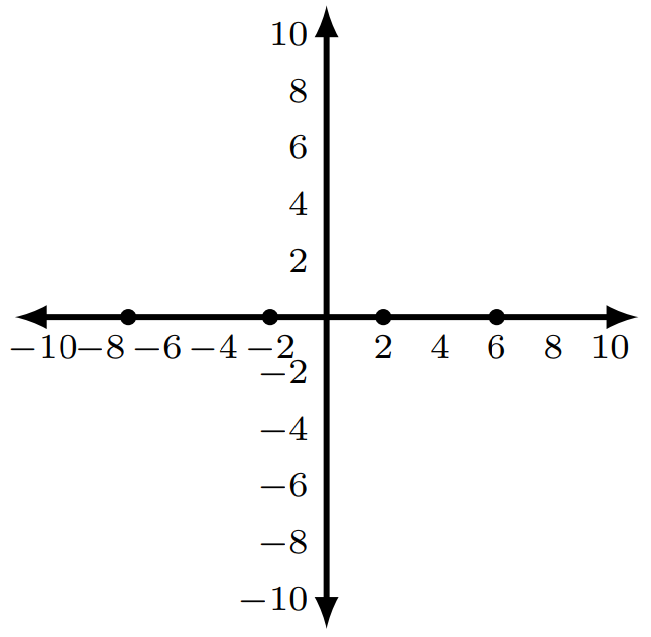
    1. A Cartesian coordinate plane with x- and y-axes labeled from -10 to 10. The x-axis contains four points positioned at (-8, 0), (-2, 0), (4, 0), and (6, 0). The y-axis has no plotted points
    2. They lie on the x-axis.

Classwork: Intercepts Method

  1. y-intercept: [latex](0, 9)[/latex]; x-intercept: [latex](\frac{9}{2}, 0)[/latex]
  2. y-intercept: [latex](0, 6)[/latex]; x-intercept: [latex](-6, 0)[/latex]
  3. y-intercept: [latex](0, \frac{1}{2})[/latex]; x-intercept: [latex](-3, 0)[/latex]
  4. y-intercept: [latex](0, \frac{17}{5})[/latex]; x-intercept: [latex](\frac{17}{8}, 0)[/latex]
  5. Answers may vary.
  6. y-intercept: [latex](0, 4)[/latex]; x-intercept: none
  7. y-intercept: none; x-intercept: [latex](-2, 0)[/latex]
  8. Answers may vary.
  1. y-intercept: [latex](0, 5)[/latex]; x-intercept: [latex](2, 0)[/latex]
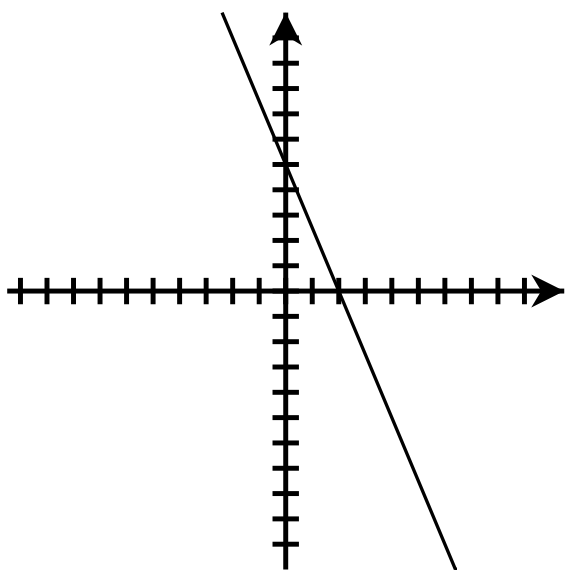
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A straight line with a negative slope passes through the points (0, 5) on the y-axis and (2, 0) on the x-axis. The line descends from left to right.
  2. y-intercept: [latex](0, 2)[/latex]; x-intercept: [latex](-4, 0)[/latex]
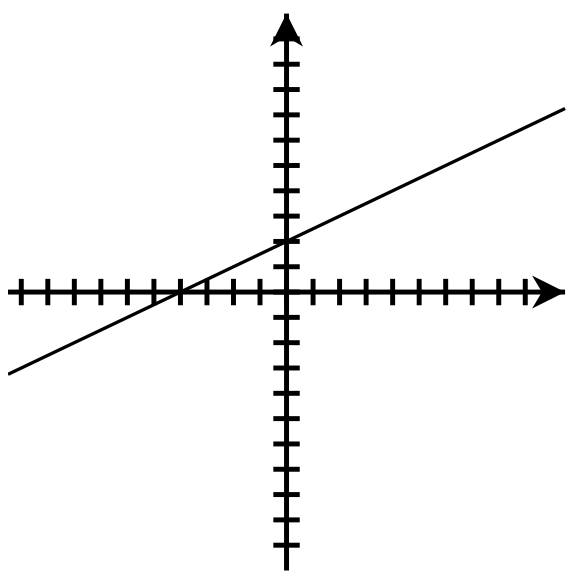
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A straight line with a positive slope passes through the points (-4, 0) on the x-axis and (0, 2) on the y-axis, rising from left to right.
  3. y-intercept: [latex](0, -1)[/latex]; x-intercept: [latex](-8, 0)[/latex]
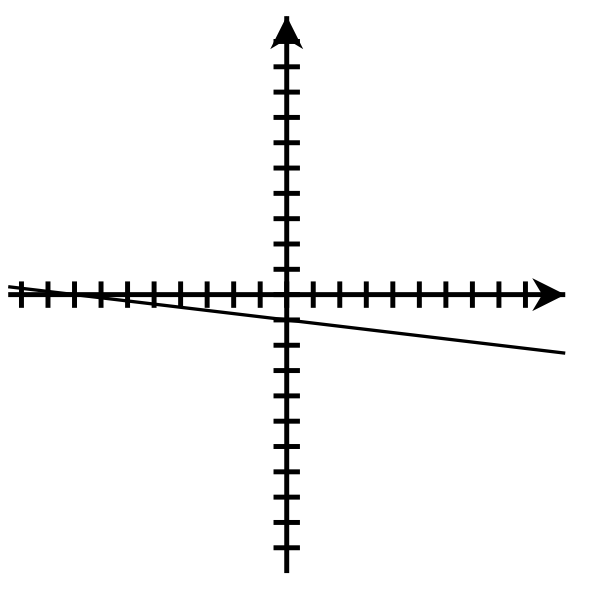
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A straight line with a negative slope passes through the points (-8, 0) on the x-axis and (0, -1) on the y-axis, descending gently from left to right.
  4. y-intercept: [latex](0, \frac{1}{3})[/latex]; x-intercept: [latex](-3, 0)[/latex]
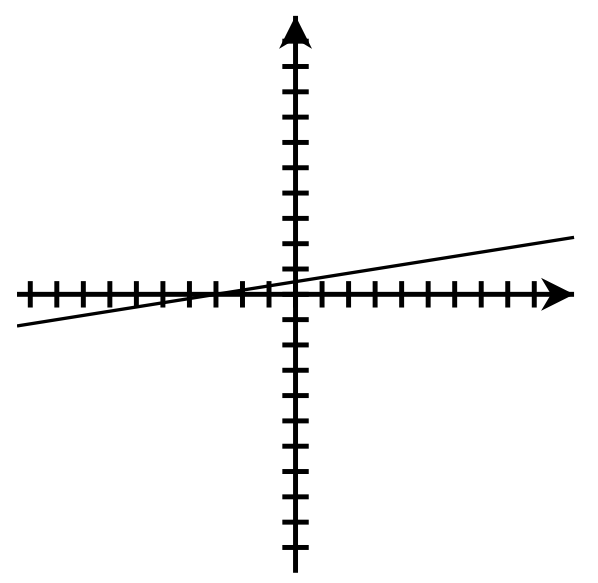
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A straight line with a gentle positive slope passes through the points (-3, 0) on the x-axis and (0, 1/3) on the y-axis, rising gradually from left to right.
  5. y-intercept: [latex](0, 4)[/latex]; x-intercept: none
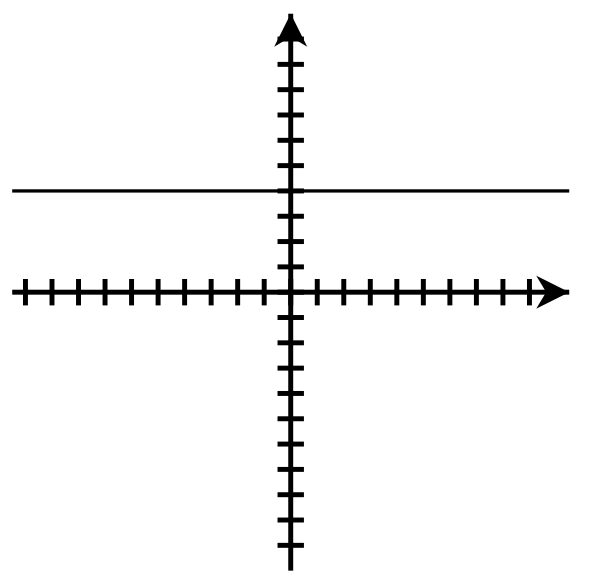
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A horizontal line passes through the y-axis at (0, 4) and extends parallel to the x-axis across the graph.
  6. y-intercept: none; x-intercept: [latex](-2, 0)[/latex]
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A vertical line passes through the point (-2, 0) on the x-axis and extends parallel to the y-axis across the graph.

Homework: Intercepts Method

  1. Answers may vary.
  2. Answers may vary.
  1. y-intercept: [latex](0, 8)[/latex]; x-intercept: [latex](\frac{8}{3}, 0)[/latex]
  2. y-intercept: [latex](0, -2)[/latex]; x-intercept: [latex](6, 0)[/latex]
  3. y-intercept: [latex](0, \frac{2}{3})[/latex]; x-intercept: [latex](-\frac{1}{2}, 0)[/latex]
  4. y-intercept: [latex](0, -3)[/latex]; x-intercept: none
  1. y-intercept: [latex](0, -2)[/latex]; x-intercept: [latex](6, 0)[/latex]
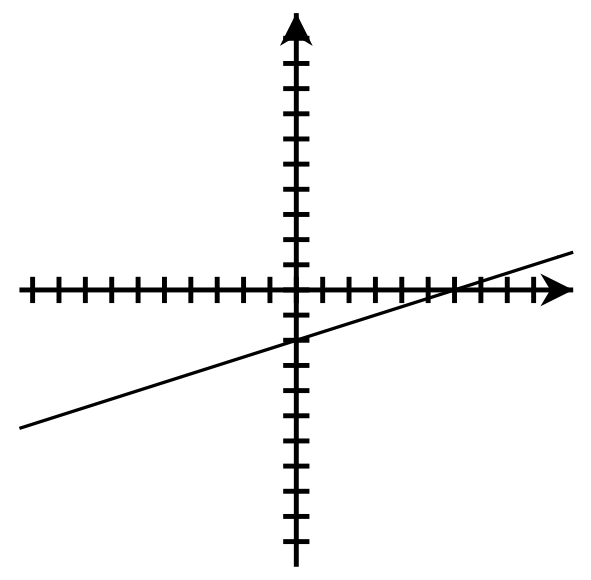
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A straight line with a positive slope passes through the points (0, -2) on the y-axis and (6, 0) on the x-axis, rising from left to right.
  2. y-intercept: [latex](0, -1)[/latex]; x-intercept: [latex](3, 0)[/latex]
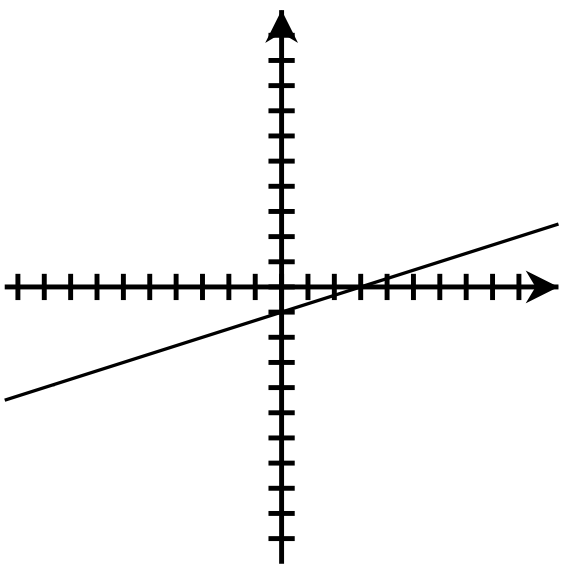
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A straight line with a positive slope passes through the points (0, -1) on the y-axis and (3, 0) on the x-axis, rising from left to right.
  3. y-intercept: [latex](0, 3)[/latex]; x-intercept: [latex](9, 0)[/latex]
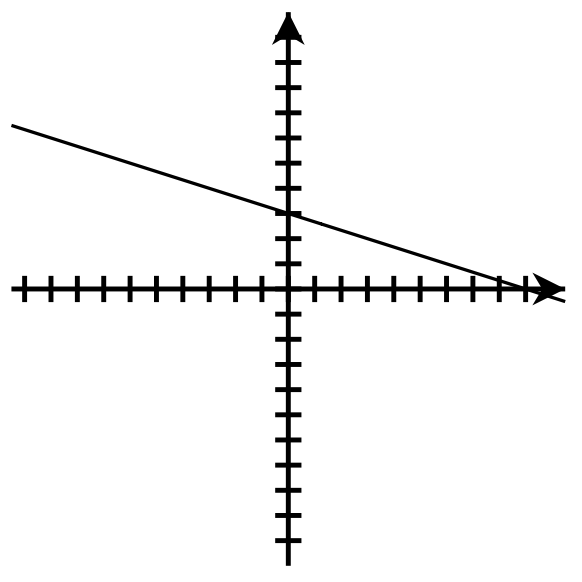
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A straight line with a negative slope passes through the points (0, 3) on the y-axis and (9, 0) on the x-axis, descending from left to right.
  4. y-intercept: none; x-intercept: [latex](4, 0)[/latex]
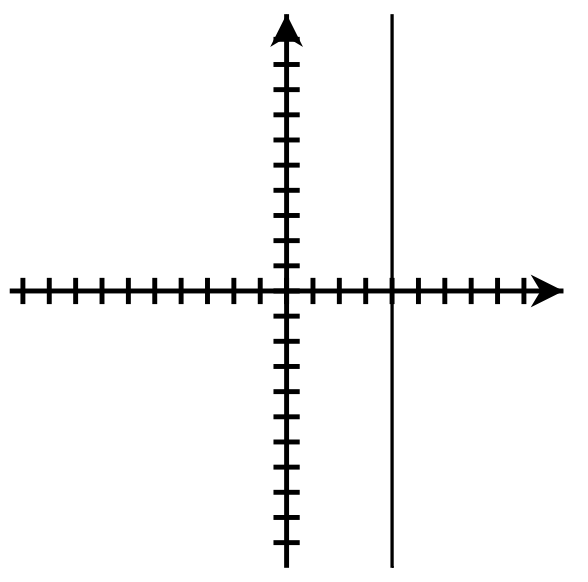
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A vertical line passes through the point (4, 0) on the x-axis and extends parallel to the y-axis across the graph.
  1. Answers may vary.
  2. Discuss with a classmate.
    1. [latex](0,-6)[/latex]
    2. [latex](0,-6)[/latex]
    3. Explain.
  4. Explain.
  5. Explain.

Prep: Linear Graphs - Slope-Intercept Method

  1. [latex]y = \frac{3}{2}x + 4[/latex]
  2. [latex]y = -x + 3[/latex]
  3. [latex]y = -\frac{2}{3}x + 5[/latex]
  4. [latex]y = x - 3[/latex]
  5. [latex]y = -2x - 1[/latex]
  6. [latex]y = -\frac{1}{3}x - 1[/latex]
  7. [latex]y = 2x - 6[/latex]
  8. [latex]y = \frac{3}{4}x - 6[/latex]
  9. [latex]y = -\frac{1}{4}x + 3[/latex]
  10. [latex]y = -x - 6[/latex]
  11. [latex]y = \frac{1}{6}x - \frac{1}{3}[/latex]
  12. [latex]y = -\frac{2}{3}x + 4[/latex]
  1. [latex]3[/latex]
  2. [latex]-\frac12[/latex]
  3. [latex]-\frac{12}7[/latex]
  4. [latex]-\frac{29}{28}[/latex]
  5. [latex]0[/latex]
  6. Undefined
  7. Discuss with classmates.

Classwork: Slope-Intercept Method

  1. [latex]y = \frac{3}{2}x + 4[/latex];
    [latex]m = \frac{3}{2}[/latex]; y-intercept: [latex](0, 4)[/latex]
  2. [latex]y = -x + 3[/latex];
    [latex]m = -1[/latex]; y-intercept: [latex](0, 3)[/latex]
  3. [latex]y = -\frac{2}{3}x + 5[/latex];
    [latex]m = -\frac{2}{3}[/latex]; y-intercept: [latex](0, 5)[/latex]
  4. [latex]y = 2x - 3[/latex];
    [latex]m = 2[/latex]; y-intercept: [latex](0, -3)[/latex]
  5. [latex]y = -4[/latex];
    [latex]m = 0[/latex]; y-intercept: [latex](0, -4)[/latex]
  6. [latex]x = 16[/latex];
    m is undefined; y-intercept: none
  7. [latex]y = \frac{1}{6}x - \frac{1}{3}[/latex];
    [latex]m = \frac{1}{6}[/latex]; y-intercept: [latex](0, -\frac{1}{3})[/latex]
  8. [latex]y = \frac{3}{4}x - 6[/latex];
    [latex]m = \frac{3}{4}[/latex]; y-intercept: [latex](0, -6)[/latex]
  9. Answers may vary.
  10. Many answers possible.
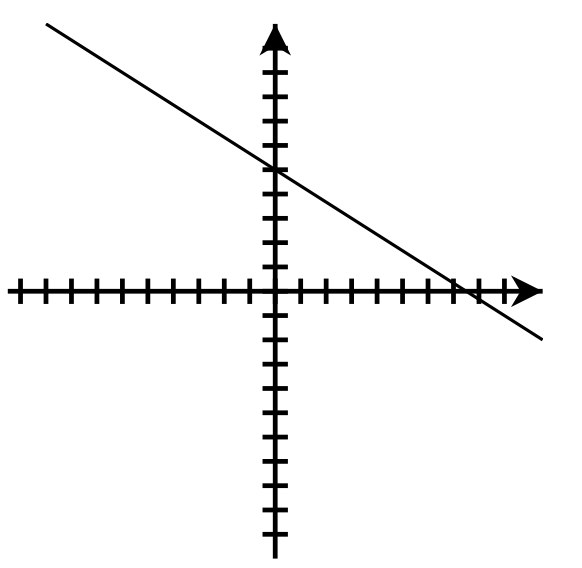
  1. [latex]y = -\frac{2}{3}x + 5[/latex];
    [latex]m = -\frac{2}{3}[/latex]; y-intercept: [latex](0, 5)[/latex]
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A straight line with a negative slope of -2/3 passes through the point (0, 5) on the y-axis and descends from left to right.
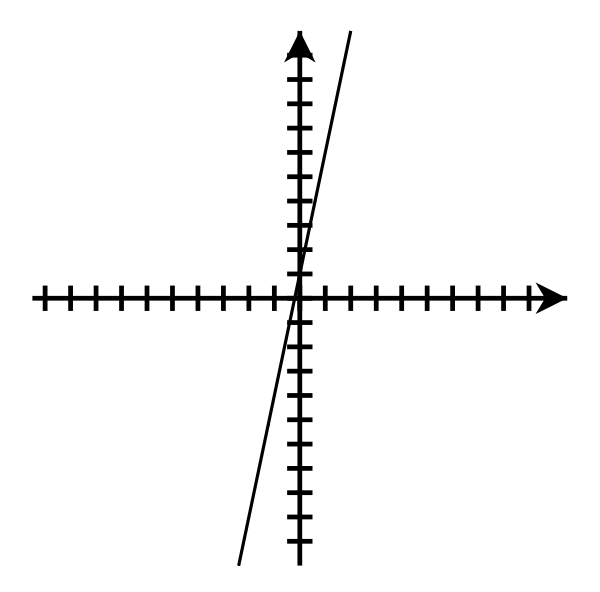
  2. [latex]y = 5x + 1[/latex];
    [latex]m = 5[/latex]; y-intercept: [latex](0, 1)[/latex]
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A straight line with a steep positive slope of 5 passes through the point (0, 1) on the y-axis and rises sharply from left to right.
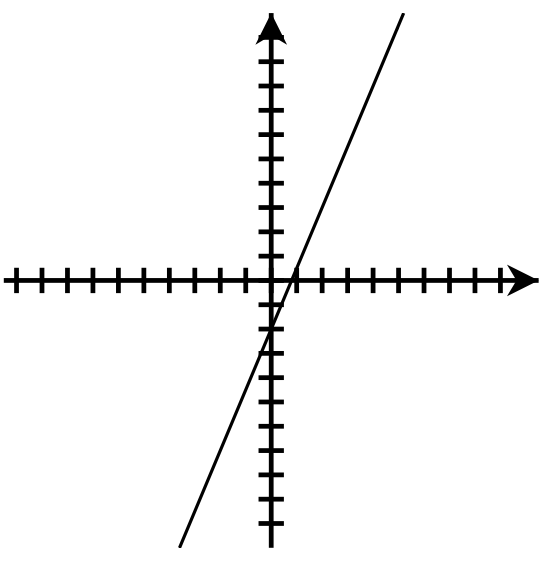
  3. [latex]y = \frac{5}{2}x - 2[/latex];
    [latex]m = \frac{5}{2}[/latex]; y-intercept: [latex](0, -2)[/latex]
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A straight line with a positive slope of 5/2 passes through the point (0, -2) on the y-axis and rises sharply from left to right.
  4. [latex]y = \frac{1}{2}x - \frac{4}{3}[/latex];
    [latex]m = \frac{1}{2}[/latex]; y-intercept: [latex](0, -\frac{4}{3})[/latex]
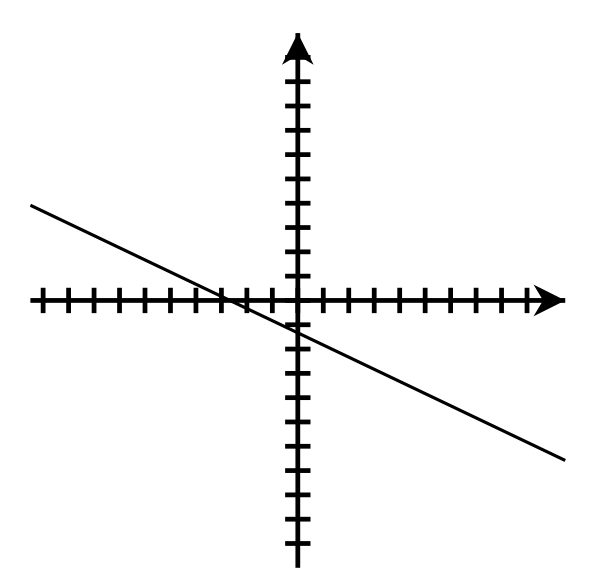
  5. [latex]y = 4x[/latex];
    x-intercept: [latex](0, 0)[/latex]; y-intercept: [latex](0, 0)[/latex]. Use the slope to find another point.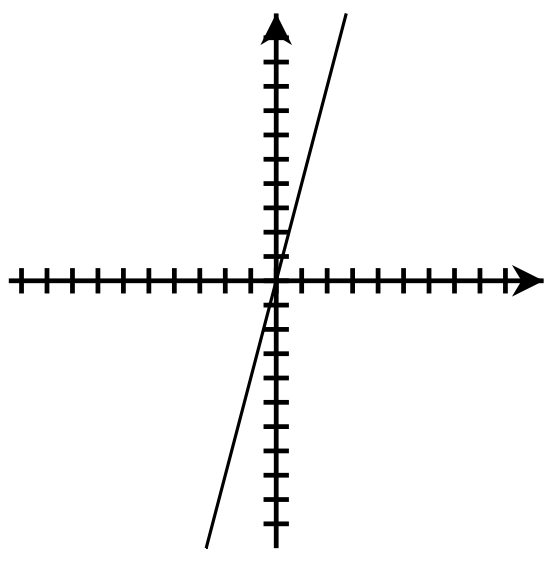A Cartesian coordinate plane with evenly spaced tick marks along both axes. A straight line with a steep positive slope representing y=4x passes through the point (0, 0) and rises sharply from left to right.
  6. Compare your answers with your classmates.
  1. [latex]m = -\frac{1}{2}[/latex]
  2. [latex]m = -2[/latex]
  3. [latex]m = -\frac{3}{8}[/latex]
  4. [latex]m = \frac{96}{35}[/latex]
  5. [latex]m = 0[/latex]
  6. m is undefined

Parallel and Perpendicular Lines

    1. [latex]m = -\frac{2}{5}[/latex]
    2. [latex]m = -\frac{2}{5}[/latex]
    3. The slopes are equal;
      their graphs are parallel.
    1. [latex]m = \frac{1}{3}[/latex]
    2. [latex]m = -3[/latex]
    3. The slopes are negative reciprocals;
      their graphs are perpendicular.

Homework: Slope-Intercept Method

  1. [latex]y = -\frac{12}{25}x + 12[/latex];
    [latex]m = -\frac{12}{25}[/latex]; y-intercept: [latex](0, 12)[/latex]
  2. [latex]y = \frac{1}{3}x - 3[/latex];
    [latex]m = \frac{1}{3}[/latex]; y-intercept: [latex](0, -3)[/latex]
  3. [latex]y = -x + 4[/latex];
    [latex]m = -1[/latex]; y-intercept: [latex](0, 4)[/latex]
  4. [latex]y = -\frac{1}{4}x - \frac{2}{3}[/latex];
    [latex]m = -\frac{1}{4}[/latex]; y-intercept: [latex](0, -\frac{2}{3})[/latex]
  5. [latex]y = \frac{3}{4}x - \frac{15}{2}[/latex];
    [latex]m = \frac{3}{4}[/latex]; y-intercept: [latex](0, -\frac{15}{2})[/latex]
  6. [latex]y = -3[/latex];
    [latex]m = 0[/latex]; y-intercept: [latex](0, -3)[/latex]
  1. Answers may vary.
  2. Explain.
  1. [latex]m = -\frac{3}{2}[/latex]; y-intercept: [latex](0, -5)[/latex]
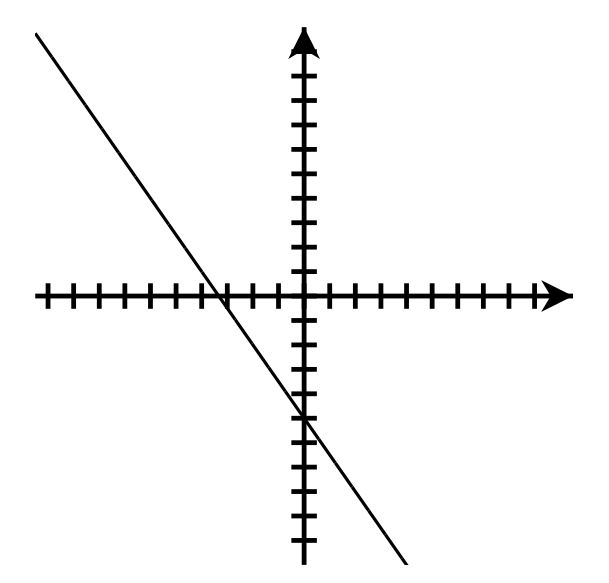
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A straight line with a negative slope of -3/2 passes through the point (0, -5) on the y-axis and descends from left to right.
  2. [latex]y = -\frac{1}{3}x + 3[/latex];
    [latex]m = -\frac{1}{3}[/latex]; y-intercept: [latex](0, 3)[/latex]
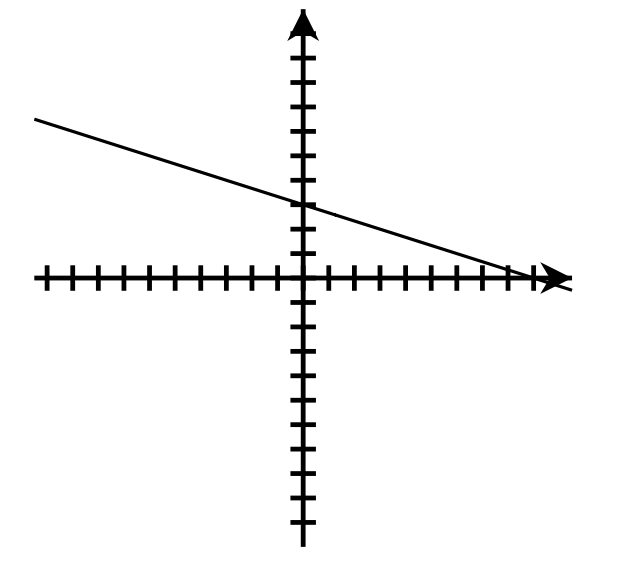
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A straight line with a negative slope of -1/3 passes through the point (0, 3) on the y-axis and descends gradually from left to right.
  3. [latex]y = \frac{1}{4}x - 3[/latex];
    [latex]m = \frac{1}{4}[/latex]; y-intercept: [latex](0, -3)[/latex]
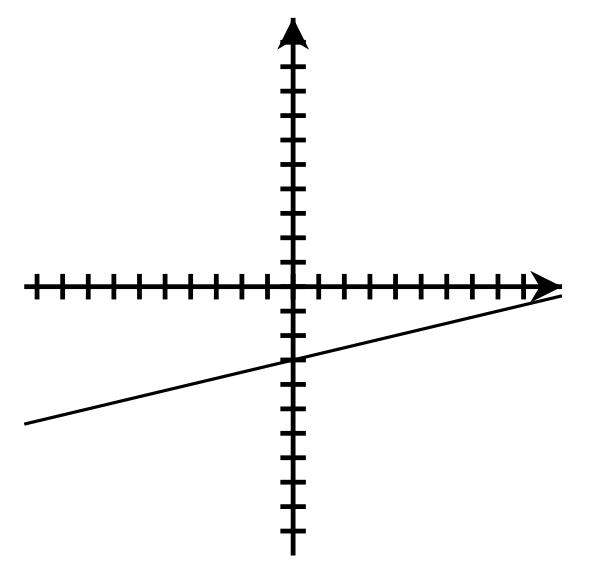
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A straight line with a gentle positive slope of 1/4 passes through the point (0, -3) on the y-axis and rises slowly from left to right.
  4. [latex]y = 2x + 3[/latex];
    [latex]m = 2[/latex]; y-intercept: [latex](0, 3)[/latex]
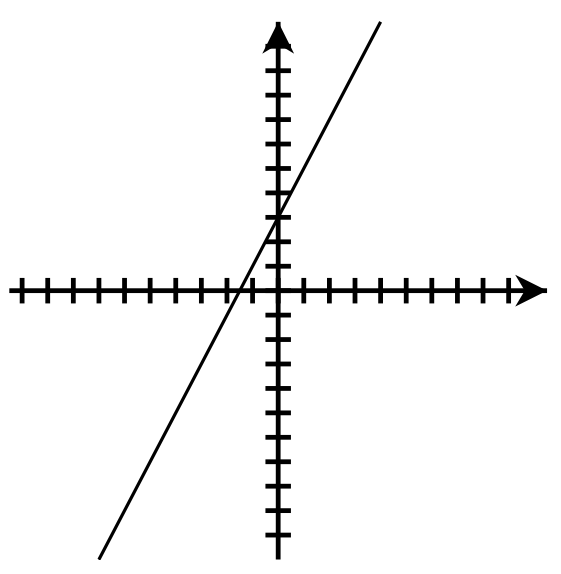
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A straight line with a positive slope of 2 passes through the point (0, 3) on the y-axis and rises steeply from left to right.
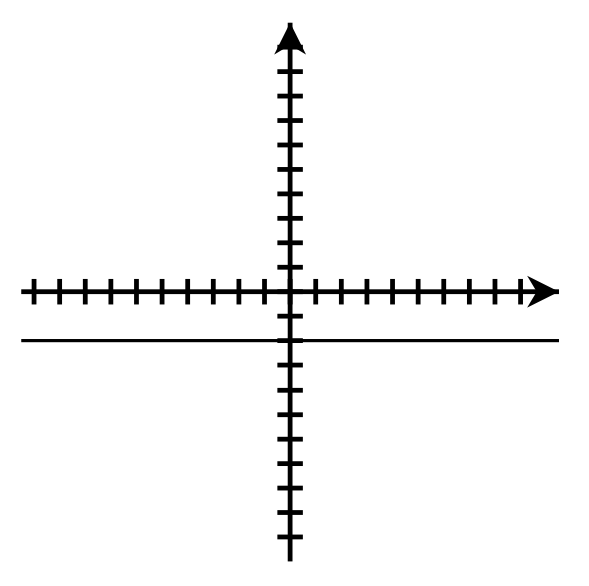
  5. [latex]y = -2[/latex];
    [latex]m = 0[/latex]; y-intercept: [latex](0, -2)[/latex]
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A horizontal line with slope m=0 passes through the point (0, -2) on the y-axis and extends parallel to the x-axis across the graph.
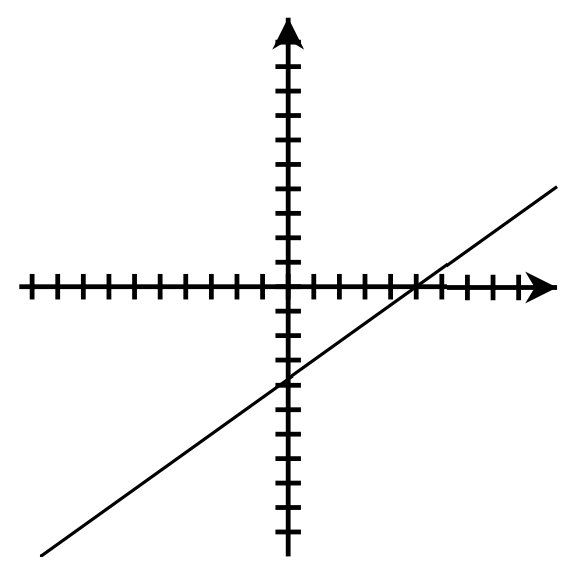
  6. [latex]y = \frac{3}{4}x - \frac{15}{4}[/latex];
    [latex]m = \frac{3}{4}[/latex]; y-intercept: [latex](0, -\frac{15}{4})[/latex]
    A Cartesian coordinate plane with evenly spaced tick marks along both axes. A straight line with a positive slope of 3/4 passes through the point (5, 0) on the x-axis and rises gradually from left to right.
  1. [latex]m = -\frac{1}{3}[/latex]
  2. [latex]m = 1[/latex]
  3. [latex]m = -\frac{11}{9}[/latex]
  4. [latex]m = -\frac{12}{35}[/latex]
  5. [latex]m = -\frac{81}{170}[/latex]
  1. (A) and (C) are parallel; Both (A) and (C) are perpendicular to (B)

Prep: Function Notation and Applications of Linear Functions

  1. [latex]-6[/latex]
  2. [latex]14[/latex]
  3. [latex]\frac{7}{10}[/latex]
  4. [latex]-\frac{13}{16}[/latex]
  5. [latex]-17[/latex]
  6. [latex]147.75[/latex]
  1. [latex]x = \frac{3}{4}[/latex]
  2. [latex]t = 14[/latex]
  3. [latex]x = \frac{13}{30}[/latex]
  4. [latex]x = -\frac{3}{2}[/latex]
  1. Independent: Time (months)
    Dependent: Weight (lb)
    Rate: 4 lbs per month
  2. Independent: Sales ($)
    Dependent: Salary ($)
    Rate: Not given
  3. Independent: Credit hours
    Dependent: Cost ($)
    Rate: $80 per hour
  4. Independent: Number of visits
    Dependent: Cost ($)
    Rate: $4.50 per visit
  5. Independent: Altitude
    Dependent: Temperature
    Rate: Not given
  6. Independent: Time (years)
    Dependent: Meals out
    Rate: Not given

Classwork: Function Notation & Linear Applications

  1. [latex]-32[/latex], input, [latex](-3, -32)[/latex]
  2. [latex]-5[/latex], input, [latex](0, -5)[/latex]
  3. [latex]10[/latex], output, [latex](10, 85)[/latex]
  4. [latex]9a - 5[/latex], input
  5. [latex]1[/latex], input, [latex](\frac{2}{3}, 1)[/latex]
  6. [latex]\frac{5}{9}[/latex], output, [latex](\frac{5}{9}, 0)[/latex]
  1. [latex]4[/latex]
  2. [latex]1[/latex]
  3. [latex]4[/latex]
  4. [latex]0[/latex]
  5. [latex]-6[/latex]
  6. [latex]-1[/latex]
  7. [latex]-3[/latex]
  8. [latex]-4[/latex]
  1. $37.50
  2. Answers will vary by current year.
    1. 260 pounds
    2. 4 pounds per month
    3. 15.5 months
  4. The y-intercept is [latex](0, 20000)[/latex] which means her salary is $20,000 at $0 in sales.
    The slope is [latex]m = 0.3[/latex], which means her salary increases by $0.30 per $1.00 in sales.
    1. Explain
    2. Check with your neighbor
    3. 128 visits
    1. The temperature decreases by 3.5°F per thousand ft. gain in elevation.
    2. 16.6°F
    3. 7,600 feet
  7. 251 meals in 2030
  8. Many answers are possible.
  9. Because the rate of change is not constant
  10. 3 liters of 1% low-fat; 1.8% fat in the mixture

Homework: Function Notation & Linear Applications

  1. [latex]-5[/latex], input, [latex](-3, -5)[/latex]
  2. [latex]23[/latex], input, [latex](4, 23)[/latex]
  3. [latex]\frac{13}{2}[/latex], output, [latex](\frac{13}{2}, 33)[/latex]
  4. [latex]31[/latex], input, [latex](6, 31)[/latex]
  5. [latex]\frac{15}{2}[/latex], input, [latex](\frac{1}{8}, \frac{15}{2})[/latex]
  6. [latex]-\frac{7}{4}[/latex], output, [latex](-\frac{7}{4}, 0)[/latex]
  7. Explain
  8. Discuss.
  1. [latex]f(-2) = 0[/latex]
  2. [latex]f(1) = -1.5[/latex]
  3. [latex]f(4) = 6[/latex]
  4. [latex]f(0) = -6[/latex]
  5. [latex]x = -1.9, 0.6[/latex]
  6. [latex]x = -2.1, 3.4[/latex]
  7. [latex]x = -1[/latex]
  8. [latex]x = -2, 2, 3[/latex]
  9. 66 beats
  10. Answers will vary by current year.
    1. [latex]C(x) = 115x + 1000[/latex]
    2. [latex]C(12) = $2,380[/latex]
    1. $99 is the initial cost
    2. DVR costs $5.99 per month
    3. [latex]C(24) = $242.76[/latex]
    1. Explain
    2. Check with a classmate
    3. 29 miles
    1. $200
    2. $3.00
    3. 200 desserts
    1. [latex]m = -88.2[/latex];
      Credit card debt decreases by $88.20 per year
    2. [latex]D(x) = -88.2x + 7768[/latex]
    3. $5563
  16. 14 gallons of 1% acid; 21 gallons of 2%

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

College Algebra for Non-STEM Majors Copyright © by Northwest Vista College Mathematics Department is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book