Appendices
Linear Equations in One Variable
A. Solve the following equations for the unknown variable. #1-4 are one step equations because you only have undo one operation to isolate the variable.
- [latex]x\;-\;7\;=\;10[/latex]
- [latex]5\;+\;y\;=\;8[/latex]
- [latex]7x\;=\;-21[/latex]
- [latex]-3y\;=\;42[/latex]
-
- Are [latex]-3y\;=\;42[/latex] and [latex]-3\;+\;y\;=\;42[/latex] the same thing? Why or why not?
- How would you solve [latex]-3\;+\;y\;=\;42[/latex]?
- In your words, explain how part (b) was different from solving #4.
- Spot the error! Explain in your own words the mistake made and correct it.
[latex]8x\;=\;4[/latex][latex]\frac{8x}4=\frac44[/latex][latex]x\;=\;2[/latex] - Spot the error! Explain in your own words the mistake made and correct it.
[latex]8x\;=\;4[/latex][latex]\frac{8x}{8x}=\frac4{8x}[/latex][latex]x\;=\;\frac12[/latex]
B. #8-14 are multistep equations because you have undo more than one operation to isolate the variable.
- [latex]2x\;-\;5\;=\;7[/latex]
- [latex]2\;+\;3y\;=\;17[/latex]
- [latex]3\;-\;3x\;=\;9[/latex]
- [latex]1\;-\;y\;=\;-10[/latex]
- [latex]8\;-\;4y\;=\;18[/latex]
- [latex]-2y\;-\;4\;=\;-1[/latex]
- Solve [latex]5\;-\;6y\;=\;-7[/latex] two different ways.
- Start by subtracting 5 from both sides.
- Start by adding 6y to both sides.
- Which way do you prefer and why?
- Spot the errors! Explain in your own words the mistakes made and correct them.
[latex]3\;-\;4x\;=\;-9[/latex]
[latex]3\;-\;4x\;+\;9\;=\;-9\;+\;9[/latex]
[latex]12\;-\;4x[/latex]
[latex]\frac{12}4-\frac{4x}4[/latex]
[latex]x\;=\;3[/latex]
When you see a number held together to an expression by parentheses such as [latex]4(x\;-\;5)[/latex], what operation is implied (addition, subtraction, multiplication, or division)?
The distributive property of multiplication over addition
[latex]a(b\;+\;c)\;=\;a\;\cdot\;b\;+\;a\;\cdot\;c[/latex]
Try it! Simplify the following expressions by distributing.
- [latex]4(x\;-\;5)[/latex]
- [latex]4\left(\frac x4-\frac54\right)[/latex]
- [latex]4\left(\frac12-\frac52y\right)[/latex]
- [latex]12\left(\frac x4-\frac53\right)[/latex]
When you see an expression held together by a fraction bar such as [latex]\frac{x-6}3[/latex], what operation is implied (addition, subtraction, multiplication, or division)?
And how can you undo this operation?
Try it! Clear the following equations of the fractions and then solve.
- [latex]\frac{x-6}3=\frac13[/latex]
- [latex]\frac x4-\frac54=\frac14[/latex] What if the denominators are not all the same number?
- [latex]\frac x2-\frac34=3[/latex]
- [latex]\frac x4-\frac53=1[/latex]
- [latex]\frac12-\frac23y=4[/latex]
- [latex]\frac12-\frac{5y}2=\frac34[/latex] What if the variable shows up on both sides of the equation?
- [latex]8x\;+\;9\;=\;7x\;-\;3[/latex]
- [latex]6(3\;+\;x)\;=\;5(x\;+\;1)[/latex]
- [latex]\frac3{1+x}=2[/latex]
- [latex]\frac{28+x}{7+x}=2[/latex]
Fractions
Try It!
To visualize and better understand the multiplication
[latex]\frac34\cdot\frac18[/latex]
try the following.
- Take a piece of notebook paper and fold it hot dog style, then fold it hot dog style again. Open and see how the paper has 4 sections. Shade the 3 of the 4 sections using this pattern: ////
- Take the same sheet of paper and fold it hamburger style, then repeat folding the top to the bottom 2 more times. Open and see how the paper made 8 sections. Shade one 1 of the 8 sections using this pattern:\\\\\\\\
- How many sections have both the //// and \\\\\\\\ shading? Out of how many? (Notice that this is what multiplying fractions represents: a piece of a piece.)
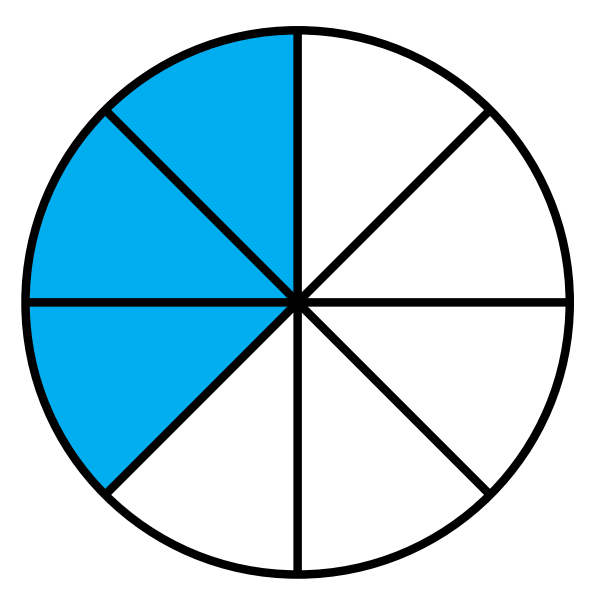
Example. The shaded portion of each of the following circles represent the fractions [latex]\frac38[/latex] and [latex]\frac34[/latex], respectively.
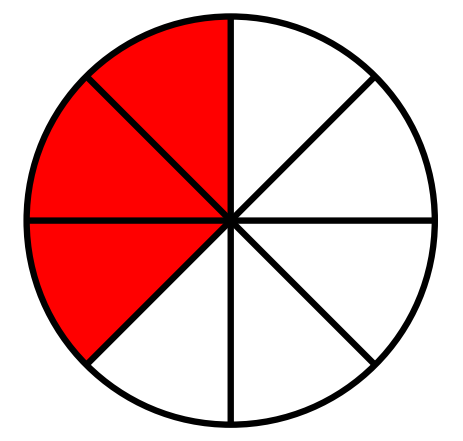
Try It!
- Draw a circle whose shaded portion represents the fraction [latex]\frac12[/latex].
- Draw a circle whose shaded portion represents the fraction [latex]\frac13[/latex].
- Notice that the number of slices in each circle you drew above are different. How would you add together the two shaded portions when the number of slices of in each circle is not the same? Demonstrate using your circles from part (a) and (b).
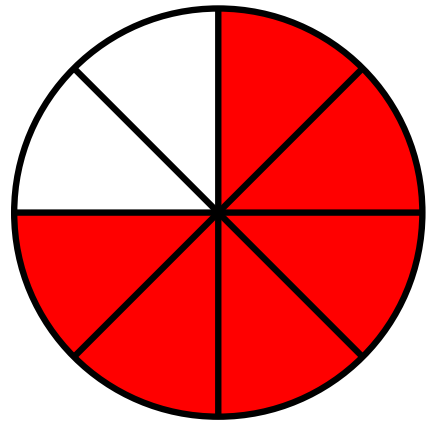
Example
The sum of the shaded portions of each of the following circles represents the mixed number [latex]1\frac38[/latex] which is the same as the improper fraction [latex]\frac{11}8[/latex]
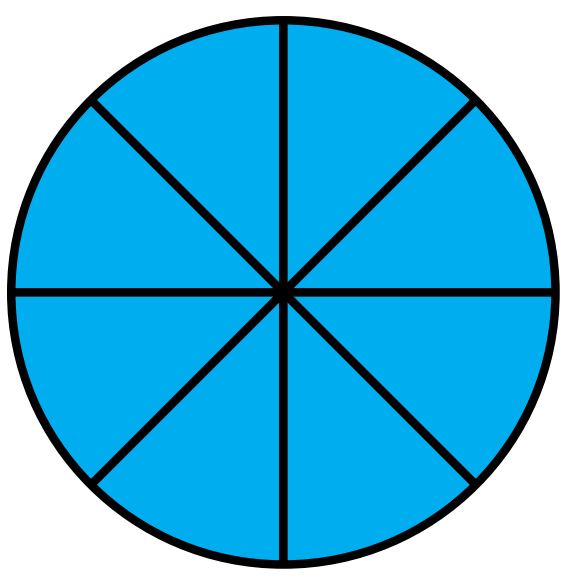
Classwork: Fractions
- How would you visually depict each of the following?
- [latex]\frac{1}{2} \cdot \frac{2}{3}[/latex]
- [latex]\frac{1}{6} + \frac{4}{6}[/latex]
- [latex]\frac{5}{8} - \frac{1}{4}[/latex]
-
- [latex]\frac{4}{9} \cdot \frac{3}{16}[/latex]
- [latex]\frac{7}{8} \div \frac{2}{9}[/latex]
- [latex]\frac{21}{24} \cdot \frac{16}{18}[/latex]
- [latex]\frac{4}{9} \div \frac{42}{18}[/latex]
- [latex]\frac{4}{5} \cdot \frac{1}{8}[/latex]
- [latex]1 \frac{4}{9} \div 2 \frac{1}{4}[/latex]
- [latex]\frac{1}{8} + \frac{2}{5}[/latex]
- [latex]7 \frac{3}{5} - \frac{1}{2}[/latex]
- [latex]\frac{5}{9} - \frac{1}{6}[/latex]
- [latex]\frac{2}{9} + \frac{2}{3}[/latex]
-
- [latex]\frac{2}{3} \cdot \frac{12}{19} = \frac{24}{57}[/latex]
- [latex]\frac{4}{5} + \frac{2}{3} = \frac{6}{8} = \frac{3}{4}[/latex]
- [latex]1 \frac{2}{3} - \frac{4}{5} = -1 \frac{2}{5}[/latex]
- [latex]2 \frac{1}{3} \div \frac{4}{5} = \frac{7}{3} \div \frac{4}{5} = \frac{3}{7} \cdot \frac{4}{5} = \frac{12}{35}[/latex]
Applications with Fractions
- Solve.
- Dolores sold candy by the pound. The first person who came into her store bought [latex]2\frac{1}{4}[/latex] pounds of gumdrops. The second person who came into the store bought [latex]5\frac{3}{4}[/latex] pounds of jelly beans. How many pounds of candy did Dolores sell to her first two customers?
- In Language Arts the class was assigned to write a team paper. Each team was to write [latex]5\frac{1}{2}[/latex] pages for the combined paper. When all the teams put their papers together, there were a total of [latex]44[/latex] pages. How many teams had worked on this paper?
- Dennis’s new dog weighs [latex]127\frac{3}{4}[/latex] pounds. His friend’s dog weighs [latex]94\frac{1}{2}[/latex] pounds. How much more does Dennis’s dog weigh than his friend’s dog?
- On their vacation trip last summer the Pace family got [latex]30\frac{1}{2}[/latex] miles per gallon of fuel on their trip from home. On the return trip they only got [latex]17\frac{7}{8}[/latex] miles per gallon. How many more miles per gallon of fuel did they get on their way out than on their way home?
- Jerry bought [latex]12\frac{1}{2}[/latex] pounds of candy to share with his friends. If he gave [latex]2\frac{1}{2}[/latex] pounds each to three friends, how much candy does he have left?
- Joy and her friend wanted to do something different. They decided to go to the track and see how many times they could run around the track without stopping. When they finally finished, their stopwatch showed they each ran a total of [latex]23\frac{2}{5}[/latex] minutes. If on average Joy also knew it took them [latex]4\frac{1}{2}[/latex] minutes to run around the track once, how many times did they make it around the track?
Homework: Fractions
- Perform the operation
- [latex]\frac{3}{8} + \frac{3}{8}[/latex]
- [latex]5\frac{3}{8} + 2\frac{7}{8}[/latex]
- [latex]\frac{5}{9} + \frac{1}{3}[/latex]
- [latex]7\frac{5}{6} - 2\frac{3}{10}[/latex]
- [latex]\frac{2}{7} \cdot \frac{3}{5}[/latex]
- [latex]10 - 5\frac{4}{9}[/latex]
- [latex]\frac{5}{12} + \frac{7}{8}[/latex]
- [latex]7\frac{1}{3} - 3\frac{6}{7}[/latex]
- [latex]11\frac{1}{3} \div 4\frac{1}{2}[/latex]
- [latex]12\frac{7}{9} + 3\frac{11}{12}[/latex]
- [latex]\frac{7}{9} - \frac{1}{6}[/latex]
- [latex]5\frac{1}{3} \div 2\frac{1}{4}[/latex]
- [latex]3\frac{1}{2} \cdot 4\frac{2}{3}[/latex]
- [latex]8\frac{2}{5} - 4\frac{3}{4}[/latex]
- [latex]4\frac{2}{5} + 2\frac{1}{5}[/latex]
- [latex]4 - 1\frac{7}{8}[/latex]
- Find the errors and correct them.
- [latex]\frac{3}{4} + \frac{1}{2} = \frac{4}{6} = \frac{2}{3}[/latex]
- Solve.
- Deb had [latex]4\frac{3}{4}[/latex] yards of leopard print fabric. She wanted to make a skirt that called for [latex]2\frac{7}{8}[/latex] yards of fabric. How much will she have left over?
- Traci bought [latex]1 \frac{1}{4}[/latex] yards of yellow ribbon, [latex]2 \frac{5}{6}[/latex] yards of pink ribbon and [latex]3 \frac{1}{2}[/latex] yards of purple ribbon. How many yards of ribbon did she buy altogether?
- Emily is buying [latex]\frac25[/latex] pounds of beans for dinner. Ricky is buying [latex]\frac74[/latex] of the amount of beans that Emily is buying. How many pounds of beans is Ricky buying? Express your answer in simplest form.
- How much chocolate will each person get if 3 people share [latex]\frac12[/latex] pound of chocolate equally?
- How many [latex]\frac34[/latex] cup servings are in [latex]\frac23[/latex] of a cup of yogurt?
- Sheila was making cupcakes for the school parent-student dinner. Sheila knew that she had put in [latex]13\frac23[/latex] ounces of ingredients she had to mix together in the blender. After she was finished, she poured the mix into [latex]2\frac14[/latex] ounce cupcake tins. How many of these cupcakes would one batch of this mix make? How much of the mix would be left over?
- One day Mr. Saunders walked [latex]4\frac12[/latex] miles to one store and [latex]2\frac15[/latex] miles to another store. Then he walked [latex]7\frac56[/latex] miles again to a third store. How far did he end up walking altogether?
- For one of their Science experiments, a class used [latex]10\frac12[/latex] quarts of water. If there were 7 groups doing the experiment and each group used the same amount of water, how any quarts of water did each group use?
- Robert and his father raked up [latex]17\frac14[/latex] bags of leaves from their yard. Robert’s father has a machine that shreds the leaves to almost nothing. If Robert has already thrown in [latex]8\frac12[/latex] bags, how many more does he have to throw in to shred them all?
Order of Operations
- Simplify the expressions.
- [latex]5 - 3 + 72(10 - 2)[/latex]
- [latex]2 + 2(3 - 6) - (1 + (1 - 4)^2)[/latex]
- [latex]\sqrt{5^2 - 3^2}[/latex]
- [latex]|4 - 8| - 9 \cdot (2 - 3)[/latex]
- [latex]\frac{7^3 + 2(4)}{17 - 3}[/latex]
- [latex]1 + \frac{\frac{2}{5} + \frac{1}{3}}{2^3}[/latex]
- [latex]-3(5 + 1)^2[/latex]
- [latex]48 \div 3 \cdot 2 - 4^2 + 5[/latex]
- [latex]\frac{(4 + 3 \cdot 2) + (3 \cdot -1)}{-1^2}[/latex]
- [latex]\frac{\frac{3}{5} + \frac{1}{3}}{2^3}[/latex]
- [latex]3 + 2(4 + (-6)) + (1 + (-2)^2)[/latex]
- [latex]2(4 - |-5|) - (1 + 4)^2[/latex]
- [latex]\frac{1}{2} \cdot 8 \div 6[/latex]
- [latex]\frac{2}{5} + \frac{4}{3} \div 2[/latex]
- [latex](\frac{1}{2})^2 + \frac{1}{5}[/latex]
Solving Linear Equations
- Solve the equations.
- [latex]5(x - 2) = 4x - 10[/latex]
- [latex]2x - 5x = 3(2x - 4)[/latex]
- [latex]10x + (4 - x) = 7x + 2(3x + 5)[/latex]
- [latex]3 - (2 - 7x) = 2x - (-5x - 1)[/latex]
- [latex]\frac{3(t - 7)}{2} = t - 6[/latex]
- [latex]\frac{6}{7} + x = \frac{13}{7}[/latex]
- [latex]\frac{(x - 2)}{3} = x - 1[/latex]
- [latex]\frac{2}{5}x - \frac{5}{7}x = x - 1[/latex]
- [latex]10x - (4 - 3x) = 7x + 2(3x + 5)[/latex]
- [latex]4 - \frac{1}{3}(2 - 7x) = 2(x - 1)[/latex]
- [latex]\frac{4(x + 9)}{3} = x[/latex]
- [latex]\frac{6}{11} + x = \frac{11}{7}[/latex]
Linear Expressions and Equations
- Simplify or solve.
- [latex]\frac{x}{3} + \frac{1}{4}x - 1[/latex]
- [latex]\frac{x}{3} + \frac{1}{4}x = 1[/latex]
- [latex]\frac{x}{4} + 3x[/latex]
- [latex]5x - (x - 3) = 7 + 2(x + 6)[/latex]
- [latex]\frac{3(x - 3)}{2} -x[/latex]
- [latex]\frac{3(x - 3)}{2} = x[/latex]
Homework: Order of Operations and Linear Equations
- Simplify the expressions.
- [latex]5 - (7 - 3)[/latex]
- [latex]\sqrt{16} - 3[/latex]
- [latex](8 + 7)5[/latex]
- [latex]\frac{7}{10} + (-\frac{2}{3})[/latex]
- [latex]\frac{10 - 6}{9 - 7}[/latex]
- [latex](\frac{1}{3})(-6)^2 + 3[/latex]
- [latex]-7(2) + 8(\frac{1}{2}) - \sqrt{25}[/latex]
- [latex]\frac{(5 + 3 \cdot 5) + 3(-1)}{(-1)^2}[/latex]
- [latex](\frac{1}{5} + \frac{6}{5})^2[/latex]
- [latex]\frac{\frac{7}{8} - \frac{1}{9}}{3}[/latex]
- [latex]\frac{(\frac{2}{7})^2}{\frac{2}{21}}[/latex]
- [latex]\frac{(\frac{1}{3} - \frac{3}{4})^2}{\frac{2}{3}}[/latex]
- [latex]\frac{\frac{2}{3} - \frac{1}{4}}{\frac{2}{5} + \frac{1}{4}} \div 2[/latex]
- [latex]\frac{1}{3} + \frac{(\frac{1}{2} - \frac{3}{4})^2}{(-\frac{1}{2})^2}[/latex]
- [latex]\frac{(\frac{1}{4} - \frac{2}{3})^2}{2^3} + \frac{1}{2} \div \frac{3}{8}[/latex]
- Solve the equations
- [latex]\frac{x}{-2} = -9[/latex]
- [latex]6x + 5x = -31 - 2[/latex]
- [latex]-3(4 - x) = 12[/latex]
- [latex](7x - 5) - (x - 4) + (3x - 8) = 3x - 5[/latex]
- [latex]8.54x - 5.71x + 3.8x = -39.78[/latex]
- [latex]5(x + 2) - \frac{2}{3}x + \frac{x}{2} = 6x - 11[/latex]
- [latex]-9x - 1 + 7x = -3 - 10[/latex]
- [latex]7 - x = 10[/latex]
- [latex]36 = (5c + 4) - (2c + 4)[/latex]
- [latex]x = -x + 2[/latex]
- [latex]\frac{1}{2}x = -x + 2[/latex]
- [latex]5x = 3x + (x + 2)[/latex]
- [latex]\frac{3}{5}x = 1[/latex]
- [latex]\frac{3}{4}x - 2x = 7[/latex]
- [latex]\frac{1}{2}x - x = 7(x + 2)[/latex]
- [latex]\frac{x}{2} + \frac{5}{6} = \frac{x}{3}[/latex]
- [latex]\frac{x}{2} + 2x = \frac{1}{3}[/latex]
- [latex]-3(x - 4) = 12[/latex]
- [latex](3x - 4) - (x - 1) + (2x - 15) = 3x - 7[/latex]
- [latex]3.5x - 5.75x + 1.75x = -1.5[/latex]
- [latex]x - \frac{5x}{2} + 7 = \frac{x}{4}[/latex]
- [latex]\frac{x}{2} + \frac{5}{5} = \frac{2x}{3}[/latex]
- [latex]14 = 5x - (3x - 2)[/latex]
- [latex]\frac{x - 5}{9} = -3[/latex]
- [latex]\frac{x}{4} + 2 = \frac{4}{8}[/latex]
- [latex]-4x = \frac{5(1 - x)}{6}[/latex]
- [latex]\frac{1}{2}x - 3x = 7(x + 5)[/latex]
- [latex]3x + 1 = 2(x - 3) + x[/latex]
Operations with Polynomials
- Perform the indicated operations.
- [latex](3a + 2a^2 + 3a^3) - (a + 2a^2 - 3a^3)[/latex]
- [latex](3a + 2a^2 + \frac{3}{5}a^3) + (6a - \frac{2}{5}a^2 - 3a^3)[/latex]
- [latex](\frac{2}{7}a + 2a^2 + \frac{3}{5}a^3) - (a - \frac{2}{7}a^2 - 3a^3)[/latex]
- [latex](4x - 3)^2[/latex]
- [latex](x - 3)(x^2 + 3x + 9)[/latex]
- [latex](r - 6)(r - 3) - (3r + 2r^2 - 7)[/latex]
Applications with Polynomials
- Answer the following.
- Write the polynomial that represents the perimeter of the triangle.
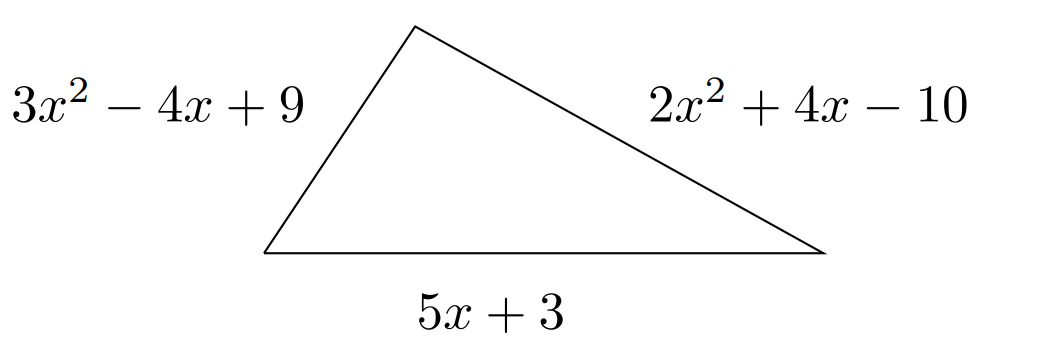
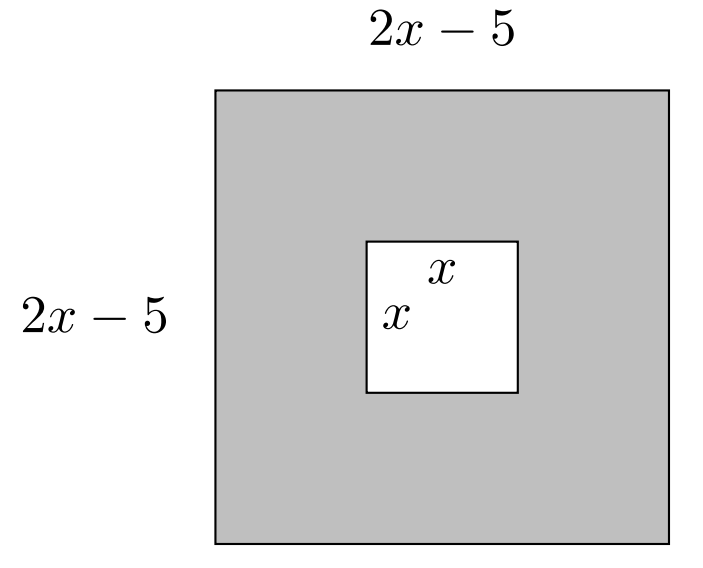
- Find the polynomial that represents the area of the shaded region
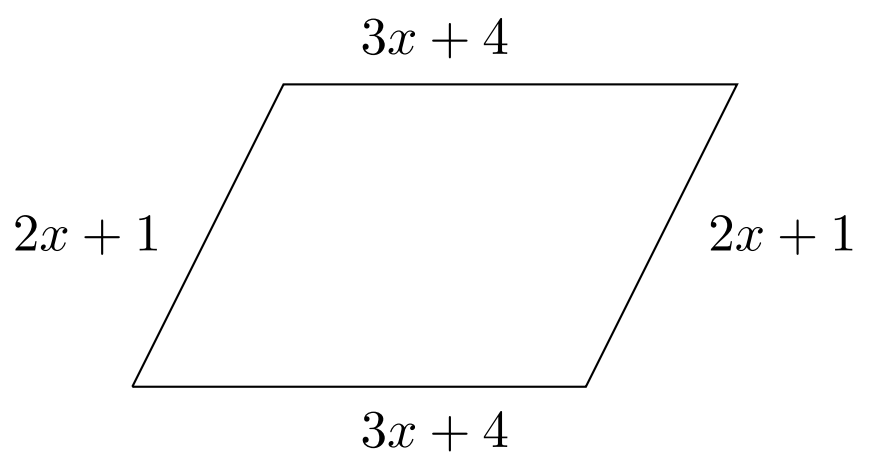
- Write the polynomial that represents the perimeter of the parallelogram in the figure.
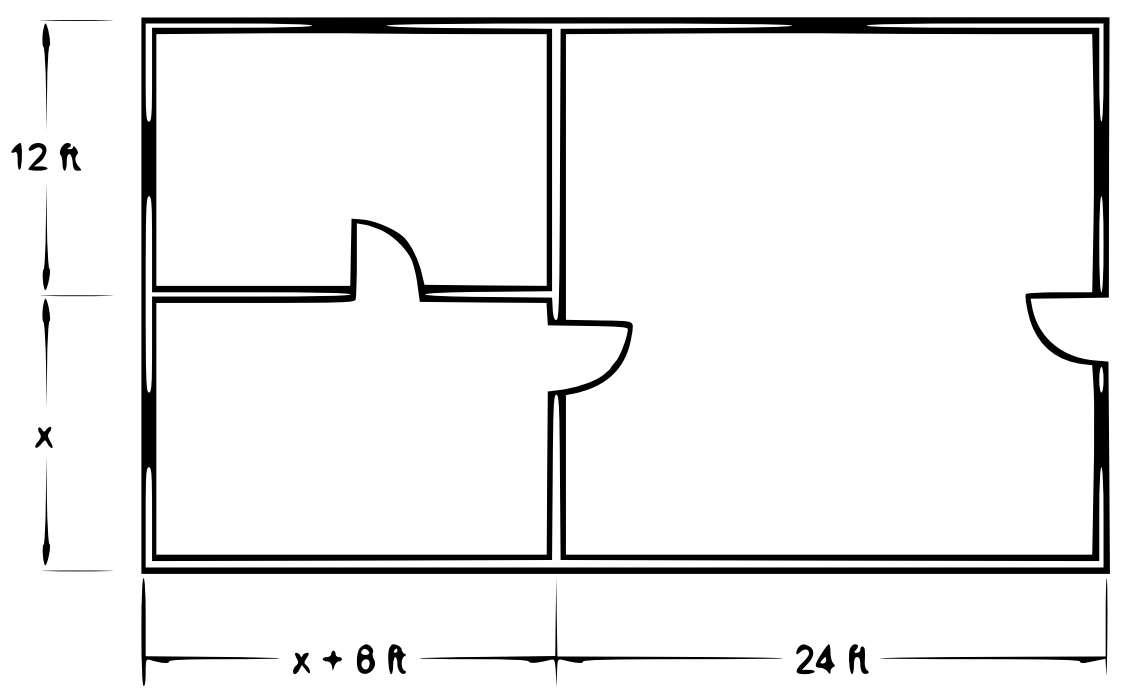
- Write the polynomial that represents the total number of square feet for the floor plan below.
- Write the polynomial that represents the perimeter of the triangle.
Greatest Common Factor
- Factor out the greatest common factor (GCF) from the expressions.
- [latex]6y^2 + 6[/latex]
- [latex]xy^2 - 3y^2[/latex]
- [latex]3x^2 + 6x[/latex]
- [latex]16x^2y^2 - 28xy^2 + 48y^5[/latex]
- [latex]25x^3y^4 - 65x^2y^5 - 80x^4y^3[/latex]
Homework: Operations with Polynomials, Applications, & GCF
- Perform the indicated operations.
- [latex](3x + 2) + (3x - 2)[/latex]
- [latex](3x + 2) - (3x - 2)[/latex]
- [latex](3x + 2)(3x - 2)[/latex]
- [latex]2(3x + 2)[/latex]
- [latex](3x + 2)^2[/latex]
- [latex](3x + 5)(4x - 7)[/latex]
- [latex](3x^2y + 2) + (3xy - 25)[/latex]
- [latex](3x + 4) + (4x - 5)[/latex]
- [latex](x^3 + 7x^2 - x + 9) + (5x^2 + 4x - 5)[/latex]
- [latex](8x + 3) - (x + 4)[/latex]
- [latex](3x + 5)(6x - 7)[/latex]
- [latex](x + 5)(x + 2)[/latex]
- [latex](5x^2 + 8x - 4) - (2x^2 + 6x - 5)[/latex]
- [latex](x + 3)^2[/latex]
- [latex](x^2 - 3x + 7) + (2x^2 + 5x - 6)[/latex]
- [latex](x - 4)(x + 5) - (3x + 2x^2 - 30)[/latex]
- Answer the following.
- Write the polynomial that represents the total volume of the rectangular prism below. Use the formula: [latex]V\;=\;\text{length}\;\cdot\;\text{width}\;\cdot\;\text{height}[/latex]
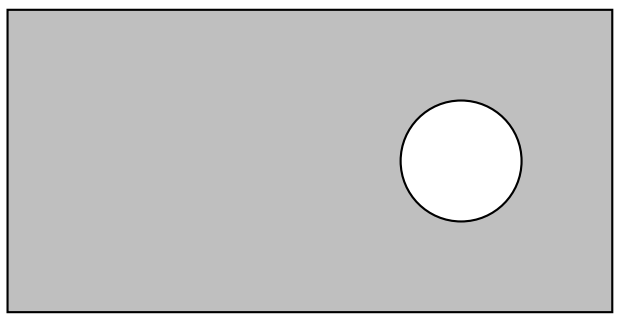
- A countertop pictured below will have a hole drilled to hold a utensil holder. The area of the entire countertop is given by [latex]3x^2+12x+4[/latex]. The area of the hole is given by [latex]x^2+2x+1[/latex]. Write an expression for the area of the countertop that remains after the hole is drilled (the shaded region).
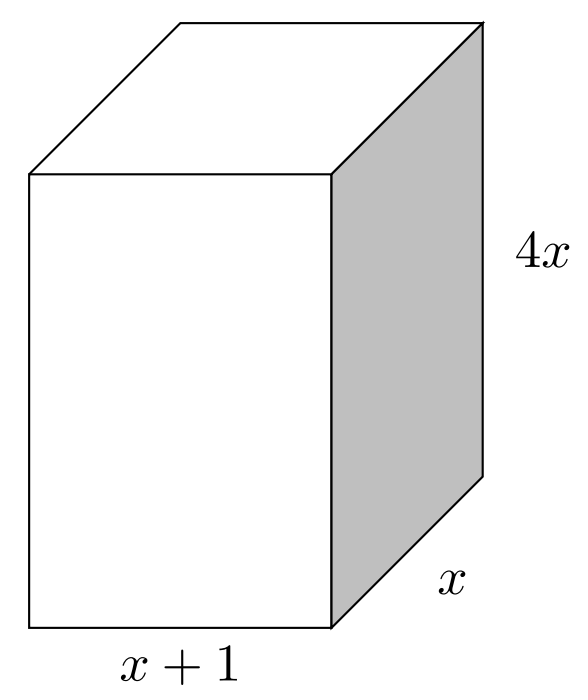
- Write the polynomial that represents the total volume of the rectangular prism below. Use the formula: [latex]V\;=\;\text{length}\;\cdot\;\text{width}\;\cdot\;\text{height}[/latex]
- Factor out the greatest common factor (GCF).
- [latex]6x^2 + 15x[/latex]
- [latex]36x^3 + 90x^5 - 72x^7[/latex]
- [latex]2x^2 - 12x[/latex]
- [latex]14x^2 - 12x + 8[/latex]
- [latex]14x^3 - 12x^2 + 8x[/latex]
- [latex]32x^2 - 16x[/latex]
- [latex]32x^2 - 16x + 8[/latex]

