"

1.4 Linear Graphs – Intercepts Method

1.4.1 Prep

Fill in the blanks.

  1. image
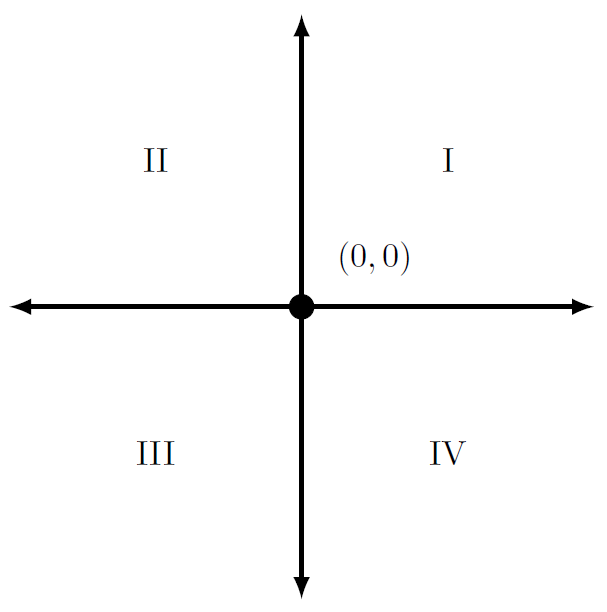
    1. An x-coordinate is positive in quadrant (s) __________ and negative in quadrant(s) _____________.
    2. A y-coordinate is positive in quadrant(s) __________ and negative in quadrant(s) _____________.

Plot the following points.

  1. Plot [latex](2,5),(-2,-5),(7,-3)[/latex], and [latex](-4,6)[/latex]
    image
    1. Plot [latex](0,5),(0,-5)[/latex], [latex](0,-1)[/latex], and [latex](0, 9)[/latex].
      image
    2. These points are called y-intercepts. Discuss what they have in common.
    1. Plot [latex](2,0),(-2,0),(-7,0),[/latex] and [latex](6, 0)[/latex].
      image
    2. These points are called x-intercepts. Discuss what they have in common.

1.4.2 Preview

Linear Equation in Two Variables

A linear equation in two variables is an equation that can be written as

[latex]Ax+By=C[/latex]

where A, B, and C are real numbers.

Try It!

Decide which of the following equations represent a linear equation in two variables.

[latex]3x-5y=10\quad\quad\quad\quad2^x=5[/latex]

[latex]-4x=1\quad\quad\quad\quad\quad\quad2-2x^2+y=1[/latex]

Example

For the linear equation [latex]x+2y=8[/latex], the point (6, 1) is a solution because

[latex]x+2y=8[/latex]

[latex](6)+2(1)=8[/latex]

The x-coordinate is 6, and the y-coordinate is 1.

Try It!

Show that [latex](-2,5)[/latex] is also a solution for [latex]x+2y=8[/latex]

Try It!

Can you find another solution for [latex]x+2y=8?[/latex]
image

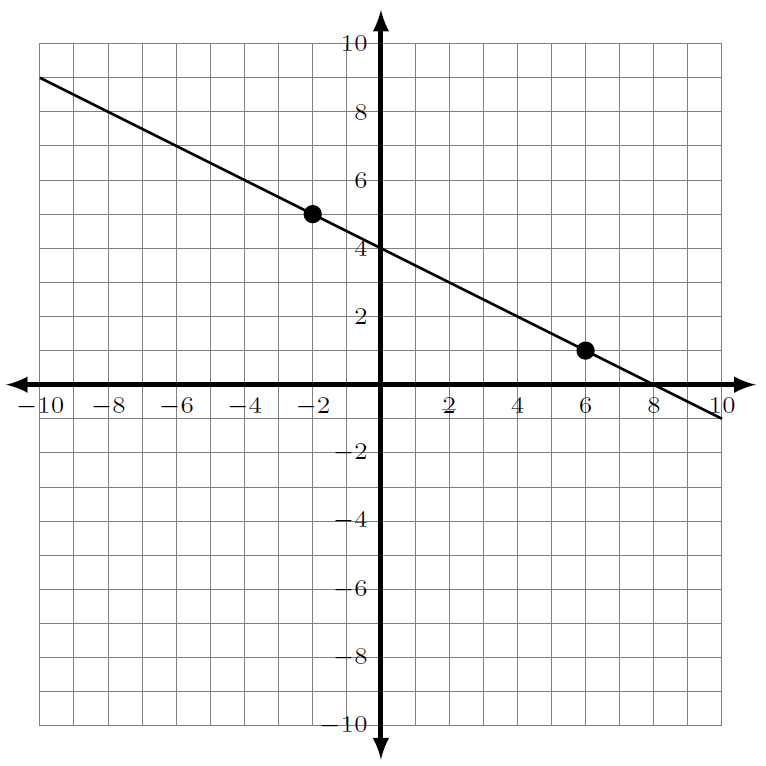
Intercepts

The x-intercept of a line is the point at which its graph crosses the x-axis.

The y-intercept of a line is the point at which its graph crosses the y-axis.

Try It!

Find the x- and y-intercept for each of the following lines.

imageimageimage

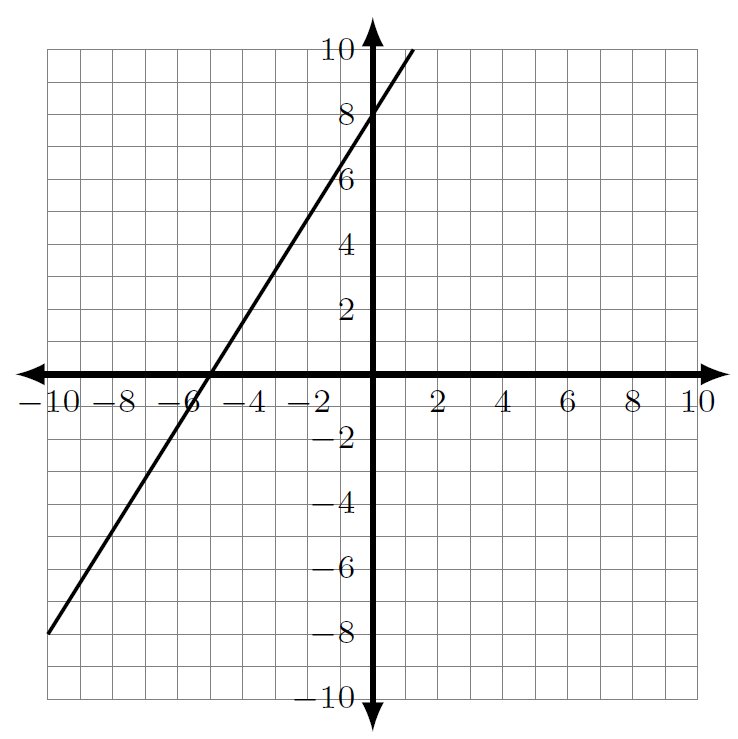
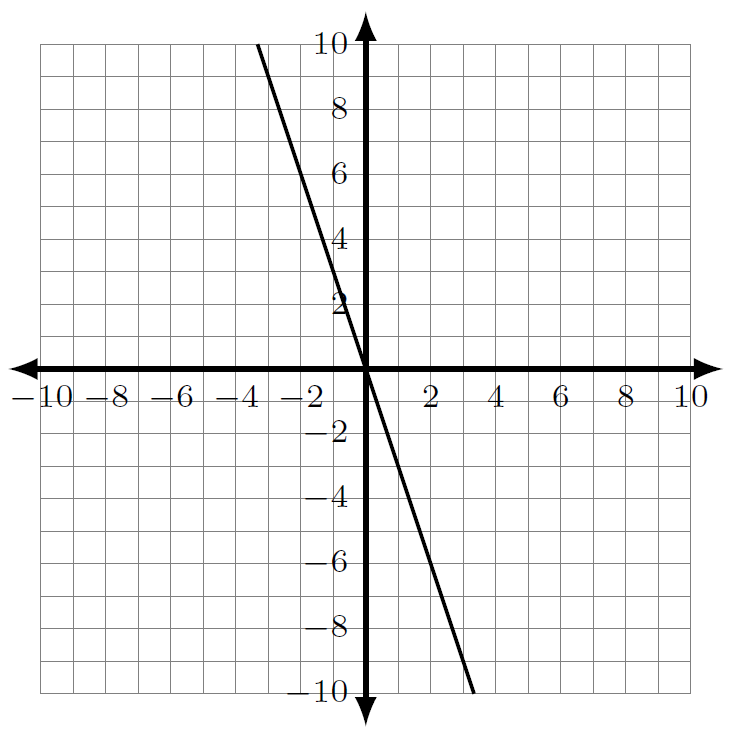
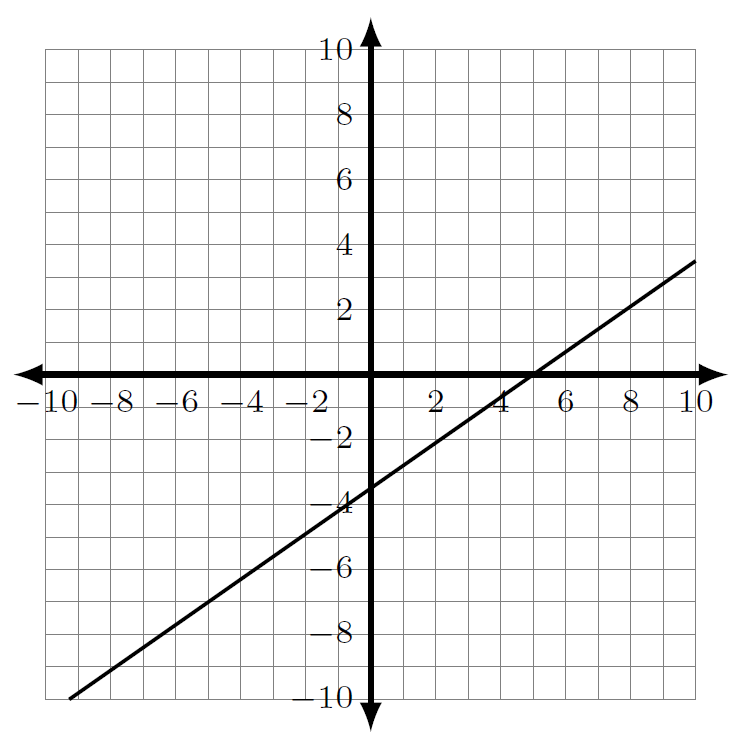
1.4.3 Class Examples

Find the x- and y-intercept for each of the following lines.

  1. [latex]y=-2x+9[/latex]
  2. [latex]y=6+x[/latex]
  3. [latex]12y-2x=6[/latex]
  4. [latex]8x+5y=17[/latex]
  5. Sketch the graph of a line that
    1. does not have an x-intercept.
    2. does not have a y-intercept.
  6. [latex]\frac{5y}2=10[/latex]
  7. [latex]8x=-16[/latex]
  8. Write an equation of a line with y-intercept (0, 5).

Use the Intercepts Method to graph the following lines.

  1. [latex]5x+2y=10[/latex]
    image
  2. [latex]\frac14y-\frac18x=\frac12[/latex]
    image
  3. [latex]2y+\frac14x=-2[/latex]
    image
  4. [latex]12y-2x=6[/latex]
    image
  5. [latex]\frac{5y}2=10[/latex]
    image
  6. [latex]8x=-16[/latex]
    image

1.4.4 Homework

Find three different solutions for the following equations.

  1. [latex]3x-4y=12[/latex]
  2. [latex]-8x-y=16[/latex]

Find the x- and y-intercept for each of the following lines.

  1. [latex]y=8-3x[/latex]
  2. [latex]\frac2{15}x-\frac25y=\frac45[/latex]
  3. [latex]-4x+3y=2[/latex]
  4. [latex]-5y=15[/latex]

Use the Intercepts Method to graph the following lines.

  1. [latex]2x-6y=12[/latex]
    image
  2. [latex]4x-12y=12[/latex]
    image
  3. [latex]\frac12y=-\frac16x+\frac32[/latex]
    image
  4. [latex]2x=8[/latex]
    image

Answer the following.

  1. Write an equation of a line with x-intercept [latex](-2,0)[/latex].
  2. Explain in your own words why you plug in 0 for x to find the y-intercept.
  3. The graph of a line may be represented by more than one equation. For example, the equations [latex]3x-\frac14y=\frac32[/latex] and [latex]y=12x-6[/latex] both define the graph of the same line.
    1. Find the y-intercept for the line with equation [latex]3x-\frac14y=\frac32[/latex]. Show all steps.
    2. Find the y-intercept for the line with equation [latex]y=12x-6[/latex] Show all steps.
    3. For which equation was it easier to find the y-intercept, and why?
  4. Is it possible for a line to have two y-intercepts? Why or why not?
  5. Is it possible to draw a line with two x-intercepts? Why or why not?

License

College Algebra for Non-STEM Majors Copyright © by Amy Collins Montalbano. All Rights Reserved.

Share This Book