"

1.5 Linear Graphs – Slope Intercept Method

1.5.1 Prep

Solve the following equations for y so that each equation is in the form [latex]y=mx+b[/latex].

  1. [latex]2y=3x+8[/latex]
  2. [latex]-3y=3x-9[/latex]
  3. [latex]2x+3y=15[/latex]
  4. [latex]3x-3y=9[/latex]
  5. [latex]-y=2x+1[/latex]
  6. [latex]15y+5x=-15[/latex]
  7. [latex]6x-3y=18[/latex]
  8. [latex]\frac12x=\frac23y=4[/latex]
  9. [latex]\frac12x+2y=6[/latex]
  10. [latex]\frac{x+y}2=-3[/latex]
  11. [latex]\frac13x-2y=\frac23[/latex]
  12. [latex]\frac12x+=\frac34y=3[/latex]

Evaluate [latex]\frac{a-c}{b-d}[/latex] for the given values of a, b, c, and d.

  1. [latex]a=10,\;b=7;\;c=4,\;d=5[/latex]
  2. [latex]a=5,\;b=-7;\;c=-3,\;d=9[/latex]
  3. [latex]a=\frac12,\;b=\frac13;\;c=\frac52,\;d-\frac56[/latex]
  4. [latex]a=-\frac57,\;b=2;\;c=\frac23,\;d=\frac23[/latex]
  5. [latex]a=8,\;b=3;\;c=8,\;d=-2[/latex]
  6. [latex]a=-7,\;b=4;\;c=-1,\;d=4[/latex]
  7. When is having 0 in a fraction defined? When is it undefined? Discuss.

1.5.2 Preview

Slope-Intercept Form

When a linear equation in two variables is written in slope-intercept form

y = mx + b

m is the slope of the line and (0, b) is the y-intercept of the line.

Example

To find the slope and y-intercept of a line, solve for y as shown in the following example.

[latex]3x+5y=10[/latex]

[latex]5y=-3x+10[/latex]

[latex]\frac{5y}5=\frac{-3x}5+\frac{10}5[/latex]

[latex]y=-\frac35x+2[/latex]

The slope is [latex]-\frac35[/latex] and the y-intercept is (0, 2).

Try It!

For the example above, write the reason for each step out to the side.

Try It!

Find the slope and y-intercept for [latex]-4x-3y=21[/latex].

The slope of a line is [latex]m=\frac{{\text{rise}}}{{\text{run}}}=\frac{{\text{change}}\;in\;y}{{\text{change}}\;in\;x}.[/latex]

image

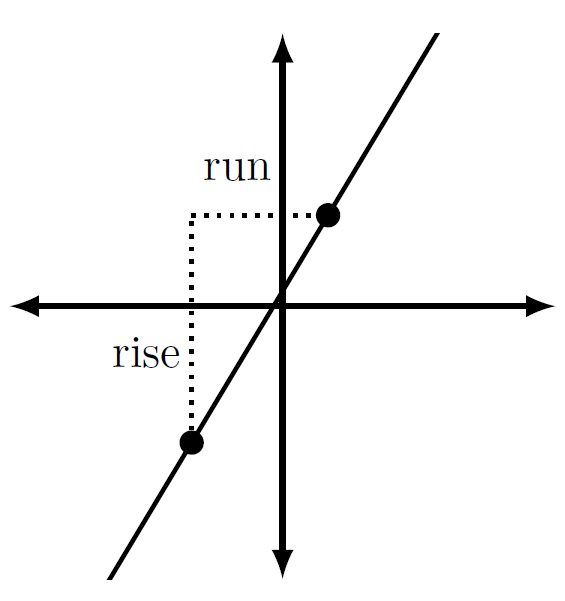
Try It!

Create possible values the rise and run show in the graph above label them on the graph.

Slope Formula

The slope m of the line containing the points (x1, y1) and (x2, y2) is given by

[latex]m=\frac{{\text{rise}}}{{\text{run}}}=\frac{{\text{change in y}}}{{\text{change in x}}}=\frac{y_2-y_1}{x_2-x_1}[/latex]

as long as [latex]x_2\neq x_1[/latex].

Example

The slope of the following line is [latex]m=\frac{{\text{down 3}}}{{\text{right 6}}}=\frac{-3}6=\frac{-1}2=\frac{{\text{down 1}}}{{\text{right 2}}}.[/latex]

imageimage

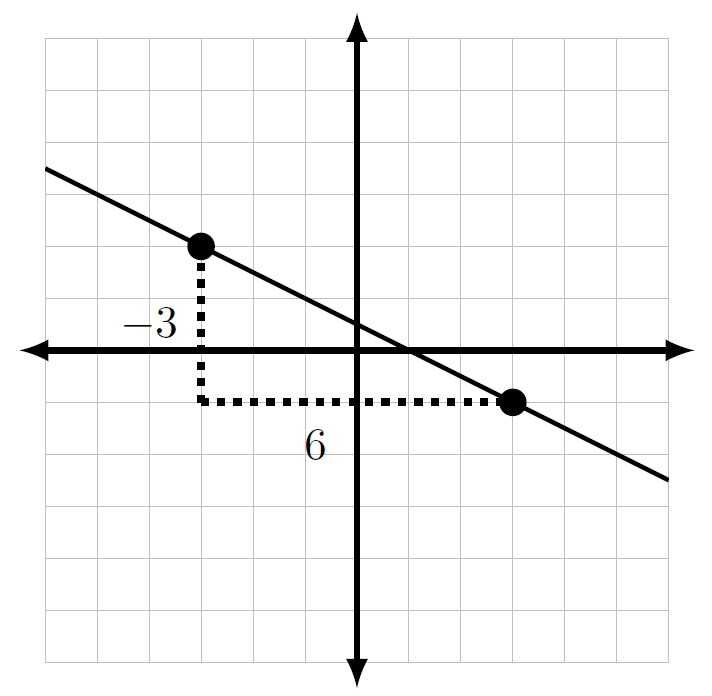
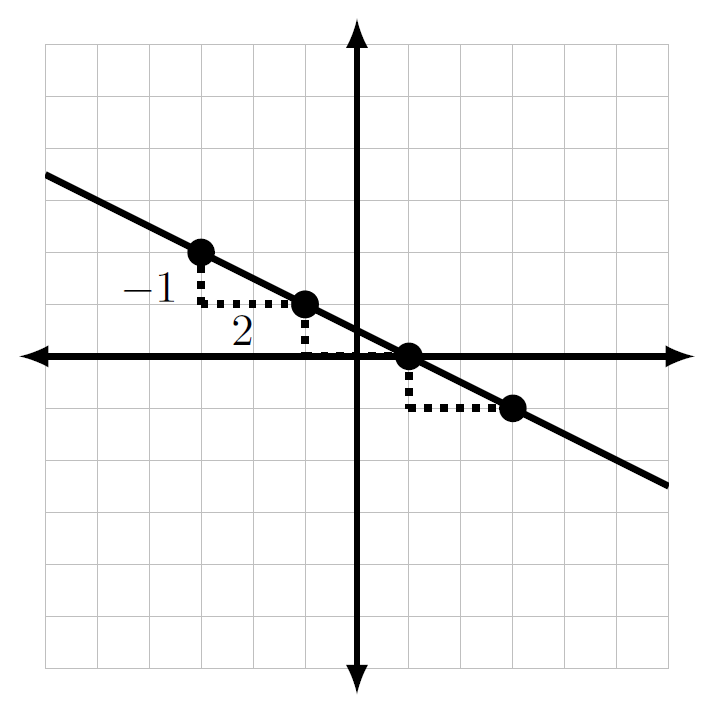
Try It!

  1. Draw two lines that are parallel.
  2. Draw two lines that are perpendicular.

Two nonvertical lines are parallel if they have the same slope but different y-intercepts.

Two nonvertical lines are perpendicular if the slope of one is the negative reciprocal of the slope of the other.

1.5.3 Class Examples

Write the Slope-Intercept Form and identify the slope and y-intercept for each line below.

  1. [latex]\frac25x+\frac56y=10[/latex]
  2. [latex]x-3y=9[/latex]
  3. [latex]2x+2y=8[/latex]
  4. [latex]\frac14x-y=\frac23[/latex]
  5. [latex]\frac12x-\frac23y=5[/latex]
  6. [latex]\frac23y=-2[/latex]

Answer the following.

  1. Sketch the graphs of three different lines whose slopes are positive, negative, and zero.
  2. Is it possible for a line to have two different slopes? Why or why not?

Use the Slope-Intercept Method to graph the following lines.

  1. [latex]y=-\frac32x-5[/latex]
    image
  2. [latex]3y=-x+9[/latex]
    image
  3. [latex]-4y+x=12[/latex]
    image
  4. [latex]\frac14y-\frac12x=\frac34[/latex]
    image
  5. [latex]-6y=12[/latex]
    image
  6. [latex]\frac12x-\frac23y=\frac52[/latex]
    image

Find the slope of the line through the indicated points.

  1. Find the slope of the line through the points [latex](-1,4)[/latex] and [latex](5, 2)[/latex]
    1. using the slope formula.
    2. using the graph.
  2. [latex](4,3)[/latex] and [latex]\left(\frac72,\frac52\right)[/latex]
  3. [latex](-2,3)[/latex] and [latex](7,-8)[/latex]
  4. [latex](5,-3)[/latex] and [latex]\left(-2,\frac35\right)[/latex]
  5. [latex]\left(\frac56,-\frac35\right)[/latex] and [latex]\left(-2,\frac34\right)[/latex]

Solve the following.

  1. Which of the following pairs of lines are parallel or perpendicular?
    1. [latex]y=-\frac16x+11[/latex]
    2. [latex]y=6x-\frac12[/latex]
    3. [latex]x+6y=30[/latex]
    4. [latex]2x-12y=15[/latex]

1.5.4 Homework

Write the Slope-Intercept Form and identify the slope and y-intercept for each line below.

  1. [latex]2y=3x+8[/latex]
  2. [latex]-3y=3x-9[/latex]
  3. [latex]2x+3y=15[/latex]
  4. [latex]6x-3y=9[/latex]
  5. [latex]-3y=12[/latex]
  6. [latex]\frac12x=8[/latex]
  7. [latex]\frac13x-2y=\frac23[/latex]
  8. [latex]\frac12x-\frac23y=4[/latex]
  9. Write an equation for a line with slope [latex]\frac34[/latex]
  10. Write an equation for a line with y-intercept [latex](0,-50)[/latex]

Use the Slope-Intercept Method to graph the following lines.

  1. [latex]2x+3y=15[/latex]
    image
  2. [latex]-5x+y=1[/latex]
    image
  3. [latex]\frac58x-\frac14y=\frac12[/latex]
    image
  4. [latex]\frac14x+\frac12y=-\frac23[/latex]
    image
  5. Write this line in Slope-Intercept Form:[latex]-4x+y=0[/latex] Find both the x- and y-intercepts. What can you do to find another point on the graph of the line?
    image
    1. Plot the points [latex](6,-2){\text{and}}(8,-3)[/latex], then draw the line that passes through them.
    2. Find the slope of this line by counting the rise over run between these two points.
      image

Find the slope of the line through the two points.

  1. [latex](6,-2)[/latex] and [latex](8,−3)[/latex]
  2. [latex]\left(\frac23,\frac56\right)[/latex] and [latex]\left(\frac53,-\frac76\right)[/latex]
  3. [latex](5,−3)[/latex] and [latex]\left(-2,-\frac38\right)[/latex]
  4. [latex]\left(1,\frac45\right)[/latex] and [latex]\left(\frac12,-\frac47\right)[/latex]
  5. [latex](5,−3)[/latex] and [latex](1,−3)[/latex]
  6. [latex](1, 4)[/latex] and [latex](1,−7)[/latex]

Parallel and Perpendicular Lines

  1. Use the following equations to answer the following.
    Line 1: [latex]y=-\frac25x+5[/latex]
    Line 2: [latex]2x+5y=15[/latex]
    1. Find the slope of Line 1.
    2. Find the slope of Line 2.
    3. What do you notice about their slopes, and what does it mean about their graphs?
  2. Use the following equations to answer the following.
    Line A: [latex]x-3y=1[/latex]
    Line B: [latex]y-3x+4=1-6x[/latex]
    1. Find the slope of Line A.
    2. Find the slope of Line B.
    3. What do you notice about their slopes, and what does it mean about their graphs?

License

College Algebra for Non-STEM Majors Copyright © by Amy Collins Montalbano. All Rights Reserved.

Share This Book