"

2.2 Applications of Quadratic Functions

2.2.1 Prep

Answer the following.

  1. An object is launched directly upward at 19.6 meters per second from a 58.8-meter tall platform. The function for the object’s distance from the ground D at time t seconds after launch is [latex]D\left(t\right)=-4.9t^2+19.6t+58.8[/latex], where D is in meters. When does the object strike the ground?
    1. The speed of the object is measured in which units?
    2. How tall is the platform?
    3. Write the function that models this problem.
    4. What does D represent? D is measured in which units?
    5. What is the question being asked?
  2. A ball is thrown into the air. The height of the ball above the ground is represented by the function [latex]h\left(t\right)=-16t^2+8t[/latex], where h is in feet and t is in seconds.
    1. The speed of the object is measured in which units?
    2. What does the variable h represent in this problem?
    3. h is measured in which unit?
    4. What does the variable t represent in this problem?
    5. t is measured in which unit?
    6. Sketch the path of the ball. Let the x-axis measure time and the y-axis measure height. Is the graph a line or a parabola?

Answer the following.

  1. An object is launched directly upward at 19.6 meters per second from a 58.8-meter tall platform. The function for the object’s distance from the ground D at time t seconds after launch is [latex]D\left(t\right)=-4.9t^2+19.6t+58.8[/latex], where D is in meters.
    1. Which unit should be used to answer “When does the object strike the ground?”
    2. Which unit should be used to answer “What is the maximum height?”
    3. Which unit should be used to answer “How long does it take the object to hit the ground?”
  2. A ball is thrown into the air. The height of the ball above the ground is represented by the function [latex]h\left(t\right)=-16t^2+8t[/latex], where h is in feet and t is in seconds.
    1. Which unit should be used to answer “What is the maximum height?”
    2. Which unit should be used to answer “When does it reach maximum height?”
  3. What if you forget to include units with an answer? Discuss this scenario. You read a recipe that calls for [latex]\frac14[/latex] of peanut butter. How much peanut butter do you use?

Which word is more appropriate for each of the following scenarios: approximate or exact?

  1. Paying your CPS bill
  2. Telling someone how many students attend NVC
  3. Writing [latex]\frac14[/latex] as 0.25
  4. Writing [latex]\frac13[/latex] as 0.3
  5. Giving the correct amount of medicine to a patient
  6. Estimating your grocery bill as you stand in line at the checkout

Use either equal to [latex]\left(=\right)[/latex] or approximately [latex]\left(\approx\right)[/latex] to fill in the blanks.

  1. [latex]0.5\;\_\_\_\_\_\_\_\_\_\_\frac12[/latex]
  2. [latex]\frac17\;\_\_\_\_\_\_\_\_\_\_\;0.143[/latex]
  3. [latex]\frac13\;\_\_\_\_\_\_\_\_\_\_\;33\%[/latex]
  4. [latex]\frac7{11}\;\_\_\_\_\_\_\_\_\_\_\;0.\overline{63}[/latex]
  5. [latex]10\%\;\_\_\_\_\_\_\_\_\_\_\;0.0993[/latex]
  6. [latex]\frac23\;\_\_\_\_\_\_\_\_\_\_\;0.67[/latex]
  7. [latex]\frac56\;\_\_\_\_\_\_\_\_\_\_\;83\%[/latex]
  8. [latex]12\%\;\_\_\_\_\_\_\_\_\_\_\;\frac3{25}[/latex]
  9. [latex]4.08\%\;\_\_\_\_\_\_\_\_\_\_\;0.04[/latex]

Round to the indicated place value.

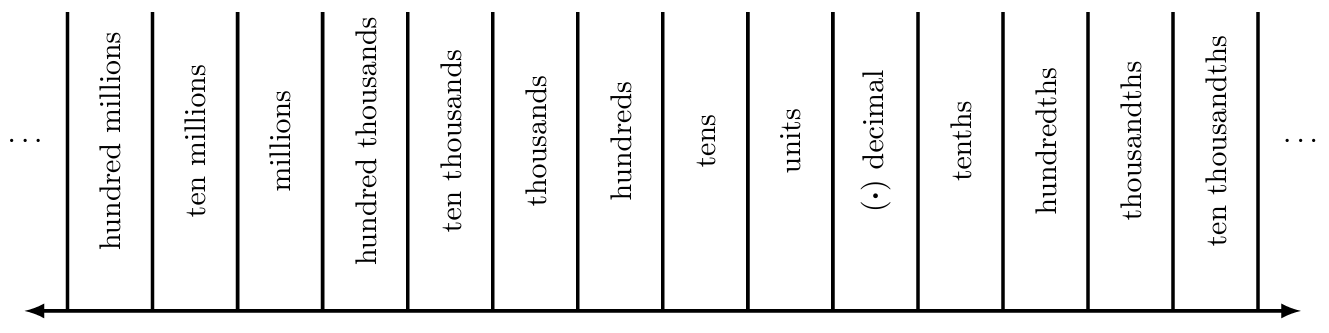
  1. Round to the nearest hundred: [latex]3,587[/latex]
  2. Round to the nearest unit: [latex]45.27[/latex]
  3. Round to the nearest hundredth: [latex]39.823[/latex]
  4. Round to two decimal places: [latex]72.485[/latex]
  5. Round to three decimal places: [latex]-3.0938[/latex]
  6. Round to the nearest tenth: [latex]\frac27[/latex]
  7. Round to two decimal places: [latex]0.2987[/latex]
  8. Round to two decimal places: [latex]\frac{149}{251}[/latex]

2.2.2 Preview

Try It!

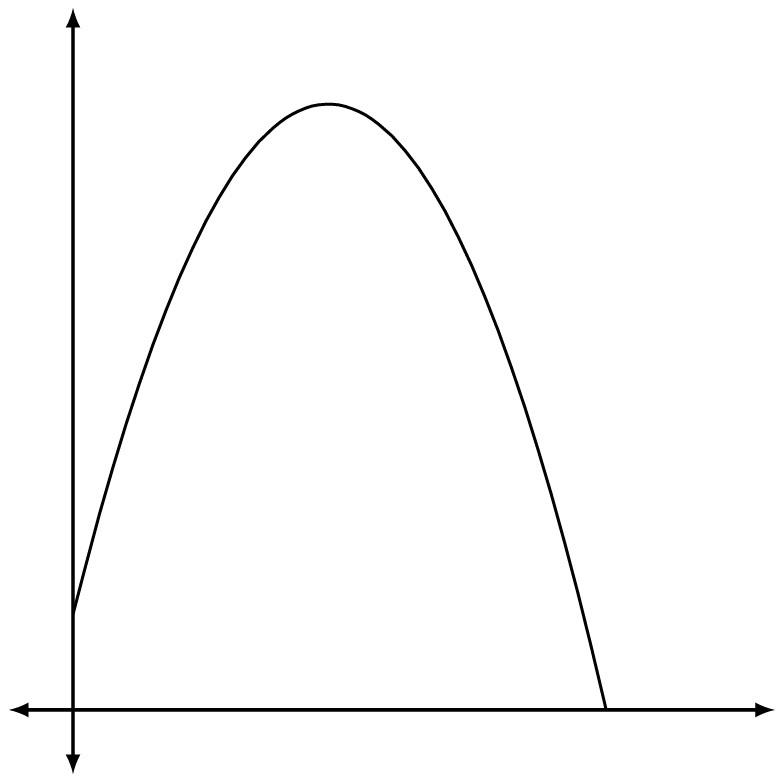
Our goal in the next section is to solve word problems involving quadratic functions. Suppose the graph below represents the path of a ball that has been thrown into the air. Label the following on the graph below.

  1. Draw a over the point on the graph that represents where the ball hit the ground.
  2. Draw a over the point on the graph where the ball reached its highest point.
  3. Draw a over the point on the graph where the ball was first thrown.

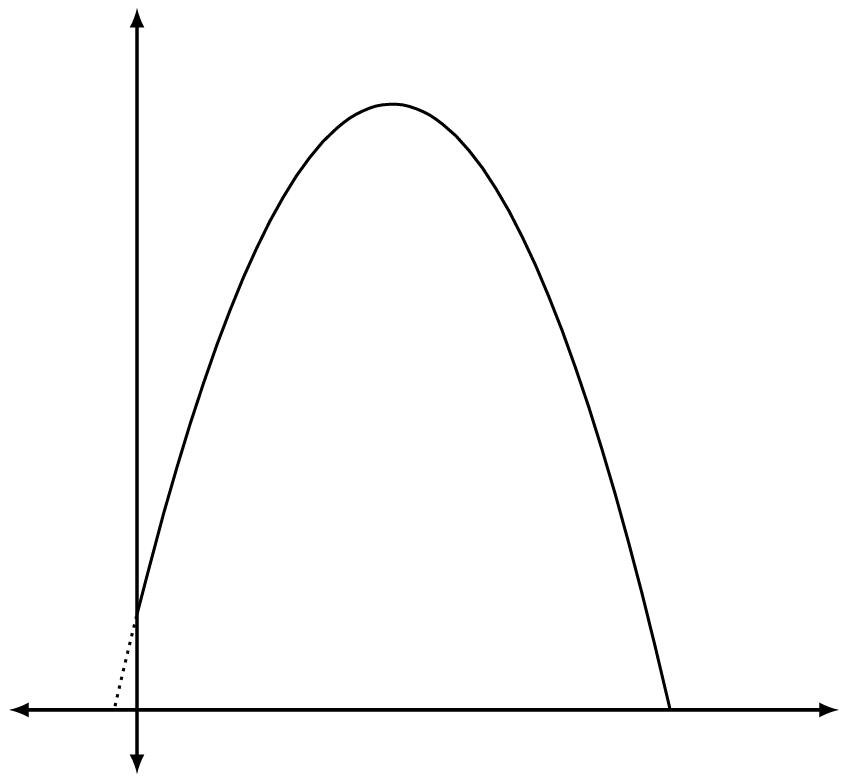
Try It!

Suppose the graph below represents the path of a toy rocket that has been launched into the air. If the x-axis measures the time since the rocket was launched, and the y-axis measures the height of the rocket, answer the following.

  1. Why does the graph only show the portion of the parabola in Quadrant I?
  2. Why do we ignore one of the x-intercepts for this graph?

2.2.3 Classwork

Application of Quadratic Functions

To solve the word problems involving quadratic functions on the following pages, look for key words or phrases that relate to some part of the graph. Consider a quadratic function that represents an object being thrown.

Label the y-intercept on the graph.

  1. Words that mean y-intercept:
  2. Method to find y-intercept:
  3. Function notation for y-intercept:

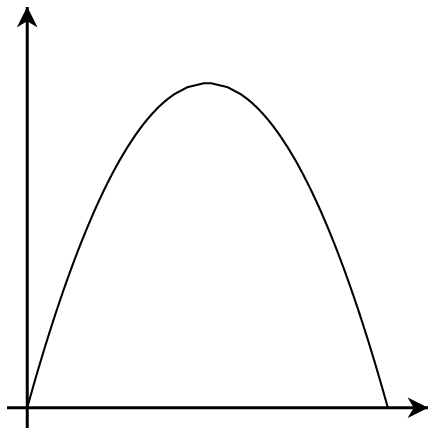
Label the x-intercepts on the graph.

  1. Words that mean x-intercept:
  2. Method to find x-intercept:
  3. Function notation for x-intercept:

Label the vertex on the graph.(A vertex has two coordinates, x and y.)

  1. Words that mean the x-coordinate of the vertex:
  2. Words that mean the y-coordinate of the vertex:
  3. Method to find the vertex:
  4. Function notation for vertex:

Answer the following questions

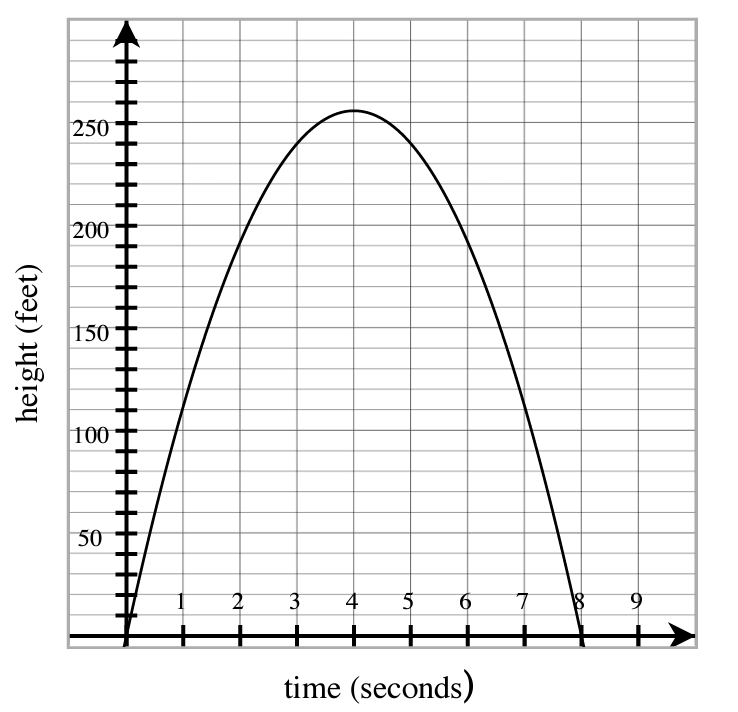
  1. The graph models the height h (in feet) of a small rocket t seconds after it is launched. The path of the rocket is given by the function [latex]h\left(t\right)=-16t^2+128t.[/latex]
    1. How long is the rocket in the air?
    2. What is the maximum height of the rocket?
      1. What is the height of the rocket 2 seconds after it is launched?
      2. Is the rocket going up or down 2 seconds after it is launched?
      1. What is the height of the rocket 6 seconds after it is launched?
      2. Is the rocket going up or down 6 seconds after it is launched?
    5. When is the rocket 112 feet high? Estimate.
    6. Do you think the rocket is traveling faster from 0 to 1 second, or from 3 to 4 seconds? Explain your answer.
    7. Write a reasonable domain and range for this event.
  2. Use the graphs to answer the following.
    1. Estimate the y-intercept of both graphs.
    2. Interpret and compare the vertex of the graph on the left to the vertex of the graph on the right.
    3. Interpret and compare the x-intercepts of both graphs.
    4. Which of your previous answers tells you about domain? About range?
  3. After t seconds, a ball is tossed in the air. The ball reaches a height of h feet given by the function [latex]h\left(t\right)=23+144t-16t^2[/latex].
    1. Fill in the table for the missing values.
      [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol t}[/latex] [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol y}[/latex]
      [latex]0[/latex]
      [latex]3[/latex]
      [latex]6[/latex]
      [latex]9[/latex]
      [latex]10[/latex]
    2. From what height was the ball thrown?
    3. What is the height of the ball at 3 seconds?
    4. Does the table of values show you the maximum height? What is the maximum height the ball will reach?
    5. Use the table of values to estimate how many seconds it will take for the ball to hit the ground.
  4. A ball is thrown in the air. The height of the ball above the ground is represented by the function [latex]h\left(t\right)=-4.9t^2+2.45t+2[/latex], where h is in meters and t is in seconds.
    1. From what height is the ball thrown?
    2. What is the maximum height of the ball?
    3. How long is the ball at or above 3 meters?
  5. A half-pipe ramp at a skate park is approximately in the shape of a parabola. If x stands for the horizontal distance (in feet) from where a skateboarder starts a ride on the half-pipe, and y stands for the height (in feet) of a skateboarder from the ground, then the position of a skateboarder on the ramp is given by [latex]y=0.42x^2-5.67x+20[/latex]. Find and interpret the vertex.
  6. In science class, students were asked to create a container to hold an egg which they would then drop from a window. The function [latex]h\left(t\right)=-16t^2+25[/latex] gives the container’s height h (in feet) after t seconds.
    1. How high is the window?
    2. Find the maximum height of the container. How long does it take to reach its maximum height? Relate this result to your answer from part (a).
  7. Eddie is jumping on a trampoline. His height h (in feet) at time t (in seconds) can be modeled by the function [latex]h\left(t\right)=-16t^2+20t+6.[/latex]
    1. Will Eddie reach a height of 14 feet?
    2. How tall is the trampoline?

2.2.4 Homework

Answer the following.

  1. A rocket carrying fireworks is launched from a hill above a lake. The rocket will fall into the lake after exploding at its maximum height. The rocket’s height above the surface of the lake is given by [latex]h\left(t\right)=-16t^2+60t+80.[/latex], where h is in feet and t is in seconds.
    1. Fill in the table for the missing values.
      [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol t}[/latex] [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol y}[/latex]
      [latex]0[/latex]
      [latex]1[/latex]
      [latex]2[/latex]
      [latex]3[/latex]
      [latex]4[/latex]
      [latex]5[/latex]
    2. From what height was the rocket launched?
    3. What is the height of the rocket at 1.5 seconds?
    4. Does the table of values show you the maximum height? What is the maximum height the rocket will reach?
    5. Use the table of values to estimate how many seconds it will take for the rocket to hit the surface of the lake.
  2. At t seconds, the height h, in feet, of a baseball pitched into the air is given by the function below

    [latex]h\left(t\right)=-16t^2+20t+8.[/latex]

    1. What is its height before the pitch?
    2. How long does it take for the ball to reach its highest point?
    3. What is its highest point?
  3. The graphs below represent the paths of two different football punts.
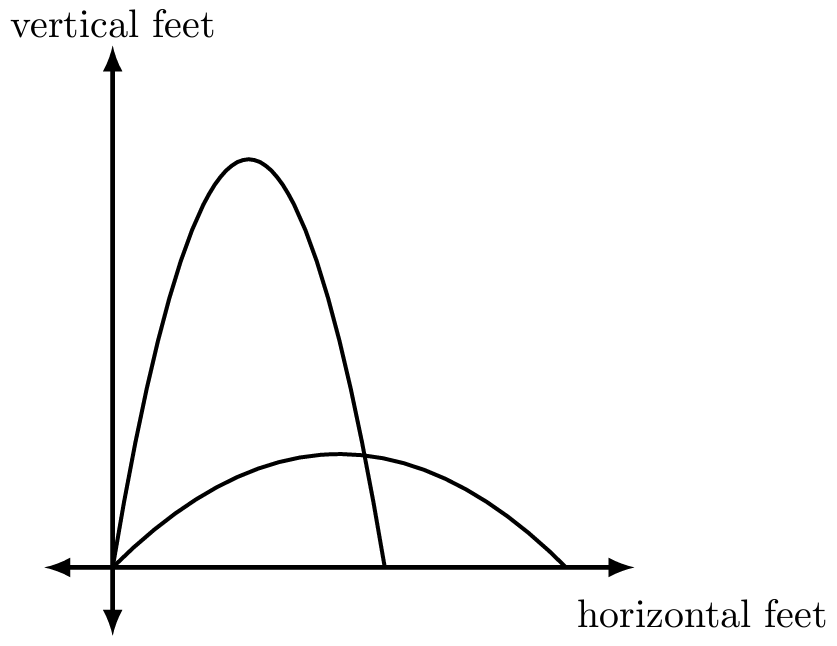
    1. Estimate the y-intercept of both graphs.
    2. Interpret and compare the vertex of the graph on the left to the vertex of the graph on the right.
    3. Interpret and compare the x-intercepts of both graphs.
    4. Which of your previous answers tells you about domain? About range?
    5. Which punt do you think is better and why?
  4. When Greg dives from a platform with an initial upward velocity of 12 ft/s, his height h (in feet) above the water is modeled by the function: [latex]h\left(t\right)=-16t^2+12t+33[/latex], where t represents the number of seconds after the jump.
    1. How high is the platform?
    2. When does Greg reach his maximum height?
    3. What is Greg’s maximum height?
  5. The number of parking spaces, P, available at Northwest Vista’s campus t hours after 7 A.M. each morning can be modeled by [latex]P\left(t\right)=500t^2-3000t+4540.[/latex]
    1. Find and interpret the y-intercept.
    2. Find and interpret the vertex.
  6. The Apollo’s Chariot is a rollercoaster at Busch Gardens with a top speed of 117 km/hr. Its initial (and tallest) descent can be modeled by [latex]h\left(t\right)=52-4.9t^2[/latex], where h is in meters and t is in seconds. What is the maximum height reached by this ride? When does this occur?

License

College Algebra for Non-STEM Majors Copyright © by Amy Collins Montalbano. All Rights Reserved.

Share This Book