"

2.3 Solving Using Quadratic Formula

2.3.1 Prep

Consider the expression:[latex]\sqrt{b^2-4ac}[/latex]

There are multiple operations at work here. What operations do you see?

When we substitute values for a, b, and c, we must correctly apply the order of operations.

Example

Evaluate [latex]\sqrt{b^2-4ac}\;\mathrm{for}\;a=2,b=7,\;\mathrm{and}\;c=3.[/latex]

[latex]\sqrt{\left(7\right)^2-4\left(2\right)\left(3\right)}[/latex]

The square root is a grouping symbol, so we evaluate the entire expression underneath the root symbol first.

We must evaluate the expression using correct order of operations.

Try It!

Evaluate the expression step by step and identify the operation being used in that step in the blank below that step.

[latex]\sqrt{\left(7\right)^2\;4\left(2\right)\left(3\right)}=\sqrt{\;\;\;\;\;\;\;\;\;\;\;\;\;\;}=\sqrt{\;\;\;\;\;\;\;\;\;\;\;\;\;\;}=\sqrt{\;\;\;\;\;\;\;\;\;\;\;\;\;\;}=[/latex]

Operation: __________________ _________________ _________________

Evaluate [latex]\sqrt{b^2-4ac}[/latex] for the given values of a, b, and c.

  1. [latex]a=12,\;b=11,\;c=2[/latex]
  2. [latex]a=1,\;b=-4,\;c=-21[/latex]
  3. [latex]a=15,\;b=13,\;c=-12[/latex]
  4. What do you need to be careful about if b is negative? What if c is negative?

Simplify.

  1. [latex]\sqrt{12}[/latex]
  2. [latex]\sqrt{72}[/latex]
  3. [latex]\frac{10\pm\sqrt{16}}4[/latex]
  4. [latex]\frac{-6\pm\sqrt{64}}{-2}[/latex]
  5. [latex]\frac{2\pm\sqrt{20}}2[/latex]
  6. [latex]\frac{15\pm\sqrt{45}}6[/latex]

Simplify the following using the imaginary number [latex]i=\sqrt{-1}[/latex]

  1. [latex]\sqrt{-36}[/latex]
  2. [latex]\sqrt{-72}[/latex]
  3. [latex]\sqrt{-\frac4{25}}[/latex]
  4. [latex]\frac{-12\pm\sqrt{-36}}4[/latex]
  5. [latex]\frac{5\pm\sqrt{-18}}2[/latex]
  6. [latex]\frac{-8\pm\sqrt{-144}}{-4}[/latex]

2.3.2 Preview

A quadratic equation in standard form is modeled by

[latex]ax^2+bx+c=0[/latex]

where x is a variable and the coefficients a, b, and c are real numbers, but [latex]a\neq0.[/latex].

Example

The following equation is a quadratic equation in standard form.

[latex]2x^2-7x+10=0[/latex]

Notice that the equation is arranged from highest to lowest power of the variable x and equals to 0. The coefficients are

[latex]a=2,\;b=-7,c=10[/latex]

Example

The following equation is a quadratic equation, but it is not in standard form since it is not equal to 0.

[latex]x^2+2x+5=10-3x[/latex]

To rearrange the equation to standard form, we may use the addition property of equality.

[latex]\begin{array}{l}x^2+2x+5=10-3x\\[0.5em]x^2+2x+5+3x=10-\cancel{3x}+\cancel{3x}\\[0.5em]x^2+5x+5=10\\[0.5em]x^2+5x+5-10=\cancel{10}-\cancel{10}\\[0.5em]x^2+5x-5=0\end{array}[/latex]

Therefore, [latex]a=1, b=5[/latex] and [latex]c=-5[/latex].

Try It!

Rearrange the following quadratic equation to standard form. Then find the coefficients a,b, and c.

[latex]405=10+116x-16x^2[/latex]

Example

The graph of [latex]f(x)=2x^2+5x-3[/latex] is given.

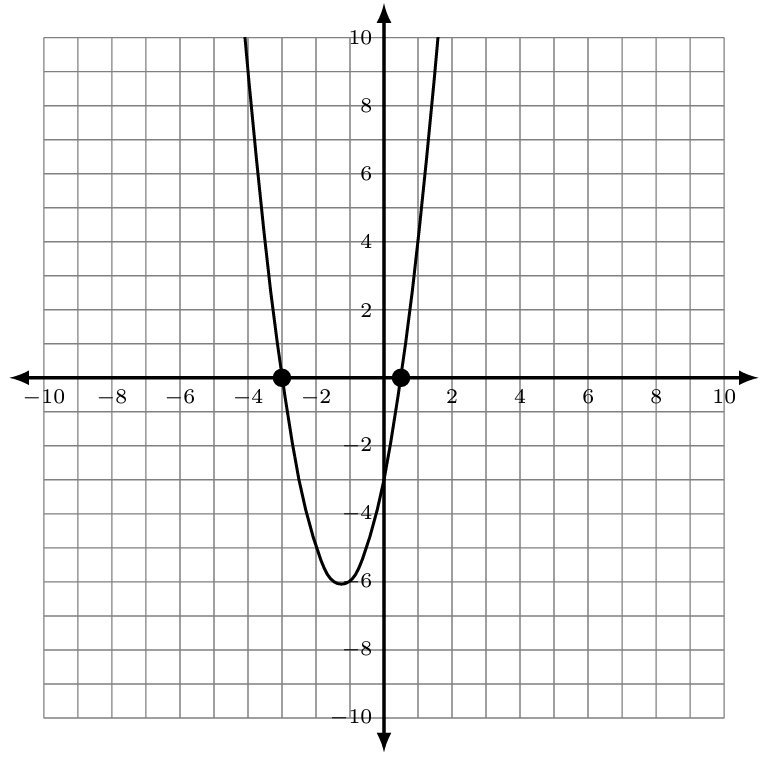
The x-intercepts for the graph are [latex]\left(-3,0\right)[/latex] and [latex]\left(\frac12,0\right)[/latex]. Recall that x-intercepts are found by setting the function equal to 0. This means the solutions for the resulting quadratic equation [latex]2x^2+5x-3=0[/latex] are [latex]x=-3[/latex] and [latex]x=\frac12[/latex].

Try It!

Verify that [latex]x=-3[/latex] and [latex]x=\frac12[/latex] are solutions for the equation above. For [latex]f\left(x\right)=2x^2+5x-3[/latex], find

  1. [latex]f\left(-3\right)[/latex]
  2. [latex]f\left(\frac12\right)[/latex]

2.3.3 Classwork

To find x-intercept(s) for the graphs of quadratic functions, we must solve [latex]ax^2+bx+c=0.[/latex]

The Quadratic Formula:

If [latex]ax^2+bx+c=0[/latex], where [latex]a\neq0[/latex], then

[latex]x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}[/latex]

Writing the Quadratic Formula using two fractions is helpful for two reasons: (1) it helps prevent incorrect canceling, and (2) it makes a connection to the corresponding graph.

[latex]x=\frac{-(b)}{2a}\pm\frac{\sqrt{(b)^2-4ac}}{2a}[/latex]

Use four separate steps to help prevent errors.

Identify the coefficients. Find the axis of symmetry value. Evaluate the discriminant. Simplify the radical. Combine previous values, and simplify.
[latex]a=[/latex]

[latex]b=[/latex]

[latex]c=[/latex]

 [latex]\frac{-\left(b\right)}{2a}[/latex] [latex]\left(b\right)^2-4ac[/latex] [latex]\sqrt{\left(b\right)^2-4ac}[/latex] [latex]x=\frac{-(b)}{2a}\pm\frac{\sqrt{(b)^2-4ac}}{2a}[/latex]

Solve using the Quadratic Formula.

  1. [latex]x^2-4x-3=0[/latex]
  2. [latex]x^2+12=9[/latex]
  3. [latex]x^2=-5x+2[/latex]
  4. [latex]x^2-3x+6=1[/latex]
  5. [latex]x^2+4x+17=8-2x[/latex]
  6. [latex]x^2-\frac32x-\frac14=0[/latex]
  7. [latex]5x^2-3x-1=0[/latex]
  8. [latex]-x^2+7x-18=0[/latex]
  9. [latex]0.16t^2+1=0[/latex]
  10. [latex]3x^2-11x-4=x^2-4x[/latex]
  11. [latex]\frac{2x^2}5-\frac14=\frac{-x}5[/latex]
  12. [latex]0.25x^2-1.125x=0[/latex]

Before doing work to find the 𝑥 -intercept(s), we may evaluate the discriminant to determine the number of 𝑥 -intercepts.

Discriminant How many roots and what type? What can you say about the graph?
[latex]b^2-4ac[/latex] < 0
[latex]b^2-4ac=0[/latex]
[latex]b^2-4ac>0[/latex]

Use the discriminant to determine the number of 𝑥 -intercepts. Do not graph.

  1. [latex]f(x)=2x^2-4x-3[/latex]
  2. [latex]f(x)=4x^2-12x+9[/latex]
  3. [latex]f(x)=-3x^2+5x-8[/latex]
  4. Spot the error and correct it.

[latex]x=\frac{2\pm\sqrt{121}}4[/latex]

A Student’s Answer:[latex]\frac{2\pm\sqrt{11}}4[/latex]

  1. Spot the error and correct it.

[latex]4x^2=12x[/latex]

[latex]a=1\quad b=0\quad c=-12[/latex]

Sketch the graph and identify the following characteristics for the function.

  1. [latex]f(x)=-2x^2+4x+1[/latex]

    Opens: Up / Down

    Axis of Symmetry:

    Vertex:

    y-intercept:

    x-intercept(s):

    Domain:

    Range:

Answer the following.

  1. After t seconds, a ball is tossed in the air. The ball reaches a height of h feet given by the function [latex]h\left(t\right)=5+144t-16t^2[/latex].
    1. What is the height of the ball at 3 seconds?
    2. What is the maximum height the ball will reach?
    3. Find the number of seconds the ball is in the air when it reaches a height of 229 feet.
    4. How many seconds will it take the ball to hit the ground? Round to two decimal places.
    5. Write a reasonable domain and range for this situation. Round to two decimal places.
  2. A ball is thrown upward from a height of 15 meters, with an initial upward velocity of 5 m/s. Use the function [latex]h(t)=-4.9t^2+5t+15[/latex] where h is in meters and t is in seconds to find how long it will take the ball to hit the ground. Graph this function below.

2.3.4 Homework

Simplify.

  1. [latex]\sqrt{175}[/latex]
  2. [latex]\frac{18\pm\sqrt{27}}6[/latex]
  3. [latex]\sqrt{-300}[/latex]
  4. [latex]\frac{20\pm\sqrt{-120}}4[/latex]

Solve using the Quadratic Formula.

  1. [latex]6x^2-11x=35[/latex]
  2. [latex]52.2x^2-26.37x-15.3=0[/latex]
  3. [latex]3x^2-5x-7=0[/latex]
  4. [latex]16x^2=2[/latex]
  5. [latex]-x^2+8x=10[/latex]
  6. [latex]2x^2+8=-3x+\frac12[/latex]
  7. [latex]x^2-\frac23x+8=0[/latex]
  8. [latex]-5x^2+10x-5=0[/latex]
  9. [latex]-x^2+5x-2=0[/latex]
  10. [latex]3x^2-6x=0[/latex]
  11. Explain how you can tell from the Quadratic Formula whether [latex]f\left(x\right)=ax^2+bx+c[/latex] has one, two, or no real x-intercepts?
  12. Spot the error and correct it.

[latex]x=\frac{2\pm\sqrt{121}}4[/latex]

A Student’s Answer:[latex]\frac{2\pm11}4[/latex]

  1. Spot the error and correct it.

    [latex]x^2+20=4[/latex]

    [latex]x^2+20-4=0[/latex]

    [latex]a=1\;\;b=20\;\;c=-4[/latex]

Graph and identify the following characteristics for the function.

  1. [latex]g\left(x\right)=-2x^2+12x-15[/latex]

    Opens: Up / Down

    Axis of Symmetry:

    Vertex:

    y-intercept:

    x-intercept(s):

    Domain:

    Range:

Answer the following.

  1. At t seconds, the height h, in feet, of a baseball pitched into the air is given by the function below

    [latex]h\left(t\right)=-16t^2+20t+8[/latex]

    When does the ball hit the ground?

  2. When Greg dives off a diving board, his height h (in feet) above the water is modeled by the function: [latex]h\left(t\right)=-16t^2+15t+12[/latex], where t is in seconds. Find the time it will take for Greg to hit the water.
  3. An astronaut on the Moon throws a baseball upward with an initial velocity of 10 meters per second, releasing the baseball 2 meters above the ground. The height of the baseball (in meters) is modeled by the function: [latex]h\left(t\right)=-0.81t^2+10t+2.[/latex] The same experiment done on Earth is modeled by [latex]h\left(t\right)=-4.9t^2+10t+2,[/latex] where h is in meters. How much longer would the ball stay in the air on the Moon compared to on Earth?
  4. Hector throws a rock from the top of a tall building. The distance, in feet, between the rock and the ground t seconds after it is thrown is given by [latex]d\left(t\right)=-16t^2-4t+382[/latex].
    1. How long after the rock is thrown is it 310 feet from the ground?
    2. How tall is the building?
    3. Write a reasonable domain and range for this situation.
    4. Graph the function.

License

College Algebra for Non-STEM Majors Copyright © by Amy Collins Montalbano. All Rights Reserved.

Share This Book