3.2 Rational Functions
3.2.1 Prep
Determine whether the fraction is 0 or undefined.
- [latex]\frac70[/latex]
- [latex]\frac08[/latex]
- [latex]-\frac{(4-9)}{(6-6)}[/latex]
- [latex]\frac{(-4+9)}{3-9}[/latex]
Decide if the equation is linear or quadratic, then find all values of x which make it true.
- [latex]x-7\;=\;0[/latex]
- [latex]x\;+\;3\;=\;0[/latex]
- [latex]2x\;-\;9\;=\;0[/latex]
- [latex]-4x\;-\;7\;=\;0[/latex]
- [latex]x^2+2x+1=0[/latex]
- [latex]2x^2-x-1=0[/latex]
- [latex]2x^2+\;11x\;-\;21=0[/latex]
Answer the following.
- Graph [latex]x=2[/latex].
- What is the slope?
- What is the x-intercept?
- What is the y-intercept?
- Graph [latex]y=-3[/latex].
- What is the slope?
- What is the x-intercept?
- What is the y-intercept?
- Determine which of the following equations define vertical lines.
- [latex]x=5[/latex]
- [latex]y=5[/latex]
- [latex]2x=8[/latex]
- [latex]y-8=0[/latex]
- [latex]\frac23x+\frac12=1[/latex]
- [latex]\frac34y-2=-1[/latex]
- [latex]2x+3y=-2[/latex]
- [latex]7y=1[/latex]
- [latex]\frac x6+4=-5[/latex]
- [latex]x=0[/latex]
3.2.2 Classwork
Fill in the table for the function [latex]f(x)=\frac1x.[/latex] Then sketch the graph.
| [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}[/latex] | [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol f}\mathbf{\color[rgb]{1.0, 1.0, 1.0}\left(x\right)}[/latex] | [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}[/latex] | [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol f}\mathbf{\color[rgb]{1.0, 1.0, 1.0}\left(x\right)}[/latex] |
|---|---|---|---|
| [latex]1[/latex] | [latex]1[/latex] | ||
| [latex]0.5[/latex] | [latex]2[/latex] | ||
| [latex]0.25[/latex] | [latex]4[/latex] | ||
| [latex]0.2[/latex] | [latex]5[/latex] | ||
| [latex]0.125[/latex] | [latex]8[/latex] | ||
| [latex]0.1111[/latex] | [latex]9[/latex] | ||
| [latex]0.1[/latex] | [latex]10[/latex] |
- According to the table, what happens to the output f(x) as the input x gets smaller approaching 0?
- According to the table, what happens to the output f(x) as the input x gets larger approaching [latex]\infty[/latex]?
- Sketch the graph.
Find the vertical asymptote(s) and state the domain of the following functions.
- [latex]f(x)=\frac{2x^2+7}{x-6}[/latex]
- [latex]f(x)=\frac{2x+5}{x^2-6x-16}[/latex]
- [latex]f(x)=\frac{x^2-6x+9}{x^2-4}[/latex]
- [latex]y=\frac{2x+1}{8x-x^2}[/latex]
Write the equation of a rational function that satisfies the following requirements.
- A vertical asymptote at [latex]x=10[/latex].
- Vertical asymptotes at [latex]x=-5[/latex] and [latex]x=2[/latex].
- Domain: [latex]x\;\neq\pm5[/latex]
Solve.
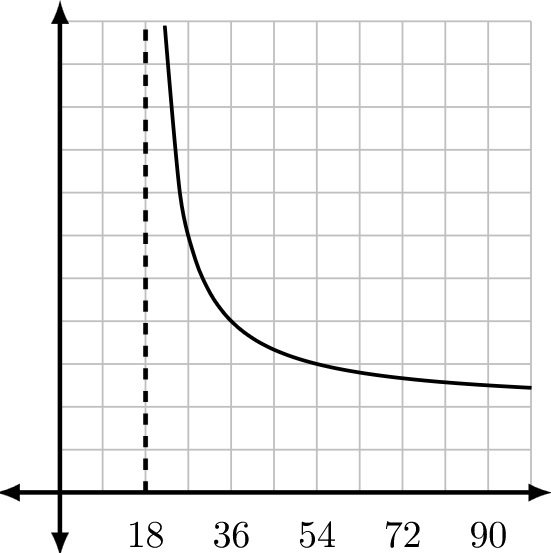
- Heavy metal contaminants in a cement quarry may be removed from the soil by planting sunflowers.
Use the following model to estimate the number of sunflowers S (in thousands) needed to remove p percent of the contamination.
(Note that p is a percent, so [latex]25\%[/latex] means [latex]p=25[/latex])[latex]S(p)=\frac{90}{100-p}[/latex]
- How many sunflowers would it take to remove 50% of the contamination?
- How many sunflowers would it take to remove 99% of the contamination?
- What percent removal cannot be achieved? Explain why not.
- It costs money to keep our lake at NVC clean. Say there are 2 tons of pollution in the lake and the cost C (in hundreds of dollars) of removing x tons of pollution is:
[latex]C(x)=\frac{70x}{2-x}[/latex]
- How much would it cost to remove half a ton of pollution?
- Explain what happens if NVC attempts to remove all 2 tons of pollution.
- A typical round of golf is 18 holes, where your cumulative score for the round is the sum of all shots you took on each hole. For example, if you took four shots on each hole, your score is: [latex]4(18)=72[/latex]
- Describe the relationship between the rounds of play and the score on 18 holes.
- Which scores are impossible, and why?
score on 18 holes
3.2.3 Homework
Find the vertical asymptote(s) and state the domain for the following functions.
- [latex]y=\frac{6x+36}{3x-10}[/latex]
- [latex]f(x)=\frac{3x^2+5}{x^2-16}[/latex]
- [latex]y=\frac{x-5}{5x}[/latex]
- [latex]g(x)=\frac{2x+5}{x^2-4x-5}[/latex]
Write the equation of a rational function that satisfies the following requirements:
- A vertical asymptote at [latex]x=-\frac32[/latex]
- Domain: [latex]x\neq\;-\frac13,\;4[/latex]
Explain.
- Explain in your own words why you cannot divide by zero.
- Explain in your own words what happens to the output of a rational function when the input approaches a vertical asymptote.
Solve.
- When traveling at a constant speed, d=rt, where d is distance, r is rate (or speed), and t is time.
- Solve for t.
- How long will it take to drive 195 miles if you average 60 miles per hour? (Answer in hours and minutes.)
- According to (a), what happens to time if your speed approaches 0 miles per hour?
- Suppose it costs C dollars (in billions) to build x miles of a wall along the US-Mexico border, given by the function:
[latex]C(x)=\frac{0.425x}{1954-x}[/latex]
- Approximate (to the nearest million) how much it would cost to build 1000 miles of such a wall.
- According to this model, how many miles of wall would be impossible to build? Explain.
- The Ideal Gas Law is PV=nRT, where P is pressure, V is volume, T is absolute temperature, n is the number of moles of gas, and R is a constant 8.314 J/K·mol (Joules per Kelvin per mole). Thus, [latex]PV=n\left(8.314\right)T[/latex]
- Solve for P.
- According to (a), what happens to pressure as volume increases?
- According to (a), what happens to pressure as volume decreases?
- What value for the volume of gas can never be attained, and why?
- Charles’ Law states that when a gas is held under constant pressure, the volume of the gas is directly proportional to the Kelvin temperature. That is,
[latex]\frac{V_1}{T_1}=\frac{V_2}{T_2},[/latex]
where [latex]V_1[/latex] is the initial volume, [latex]V_2[/latex] is the final volume, [latex]T_1[/latex] is the initial temperature, and [latex]T_2[/latex] is the final temperature. Both [latex]T_1[/latex] and [latex]T_2[/latex] must be measured in a temperature unit Kelvin, K, not degrees Celsius or Fahrenheit.
[latex]K = {}^{\circ}C + 273 \quad \quad {}^{\circ}C = \frac{5}{9} ( {}^{\circ}F - 32)[/latex]
- Five liters of a gas have a temperature of 250 K. If the previous temperature was 300 K, what was its volume?
- 3.1 cubic meters of a gas have a temperature of 15°C. What temperature is required to increase the volume to 3.5 cubic meters?
- 1,300 cubic inches of a gas are at a temperature of 78°F. If the temperature increases to 90°F, what is the new volume?
- 7 liters of a gas are at an air temperature of 300 K. Six hours later, the volume was measured at 7.2 liters. What is the new air temperature? Express the answer in Celsius.

