3.3 Exponential Functions
3.3.1 Prep
Convert the percents to decimals.
- [latex]65\%[/latex]
- [latex]10.5\%[/latex]
- [latex]0.25\%[/latex]
- [latex]8\frac34\%[/latex]
- [latex]0.0045\%[/latex]
- [latex]7\frac35\%[/latex]
- [latex]-0.035\%[/latex]
Match each expression to the correct definition.
-
_________ [latex]x^3[/latex]
_________ [latex]3x[/latex]
_________ [latex]\frac13x[/latex]
_________ [latex]x-3[/latex]
_________ [latex]x+3[/latex]
_________ [latex]3^x[/latex]
- 3 multiplied by itself x number of times
- A number divided by 3
- 3 less than a number
- A number multiplied by itself 3 times
- 3 more than a number
- A number multiplied by 3
- Discuss whether [latex]10^x[/latex] is the same as [latex]x^{10}[/latex]. Try substituting several different values for x to support your answer.
Answer the following.
- Steve wants to invest [latex]\$500[/latex] this month in an account that earns [latex]1.07\%[/latex] interest. If he leaves his money in the account, how much will he have in 5 years?
- What is the interest rate as a percentage? As a decimal?
- How much does Steve want to invest?
- How long is Steve leaving his money in the account?
- Steve wants to invest [latex]\$500[/latex] this month in an account that earns [latex]1.07\%[/latex] interest. If he leaves his money in the account, how much will he have in 5 years if the money is compounded weekly?
What additional information was given in this question that was not given in the previous question? - Miranda is going to invest her money in an account that earns [latex]1.25\%[/latex] interest, compounded monthly. If she leaves her money in the account for 16 months, how much will she have at the end of 16 months?
- What is the interest rate as a percentage? As a decimal?
- How long is Miranda leaving her money in the account? Answer in months, then years.
- Samantha is going to invest [latex]\$100[/latex] for 15 months at [latex]2\frac12\%[/latex] interest rate. How much money will she have if it is compounded weekly?
- What is the interest rate as a percentage? As a decimal?
- How long is Samantha leaving her money in the account? Answer in months, then years.
3.3.2 Preview
Example
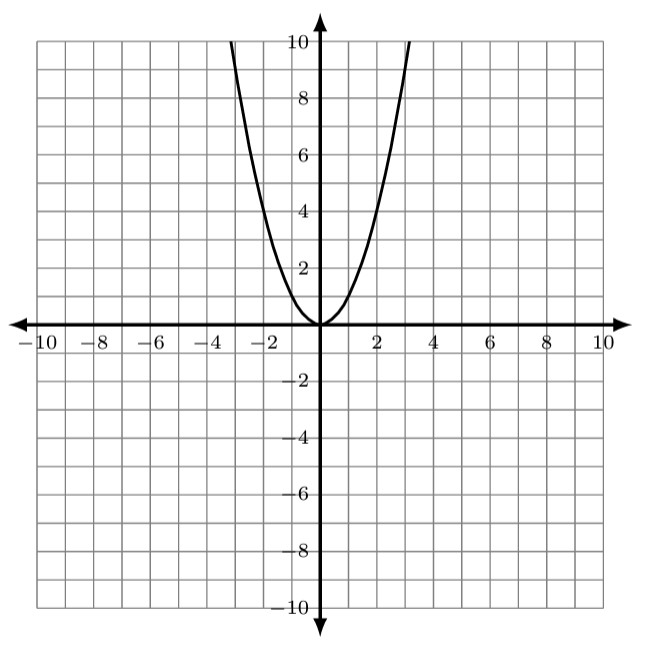
The graph of the quadratic function [latex]f(x)=x^2[/latex] is shown below.
| [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}[/latex] | [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol y}{\color[rgb]{1.0, 1.0, 1.0}\mathbf=}{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}^{\color[rgb]{1.0, 1.0, 1.0}\mathbf2}[/latex] |
|---|---|
| [latex]-2[/latex] | [latex]4[/latex] |
| [latex]-1[/latex] | [latex]1[/latex] |
| [latex]0[/latex] | [latex]0[/latex] |
| [latex]1[/latex] | [latex]1[/latex] |
| [latex]2[/latex] | [latex]4[/latex] |
| [latex]3[/latex] | [latex]9[/latex] |
| [latex]4[/latex] | [latex]16[/latex] |
| [latex]5[/latex] | [latex]25[/latex] |
| [latex]6[/latex] | [latex]36[/latex] |
An exponential function is modeled by:
where the exponent x is a variable, the base b is positive [latex](b>0)[/latex] but [latex]b\neq1[/latex].
Example
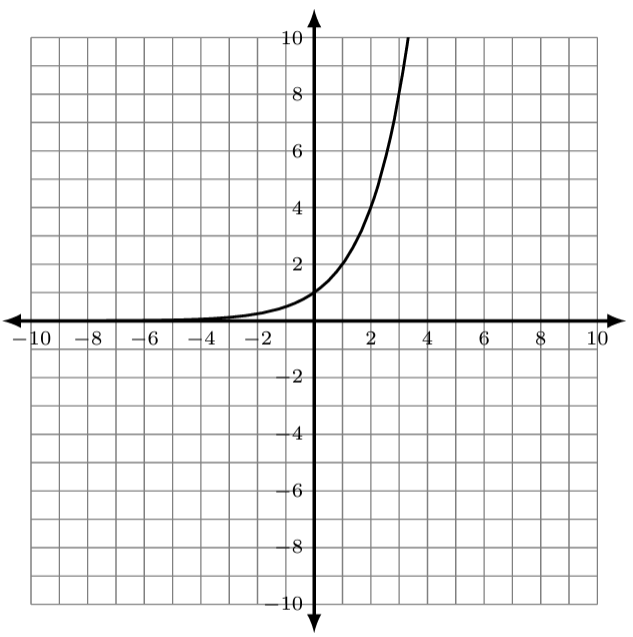
The graph of the exponential function [latex]g(x)=2^x[/latex] is shown below.
| [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}[/latex] | [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol y}{\color[rgb]{1.0, 1.0, 1.0}\mathbf=}{\color[rgb]{1.0, 1.0, 1.0}\mathbf2}^{\color[rgb]{1.0, 1.0, 1.0}\mathbf x}[/latex] |
|---|---|
| [latex]-2[/latex] | [latex]\frac{1}{4}[/latex] |
| [latex]-1[/latex] | [latex]\frac{1}{2}[/latex] |
| [latex]0[/latex] | [latex]1[/latex] |
| [latex]1[/latex] | [latex]2[/latex] |
| [latex]2[/latex] | [latex]4[/latex] |
| [latex]3[/latex] | [latex]8[/latex] |
| [latex]4[/latex] | [latex]16[/latex] |
| [latex]5[/latex] | [latex]32[/latex] |
| [latex]6[/latex] | [latex]64[/latex] |
Try It!
Which of these functions is growing faster for larger positive values of x?
The next section will involve the study of exponential growth or decay.
Compound Interest Formula
A = final amount
P = principal (initial amount)
r = rate (expressed as a decimal)
n = total number of compounding times in a year
t = time
Example
The number [latex]\pi[/latex] is a mathematical constant that appears throughout mathematics and physics. When rounded to five decimal places, [latex]\pi\approx3.14159[/latex]. The number e is another mathematical constant sometimes called the natural base or Euler’s number. When rounded to five decimal places, [latex]e\approx2.71828[/latex].
The natural exponential function is given by [latex]f(x)=e^x[/latex] and is graphed below.
| [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}[/latex] | [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol y}{\color[rgb]{1.0, 1.0, 1.0}\mathbf=}{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol e}^{\color[rgb]{1.0, 1.0, 1.0}\mathbf x}[/latex] |
|---|---|
| [latex]-3[/latex] | [latex]0.04979[/latex] |
| [latex]-2[/latex] | [latex]0.13534[/latex] |
| [latex]-1[/latex] | [latex]0.36788[/latex] |
| [latex]0[/latex] | [latex]1[/latex] |
| [latex]1[/latex] | [latex]2.71828[/latex] |
| [latex]2[/latex] | [latex]7.38906[/latex] |
| [latex]3[/latex] | [latex]20.08554[/latex] |

Continuous Compound Interest Formula
A = final amount
P = principal (initial amount)
r = rate (expressed as a decimal)
t = time
3.3.3 Classwork
Graph each of the following functions and write the domain, range, and y-intercept.
-
[latex]f(x)=2^x[/latex]
Domain:
Range:
y-intercept:
-
[latex]f(x)=5^x[/latex]
Domain:
Range:
y-intercept:

-
[latex]f(x)=3^{-x}[/latex]
Domain:
Range:
y-intercept:

Exponential Models
Simple Interest formula
Compound Interest formula
Definitions:
A =
P =
r =
t =
n =
Number of Compounding Times
| Annually | n = |
|---|---|
| Semiannually | n = |
| Quarterly | n = |
| Monthly | n = |
| Weekly | n = |
Continuous Compound Interest formula
Solve.
- You have invested [latex]\$100[/latex] earning [latex]2\%[/latex] interest. How much will this be worth in 15 years if interest is:
- Simple?
- Compounded annually?
- Compounded monthly?
- Compounded weekly?
- Compounded continuously?
- If you invest [latex]\$800[/latex] for 5 years at [latex]2\frac12\%[/latex] interest, how much would you end up with if interest is:
- Simple?
- Compounded annually?
- Compounded monthly?
- Compounded weekly?
- Compounded hourly?
- Compounded continuously?
- The growth of a bacteria colony can be modeled by the function below, where N is the number of bacteria (in thousands) and t is the time in minutes.
[latex]N=25e^{kt}[/latex]
- What is the initial population of bacteria?
- If the growth rate is [latex]1\%[/latex] per minute, how many bacteria would you have after 2 hours?
- Suppose that [latex]\$7000[/latex] is invested at an annual interest rate of [latex]5\%[/latex], compounded daily. Find the total amount in the account after 12 years if no withdrawals are made.
- Suppose that [latex]\$10,000[/latex] is invested at an annual interest rate of [latex]4\frac14\%[/latex], compounded continuously. Find the total amount in the account after 35 years if no withdrawals are made.
- An investment property in 2016 was worth [latex]\$3,75,000[/latex]. If it decreased in value at a rate of [latex]3.5\%[/latex] a year (compounded annually), what will it be worth in 2030?
- Tim is trying to decide which loan is better. Bank A offers a 15-year loan at a rate of [latex]4.5\%[/latex] compounded weekly, while Bank B offers a 10-year loan at a rate of [latex]5.75\%[/latex] compounded continuously. Tim wants the loan that will result in the lowest total owed. If he is borrowing [latex]\$4,800[/latex], which loan should he take?
- The amount of plutonium remaining from 1 kilogram after x years is given by the function
[latex]W\left(x\right)=2^{-x/24,360}[/latex]- How much will be left after 1,000 years?
- How much will be left after 10,000 years?
- The function [latex]M(h)=10e^{-0.173h}[/latex] can be used to find the number of milligrams M of morphine that is in the patient’s bloodstream h hours after the drug has been administered.
- What was the initial dosage?
- How many milligrams will be present after 1 hour? After 4 hours?
3.3.4 Homework
Graph each of the following functions and write the domain, range, and y-intercept.
-
[latex]f(x)=3^x[/latex]
Domain:
Range:
y-intercept:

-
[latex]f(x)=6^x[/latex]
Domain:
Range:
y-intercept:

- Describe when to use [latex]A=P\left(1+\frac rn\right)^{nt}[/latex] versus [latex]A=Pe^{rt}[/latex].
- Can the output of [latex]f(x)=5^x[/latex] ever be a negative number? Why or why not?
Solve.
- Suppose that [latex]\$7,000[/latex] is invested at an interest rate of [latex]6\%[/latex], compounded continuously. Find the amount in the account after 5 years if no withdrawals are made.
- Suppose that [latex]\$1,000[/latex] is invested at an interest rate of [latex]7\frac34\%[/latex], compounded semiannually. Find the amount in the account after 10 years if no withdrawals are made.
- Suppose that [latex]\$1,000[/latex] is invested at an annual interest rate of [latex]8\%[/latex], compounded quarterly. Find the total amount in the account after 10 years if no withdrawals are made.
- If [latex]\$15,000[/latex] is invested at an annual interest rate of [latex]3.5\%[/latex], compounded continuously, find the total amount in the account at the end of 6 years. Assume no withdrawals are made.
- An investment property in 1997 was worth [latex]\$250,000[/latex]. If it increased in value at a rate of [latex]12\%[/latex] compounded annually, what was it worth in 2005?
- George is trying to decide which loan is better. Both lending institutions offer loans based on continuous compounding. The first one offers a five-year loan at a rate of [latex]5.75\%[/latex], while the second offers a four-year loan at a rate of [latex]5.8\%[/latex]. George wants the loan that will result in the lowest total owed. If he is borrowing [latex]\$3,000[/latex], which loan should he take?
- When the Fukushima nuclear plant in Japan melted on March 12-15, 2011, it subsequently released approximately 511,000 terabecquerel (TBq) of Iodine-131 (I-131) into the atmosphere and surrounding Pacific Ocean. The amount of this radioactive material now remaining can be modeled by the function [latex]I(t)=511\cdot 2^{-\frac t8}[/latex], where I is in thousands of TBq and t is in days.
- How much I-131 was left from the accident one year later?
- Approximate how much I-131 will be left after 10,000 years?
- Approximate how much I-131 is left today.
- The function [latex]D(h)=5e^{-0.4h}[/latex] can be used to find the number of milligrams D of a certain drug that is in the patient’s bloodstream h hours after the drug has been administered. How many milligrams will be present after 1 hour? After 6 hours?

