3.4 Inverse Functions
3.4.1 Prep
Fill in the tables and sketch the two functions on the same graph.
- [latex]f(x)=2x[/latex]
[latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}[/latex] [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol y}{\color[rgb]{1.0, 1.0, 1.0}\mathbf=}{\color[rgb]{1.0, 1.0, 1.0}\mathbf2}{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}[/latex] [latex]-2[/latex] [latex]-1[/latex] [latex]0[/latex] [latex]1[/latex] [latex]2[/latex] [latex]3[/latex] 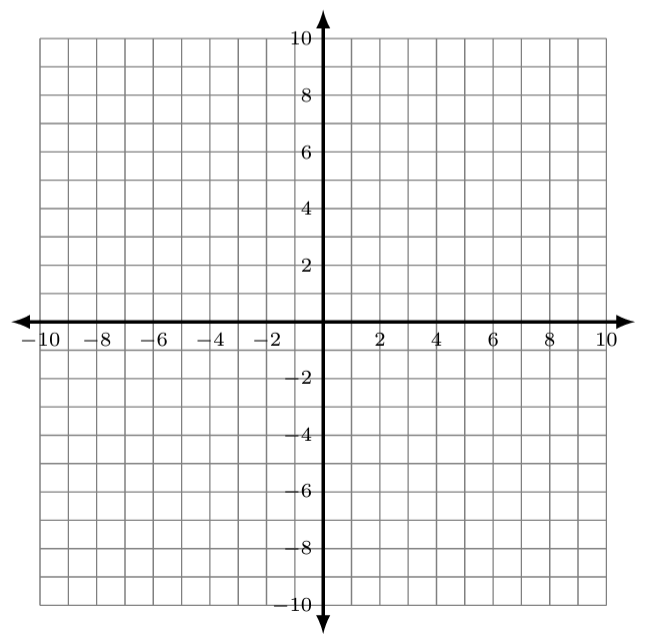
- [latex]g(x)=\frac x2[/latex]
[latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}[/latex] [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol y}{\color[rgb]{1.0, 1.0, 1.0}\mathbf=}{\color[rgb]{1.0, 1.0, 1.0}\frac{\mathbf x}{\mathbf2}}[/latex] [latex]-4[/latex] [latex]-2[/latex] [latex]0[/latex] [latex]2[/latex] [latex]4[/latex] [latex]6[/latex] - How are the x- and y-coordinates of the two functions related?
Simplify
- [latex]x+5-5[/latex]
- [latex]6\left(\frac x6\right)[/latex]
- [latex]\frac{3x}3[/latex]
- [latex]x-2+2[/latex]
- [latex]\sqrt{4^2}[/latex]
- [latex]\sqrt{6^2}[/latex]
- [latex]\sqrt{2^2}[/latex]
- [latex]\sqrt{8^2}[/latex]
Convert the following percents to decimals.
- [latex]45\%[/latex]
- [latex]18.25\%[/latex]
- [latex]0.15\%[/latex]
- [latex]12\frac9{10}\%[/latex]
- [latex]0.005\%[/latex]
- [latex]-2{\frac1{5}}\%[/latex]
- [latex]-0.269\%[/latex]
Answer the following.
- [latex]\$7,000[/latex] is invested at [latex]8.5\%[/latex]. How long will it take the investment to grow to [latex]\$10,000[/latex] if it is compounded continuously?
- How much money is being invested?
- What is the interest rate as a percent? As a decimal?
- What is the final amount of money (balance)?
- What is the unknown you are asked to find?
- [latex]\$7,000[/latex] is invested at [latex]8.5\%[/latex]. How long will it take the investment to double, if it is compounded continuously?
- How does this problem differ from the previous one?
- What is the unknown you are asked to find?
- What interest rate is needed to begin with [latex]\$1,000[/latex] and end with [latex]\$1,245[/latex] if the money is compounded continuously for 6 years?
- How much money is being invested (principal)?
- What is the final amount of money (balance)?
- What is the unknown you are asked to find?
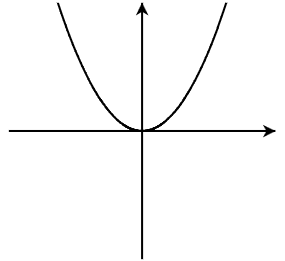
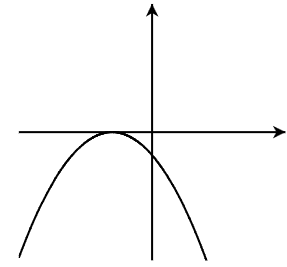
Match the function description to a possible graph.
-
-
List Start From 22
_____________ Linear, [latex]m>0[/latex] (A)
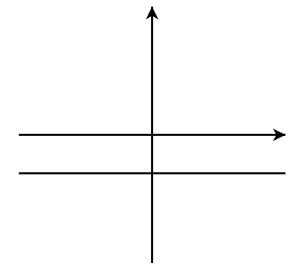
_____________ Linear, m<0 (B)
_____________ Linear, [latex]m=0[/latex] (C)
_____________ Linear, m is undefined (D)
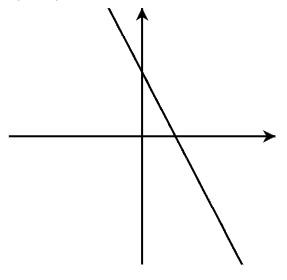
_____________ Quadratic, a<0 (E)
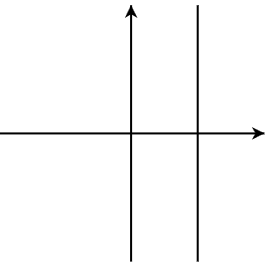
_____________ Quadratic, [latex]a>0[/latex] (F)
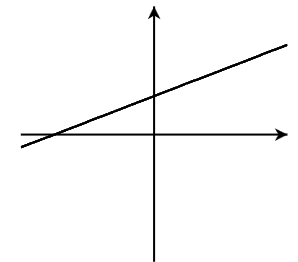
-
3.4.2 Preview
Remember that to solve an equation for x, we apply steps to undo any operations attached to x. For example, we use subtraction to undo addition and division to undo multiplication.
Try It!
What is the "undo" for each of the following?
- opening a door
- turning on the oven
- driving forward
- adding 5
- multiplying by 5
Try It!
Set up an equation for the following scenario. Identify the unknown variable, but do not solve.
"[latex]\$7,000[/latex] is invested at [latex]8.5\%[/latex]. How long will it take the investment to grow to [latex]\$10,000[/latex] if it is compounded continuously?"
Try It!
Fill in the tables and sketch the two functions on the same graph.
[latex]f(z)=4x[/latex]
| [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}[/latex] | [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol y}{\color[rgb]{1.0, 1.0, 1.0}\mathbf=}{\color[rgb]{1.0, 1.0, 1.0}\mathbf4}{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}[/latex] |
|---|---|
| [latex]-2[/latex] | |
| [latex]-1[/latex] | |
| [latex]0[/latex] | |
| [latex]1[/latex] | |
| [latex]2[/latex] |

[latex]g(x)=\frac14x[/latex]
| [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}[/latex] | [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol y}{\color[rgb]{1.0, 1.0, 1.0}\mathbf=}{\color[rgb]{1.0, 1.0, 1.0}\frac{\mathbf1}{\mathbf4}}{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}[/latex] |
|---|---|
| [latex]-8[/latex] | |
| [latex]-4[/latex] | |
| [latex]0[/latex] | |
| [latex]4[/latex] | |
| [latex]8[/latex] |
How are the x- and y-coordinates of these two functions related?
3.4.3 Classwork
Fill in the tables and sketch the two functions on the same graph.
- [latex]f(x)=x^2,\;x\geq0[/latex]
[latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}[/latex] [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol y}{\color[rgb]{1.0, 1.0, 1.0}\mathbf=}{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}^{\color[rgb]{1.0, 1.0, 1.0}\mathbf2}[/latex] [latex]0[/latex] [latex]\frac13[/latex] [latex]\frac12[/latex] [latex]1[/latex] [latex]2[/latex] [latex]3[/latex] 
- [latex]g(x)=x^\frac12\quad(note:\;x^\frac12=\sqrt x)[/latex]
[latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}[/latex] [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol y}{\color[rgb]{1.0, 1.0, 1.0}\mathbf=}{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}^{\color[rgb]{1.0, 1.0, 1.0}\frac{\mathbf1}{\mathbf2}}[/latex] [latex]0[/latex] [latex]\frac19[/latex] [latex]\frac14[/latex] [latex]1[/latex] [latex]4[/latex] [latex]9[/latex] - How are the x- and y-coordinates of the square and square root functions related?
Solve the equations.
- [latex]x^\frac12=3[/latex]
- [latex]x^2=9,\;x>0[/latex]
Recap:
- What is the main idea behind inverse functions?
- What is the relationship between x- and y-coordinates of inverse functions?
- How are the graphs of inverse functions related?
- How are the domain and range of inverse functions related?

