"

4.1 Substitution and Elimination

4.1.1 Prep

A. Answer the following.

    1. Find one solution for [latex]x+2=10[/latex]
    2. Determine how many solutions are possible.
    3. Graph [latex]x+2=10[/latex]
      A number line with integers marked from -8 to 8.
    1. Find one solution for [latex]x+y=5[/latex]
    2. Determine how many solutions are possible.
    3. Graph [latex]x+y=5[/latex]
      A Cartesian coordinate system is shown with a grid. The horizontal x-axis ranges from -8 to 8, with integer markings. The vertical y-axis also ranges from -8 to 8, with integer markings. The x and y axes intersect at the origin (0, 0).
    1. Find one solution for [latex]\left\{\begin{array}{l}x+y=5\\2x-y=1\end{array}\right.[/latex]
    2. Determine how many solutions are possible.
    3. Graph [latex]\left\{\begin{array}{l}x+y=5\\2x-y=1\end{array}\right.[/latex]
      A Cartesian coordinate system is shown with a grid. The horizontal x-axis ranges from -8 to 8, with integer markings. The vertical y-axis also ranges from -8 to 8, with integer markings. The x and y axes intersect at the origin (0, 0).

B. Match the equivalent equations.

  1. [latex]\;\_\_\_\_\_\_\_\_\_\_\_\_\_\_\;x+y=\mathbf6[/latex]

    [latex]\;\_\_\_\_\_\_\_\_\_\_\_\_\_\_\;\mathbf3x-4y=1[/latex]

    [latex]\;\_\_\_\_\_\_\_\_\_\_\_\_\_\_\;-y=\mathbf3x-9[/latex]

    [latex]\;\_\_\_\_\_\_\_\_\_\_\_\_\_\_\;y=\mathbf2x-7[/latex]

    1. [latex]\mathbf6y-\mathbf{12}x=-42[/latex]
    2. [latex]\mathbf3x+\mathbf3y=\mathbf{18}[/latex]
    3. [latex]y=-\mathbf3x+\mathbf9[/latex]
    4. [latex]\frac32x-\mathbf2y=\frac12[/latex]

C. Multiply each equation by the given constant.

  1. Multiply [latex]3x-2y=8[/latex] by 7 on each side. The result is _____________.
  2. Multiply [latex]2x-\frac13y=9[/latex] by 3 on each side. The result is _____________.
  3. Multiply [latex]\frac45x-2=-8[/latex] by -5 on each side. The result is _____________.
  4. Multiply [latex]\frac{-3}7x=-y-8[/latex] by 2 on each side. The result is _____________.

D. Solve for y.

  1. [latex]2y=3x+8[/latex]
  2. [latex]-3y=3x-9[/latex]
  3. [latex]2x+3y=15[/latex]
  4. [latex]3x-3y=9[/latex]
  5. [latex]2x+2y=8[/latex]
  6. [latex]-y=2x+1[/latex]
  7. [latex]\frac12x-\frac23y=4[/latex]
  8. [latex]\frac45x-y=10[/latex]
  9. [latex]\frac12x+2y=6[/latex]

E. For each scenario, identify the two unknowns and assign them variables. The first one is already completed.

  1. A test has twenty questions worth one hundred points. The test has fill-in-the-blank questions that are worth three points each, and multiple choice questions that are worth eleven points each. How many multiple choice questions are there?
    x = the number of fill-in-the-blank questions
    y = the number of multiple choice questions
  2. A nurse is ordering two different kinds of medicine. Medicine A costs $7.00 per gram, and medicine B costs $9.75 per gram. The total bill is $268.50 and a total of 36 grams are ordered. How much of each medicine is ordered?
  3. Boxes of fruit can be purchased in large or small boxes. If 3 small boxes and 14 large boxes are purchased for a total of $203 on one day, and 11 small boxes and 11 large boxes are purchased for a total of $220 on another day, how much does a large box of fruit cost?
  4. The admission fee at a small fair is $1.50 for children and $4.00 for adults. On a certain day, 2200 people enter the fair and $5050 is collected. How many children and how many adults attended?

4.1.2 Preview

Try It!

  1. Find one solution for [latex]x-3=5[/latex]
  2. Determine how many solutions are possible. [latex][/latex]
  3. Graph [latex]x-3=5[/latex]
    A number line with integers marked from -8 to 8.

Try It!

Type your exercises here.

  1. Find one solution for [latex]x-y=6[/latex]
  2. Determine how many solutions are possible. [latex][/latex]
  3. Graph [latex]x-y=6[/latex]
    A Cartesian coordinate system is shown with a grid. The horizontal x-axis ranges from -8 to 8, with integer markings. The vertical y-axis also ranges from -8 to 8, with integer markings. The x and y axes intersect at the origin (0, 0).

A system of linear equations is a set of two or more linear equations.

Example

The following is a system of two linear equations in two variables, x and y.

[latex]\left\{\begin{array}{l}x-y=6\\x+y=2\end{array}\right.[/latex]

A solution of this system is an ordered pair [latex]\left(x,y\right)[/latex] that makes both equations true statements. For this system, [latex]\left(4,-2\right)[/latex] is a solution.

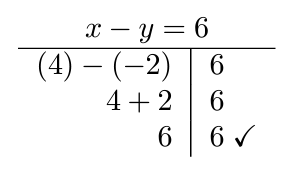
A mathematical check of the equation x-y=6 for a potential solution. It demonstrates the substitution of x=4 and y=−2 into the equation, resulting in (4) -(-2), which simplifies to 4+2=6. The final line shows 6∣6 with a checkmark, indicating that the ordered pair (4, -2) is indeed a solution to the equation x-y=6.
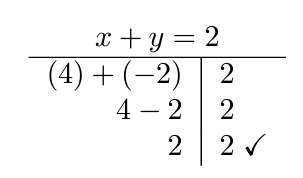
A verification of the equation x+y=2. It shows the substitution of values x=4 and y=-2 into the equation, leading to the expression (4) +(-2). This simplifies to 4-2=2. The final step confirms that 2 equals 2 with a checkmark, indicating that the values successfully satisfy the equation.

Example

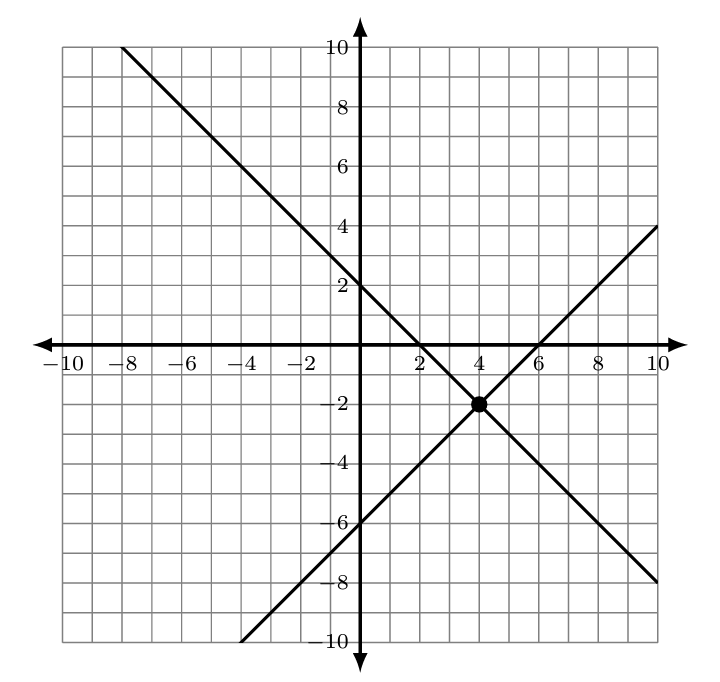
If both linear equations are graphed on the same axes, we see that each point at which the graphs intersect is a solution of both equations and therefore a solution of the system.

[latex]\left\{\begin{array}{l}x-y=6\\x+y=2\end{array}\right.[/latex]

This shows [latex]\left(4,-2\right)[/latex] is a solution.

Graph of two straight lines intersecting at the point (4,-2).

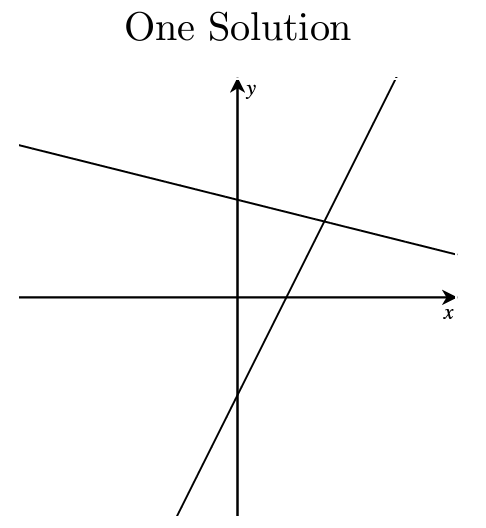
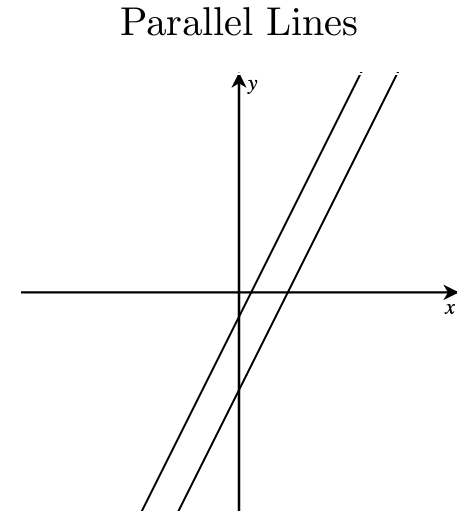
Fact: A system of linear equations has either:

  1. exactly one solution, or
  2. no solution, or
  3. infinitely many solutions.

    A graph on a Cartesian coordinate system titled "One Solution". It displays two distinct straight lines intersecting at a single point in the first quadrant.

    A graph on a Cartesian coordinate system, titled "Parallel Lines". It shows two distinct straight lines that are parallel to each other.

    A Cartesian coordinate system with a single straight line plotted, titled "Same Lines". The line has a positive slope and passes through the origin. The x and y axes are labeled.

4.1.3 Classwork

  1. Is [latex]\left(7,2\right)[/latex] a solution of the following system? Why or why not?
    [latex]\left\{\begin{array}{l}x-y=5\\2x+y=1\end{array}\right.[/latex]
  2. Solve the system using a valid algebraic approach.
    1. [latex]\left\{\begin{array}{l}2x-y=0\\3x+5y=39\end{array}\right.[/latex]
    2. [latex]\left\{\begin{array}{l}3x+2y=3\\4x-5y=-19\end{array}\right.[/latex]
    3. [latex]\left\{\begin{array}{l}2x-y=5\\-6x+3y=7\end{array}\right.[/latex]
    4. [latex]\left\{\begin{array}{l}3x+\frac13y=3\\\frac12x-\frac13y=-1\end{array}\right.[/latex]
  3. Solve.
    1. An animal shelter has 105 cats and dogs. They have 15 more dogs than cats. How many dogs do they have? How many cats?
    2. There were 429 people at a play. Admission was $8 each for adults and $4.50 each for children. The total receipts were $2,641. How many adults and how many children attended?
    3. You have a total $180. You have only $5 bills and $10 bills, and you have nine more tens than you have fives. How many of each bill do you have?
    4. A retired couple has $130,000 to invest to obtain annual income. They invest some in a safe certificate of deposit yielding 0.50% and the rest in riskier AA bonds yielding 1.10% per year. (Assume both yield simple interest.) How much should they invest in each to realize exactly $1,190 per year?

Matrices

  1. Determine the size of each matrix.

    [latex]\begin{aligned} A &= \begin{bmatrix} 1 & 6 \\ 4 & 0 \\ 0 & 2 \end{bmatrix} \quad B &= \begin{bmatrix} 5 & 7 \\ -1 & 8 \\ 10 & 1 \end{bmatrix} \quad C &= \begin{bmatrix} 0 & 3 & -2 \\ 1 & 10 & 5 \end{bmatrix} \quad D &= \begin{bmatrix} 1 \\ 4 \end{bmatrix} \end{aligned}[/latex]

  2. Write each system as an augmented matrix.
    1. [latex]\begin{align*} \left\{ \begin{aligned} 5x - 4y &= 9 \\ x - 2y &= -3 \end{aligned} \right. \end{align*}[/latex]
    2. [latex]\begin{align*} \left\{ \begin{aligned} 3x - 2y - 3z &= -5 \\ x + 2y + 3z &= -3 \\ -x + 4y - 6z &= -1 \end{aligned} \right. \end{align*}[/latex]
  3. Write the augmented matrix as a system of linear equations in variables [latex]x,y,[/latex] and [latex]z[/latex].[latex]\begin{align*} \left[ \begin{array}{ccc|c} 3 & -2 & 4 & 6 \\ 9 & 4 & -1 & 0 \\ 6 & -8 & -3 & 3 \end{array} \right] \end{align*}[/latex]
  4. Use the given matrix to write the solution for the corresponding linear system.
    [latex]\begin{align*} \left[ \begin{array}{cc|c} 1 & 0 & -7 \\ 0 & 1 & 4 \end{array} \right] \end{align*}[/latex]

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

College Algebra for Non-STEM Majors Copyright © by Northwest Vista College Mathematics Department is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book