"

4.2 Matrices

4.2.1 Preview

Example

Solve the system [latex]\left\{\begin{array}{l}x-2y=-1\\-x+3y=3\end{array}\right.[/latex]

Solution. Use the elimination method.

[latex]\;\;\;\begin{array}{rcccl}x&2y&=&1\\x&+3y&=&3\end{array}\quad\;\;\;\;\;\;\;\;\;\;\rightarrow\;\;\;\;\;\quad\begin{array}{rcl}x&2y&=1\\&y&=2\end{array}\quad\;\;\;\;\;\;\;\;\;\;\;\;\rightarrow\;\;\;\;\quad\begin{array}{rcl}x&&=3\\&y&=2\end{array}[/latex]


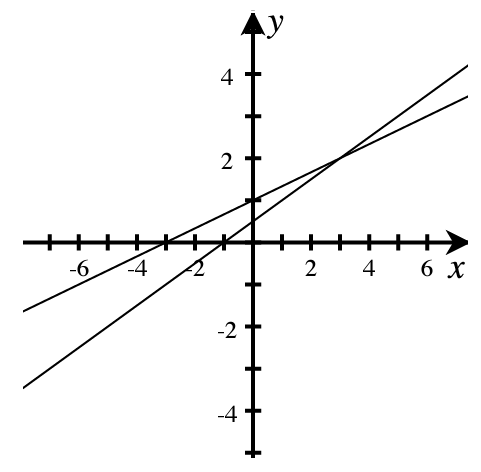
The solution is [latex]\left(3,2\right)[/latex]

Matrix Notation

A matrix is a rectangular array of numbers written within brackets. Each number is called an element.

[latex]\left\{\begin{array}{l}x-2y=-1\\-x+3y=3\end{array}\right.[/latex]

[latex]\begin{bmatrix}1&-2\\-1&3\end{bmatrix}[/latex]

(coefficient matrix)

[latex]\begin{bmatrix}-1\\3\end{bmatrix}[/latex]

(constant matrix)

Following the steps from the example above:

[latex]\begin{bmatrix}1&-2&-1\\-1&3&3\end{bmatrix}(\text{augmented}\;\text{matrix})\;\rightarrow\;\;\;\begin{bmatrix}1&-2&-1\\0&1&2\end{bmatrix}\;\;\rightarrow\;\;\;\begin{bmatrix}1&0&3\\0&1&2\end{bmatrix}(\text{The solution is})\;(3,2).[/latex]

The number of rows is m and the number of columns is n; they are called the dimensions of the matrix. The size of the matrix is m × n (read “m by n”). If m = n, the matrix is a square matrix.

[latex]2\times3[/latex]

[latex]\begin{bmatrix}2&-3&6\\8&1&-1\end{bmatrix}[/latex]

[latex]2\times2[/latex]

[latex]\begin{bmatrix}1&0\\0&1\end{bmatrix}[/latex]

(square matrix)

[latex]3\times3[/latex]

[latex]\begin{bmatrix}0.1&0.2&0.3\\0.4&0.5&0.6\\0.7&0.8&0.9\end{bmatrix}[/latex]

(square matrix)

[latex]4\times1[/latex]

[latex]\begin{bmatrix}0\\-1\\2\\3\end{bmatrix}[/latex]

(column matrix)

[latex]1\times5[/latex]

[latex]\begin{bmatrix}1&-\frac12&-1&-\frac13&6\end{bmatrix}[/latex]

(row matrix)

The position of an element is designated by its row and column written as subscripts, [latex]a_{ij}[/latex]. For example, [latex]a_{12}[/latex] refers to the element in the first row, second column.

[latex]\begin{bmatrix}2&-3&6\\8&1&-1\end{bmatrix}\;\;\;a_{12}=-3[/latex]

[latex]\begin{bmatrix}2&-2&1\\3&1&-1\\1&-3&2\end{bmatrix}\;a_{12}=-2[/latex]

One goal of this section it to write linear systems of the form:

[latex]\left\{\begin{array}{l}3x-5y=-8\\4x+3y=-1\end{array}\right.[/latex] or [latex]\left\{\begin{array}{l}4x+3y+z=-13\\3x-2y-z=-19\\4x+y+4z=-25\end{array}\right.[/latex]

Where x,y, and z are variables using their associated augmented matrics:

[latex]\begin{bmatrix}3&-5&-8\\-1&3&-1\end{bmatrix}[/latex] or [latex]\begin{bmatrix}4&3&1&-13\\3&-2&-1&-19\\4&1&4&-25\end{bmatrix}[/latex]

Example

The system [latex]\left\{\begin{array}{l}x-2y=3\\-4x+5y=6\end{array}\right.[/latex] is represented by the

augmented matrix [latex]\begin{bmatrix}1&-2&3\\-4&5&6\end{bmatrix}[/latex].

Try It!

Write the system as an augmented matrix.

[latex]\left\{\begin{array}{l}-x+8y=27\\\;\;\;\;\;\;\;\;3y=12\end{array}\right.[/latex]

4.2.2 Classwork

Determine the size of each matrix.

[latex]A=\begin{bmatrix}1&6\\4&0\\0&2\end{bmatrix}\;\;\;\;\;\;B=\begin{bmatrix}5&7\\-1&8\\10&1\end{bmatrix}\;\;\;\;\;\;\;\;\;C=\begin{bmatrix}0&3&-2\\1&10&5\end{bmatrix}\;\;\;\;\;\;\;\;\;D=\begin{bmatrix}1\\4\end{bmatrix}[/latex]

Write each system as an augmented matrix.

  1. [latex]\left\{\begin{array}{l}5x-4y=9\\x-2y=-3\end{array}\right.[/latex]
  2. [latex]\left\{\begin{array}{l}3x-2y-3z=-5\\x+2y+3z=-3\\-x+4y-6z=-1\end{array}\right.[/latex]

Write the augmented matrix as a system of linear equations in variables x, y, and z.

[latex]\begin{bmatrix}3&-2&4&6\\9&4&-1&0\\6&-8&-3&3\end{bmatrix}[/latex]

Use the given matrix to write the solution for the corresponding linear system.

[latex]\begin{bmatrix}1&0&-7\\0&1&4\end{bmatrix}[/latex]

4.2.3 Homework

Determine the size of the matrix.

    1. [latex]\begin{bmatrix}5&6\\1&4\\10&-2\\3&7\end{bmatrix}[/latex]

Solve the following systems using an algebraic or matrix method.

    1. [latex]\left\{\begin{array}{l}2x+3y=24\\7x+8y=64\end{array}\right.[/latex]
    2. [latex]\left\{\begin{array}{l}\frac16y=\frac12x+\frac13\\x-\frac13y=-1\end{array}\right.[/latex]
    3. [latex]\left\{\begin{array}{l}\frac x2+\frac y3=4\\\frac{3x}4+5y=33\end{array}\right.[/latex]
    4. [latex]\left\{\begin{array}{l}2x-3y=-8\\3x+5y=7\end{array}\right.[/latex]
    5. [latex]\left\{\begin{array}{l}\frac x2+\frac y4=\frac32\\\frac x5+\frac y{15}=\frac13\end{array}\right.[/latex]
    6. [latex]\left\{\begin{array}{l}x-4y=-25\\x+12y=10\end{array}\right.[/latex]
    7. [latex]\left\{\begin{array}{l}x+6y=9\\x+2y=-3\end{array}\right.[/latex]
    8. [latex]\left\{\begin{array}{l}8x+3y=24\\y=5x-3\end{array}\right.[/latex]

Solve.

    1. Myra is selling two types of candy bars for a school fundraiser, Sour Sillies and Choco Nuts. On the first day, she sold two Sour Sillies and four Choco Nuts for $10.00. On the second day she sold four Sour Sillies and two Choco Nuts for $11.00. Find the price for each type of candy bar.
    2. Tim Duncan of the San Antonio Spurs once scored 36 points on 22 shots in an NBA game, shooting only two-pointers and free throws (one-point). How many of each type of shot did he make?
    3. On a farm there are pigs and chickens. There are 7 more pigs than chickens, with a total of 58 feet. How many of each type of animal are there?
    4. The admission to a fundraiser is $5.00 for children and $7.50 for adults. On a certain day, 135 people attended the fundraiser, and $762.50 was collected. How many children and how many adults attended?
    5. A landscaper is designing a park and placed two orders with a nursery. The first order was for 13 trees and 4 bushes and totaled $1,075. The second order was for 6 trees and 2 bushes and totaled $500. What is the cost of one tree? What is the cost of one bush?
    6. A test has 20 questions worth 100 points. The test has True/False questions that are worth 3 points each, and multiple choice questions that are worth 11 points each. How many True/False questions are there?
    7. A nurse is ordering two different kinds of medicine. Medicine A costs $7.00 per gram, and Medicine B costs $9.75 per gram. The total bill is $268.50 and the nurse orders 24g more of Medicine A than Medicine B. How much of each medicine is ordered?
    8. Boxes of fruit can be purchased in large or small boxes. If 3 small boxes and 14 large boxes are purchased for a total of $203 on one day, and 11 small boxes and 11 large boxes are purchased for a total of $220 on another day, how much does a large box of fruit cost?

License

College Algebra for Non-STEM Majors Copyright © by Amy Collins Montalbano. All Rights Reserved.

Share This Book