"

1.1 Percents and Proportions

1.1.1 Prep

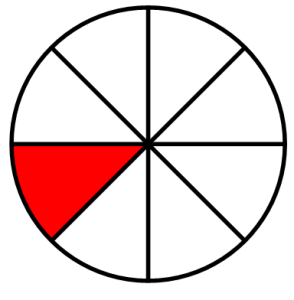
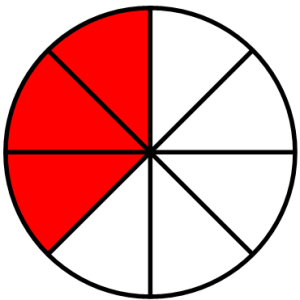
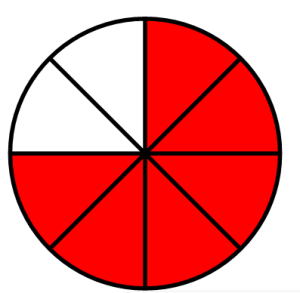
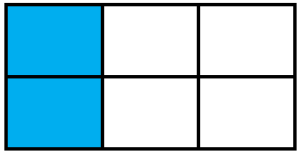
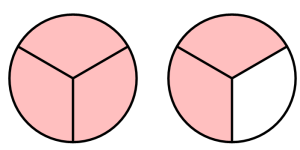
Write a ratio (fraction) that represents the shaded portion in each of the following figures. Determine which ratios are equivalent.

Discuss and answer the following.

  1. Draw a picture representing [latex]\frac14[/latex]. Draw a picture representing [latex]\frac41[/latex]. Are they equivalent?
  2. When is it necessary to write 1 in a ratio? Give other examples demonstrating when it is or is not necessary to write 1 in a ratio.

Identify the part from the whole. Then form the associated fraction.

  1. Tony tipped $8 on a $22.58 ticket.
  2. In an 82 game regular season, the Spurs won 58 games.
  3. NVC has 15,435 students. 4,630 of them will transfer to UTSA.
  4. Sam has caught 212 out of 802 Pokémon.
  5. My paycheck would have been $950, but $170 was taken out for income tax.
  6. Heidi is on a 5 hour car trip. She has driven 2 hours so far.

Answer the following.

  1. Identify how the following numbers and variables are held together – by addition, subtraction, multiplication, or division? For example, in the expression [latex]x+5[/latex], the variable and number are held together by addition.
    1. [latex]x-5[/latex]
    2. [latex]5\times x[/latex]
    3. [latex]5\times x[/latex]
    4. [latex]7+x[/latex]
    5. [latex]7\cdot x[/latex]
    6. [latex]-7+x[/latex]
    7. [latex]\frac x7[/latex]
    8. [latex]7x[/latex]
    9. [latex]\frac25x[/latex]
    10. [latex]p\cdot250[/latex]
    11. [latex]\frac2{100}\cdot x[/latex]
    12. [latex]\frac x{100}\cdot54[/latex]
    1. What operation do you use to undo addition?
    2. So then how would you solve [latex]x+5=19[/latex]?
    3. Try it! Solve [latex]x+20=75[/latex].
    1. What operation do you use to undo subtraction?
    2. So then how would you solve [latex]x-5=2[/latex]?
    3. Try it! Solve [latex]x-12=30[/latex].
    1. What operation do you use to undo multiplication?
    2. So then how would you solve [latex]3x=63[/latex]?
    3. Try it! Solve [latex]4x=88[/latex].
    1. Are [latex]x-3[/latex] and [latex]−3x[/latex] the same thing? Why or why not?
    2. How would you solve [latex]x-3=12[/latex]?
    3. How would you solve [latex]-3x=12[/latex]
    1. What operation does a fraction bar stand for?
    2. What operation do you use to undo this?
    3. So then how would you solve [latex]\frac x4=15[/latex]?
    4. Try it! Solve [latex]\frac x5=20[/latex]?
  2. What if there are numbers attached to a variable by both multiplication and division? Example: [latex]\frac25x=10[/latex] The 2 is attached by ______________, so undo the 2 by _____________.The 5 is attached by _____________, so undo the 5 by _____________. Try it! Solve [latex]\frac25x=10[/latex]
  3. What if the variable is in the denominator of a fraction? You can still undo this by using ____________. Try it! Solve [latex]\frac9x=45[/latex]
  4. What if both sides of the equations are fractions?Try it!Solve [latex]\frac9x=\frac{45}{100}[/latex]

Solve for the variable.

  1. [latex]p\cdot 250 = 25[/latex]
  2. [latex]0.45\cdot n=67.5[/latex]
  3. [latex]\frac{12}{100}\cdot x=624[/latex]
  4. [latex]\frac x{100}\cdot54=9.45[/latex]
  5. [latex]\frac7{20}=\frac x{60}[/latex]
  6. [latex]\frac{42}{75}=\frac x{100}[/latex]
  7. [latex]\frac{30}t=\frac5{3.4}[/latex]
  8. [latex]\frac{14}x=\frac{35}{10}[/latex]
  9. [latex]\frac{19}x=\frac{133}{21}[/latex]
  10. [latex]\frac{14}{16}=\frac7b[/latex]

1.1.2 Preview

A fraction (or ratio) is a number of the form [latex]\frac ab[/latex] where a is the numerator and b is the denominator.

For simplicity, a fraction may also be thought of as [latex]\frac{\text{Part}}{\text{Whole}}[/latex]

Example

The shaded region below represents the fraction [latex]\frac12[/latex] It may also be written as a decimal, 0.5, or as a percent, 50%.

[latex]\frac{{\text{Part}}}{{\text{Whole}}}=\frac12\;0.5=50\%[/latex]

“Per cent” means ÷100. Then 50% really means

[latex]50\%=50\div100=\frac{50}{100}=\frac12[/latex]

A ratio may only be expressed as a percent when the units of the numerator and the denominator are the
same. For example,

[latex]\frac{\$1}{2\;{\text{slices}}\;{\text{of}}\;{\text{pizza}}}\;{\text{cannot}}\;{\text{be}}\;{\text{written}}\;{\text{as}}\;{\text{a}}\;{\text{percent}}[/latex]

[latex]\frac{1\;{\text{slice}}\;{\text{of}}\;{\text{pizza}}}{2\;{\text{slices}}\;{\text{of}}\;{\text{pizza}}}=50\%\;{\text{of}}\;{\text{the}}\;{\text{pizza.}}[/latex]

Try It!

Express the given shaded region as a ratio, decimal, and percent.

A proportion is an equation of the form “Ratio = Ratio”. That is,

[latex]\frac AB=\frac CD[/latex]

Example

Suppose after you graduate from college, you start a job earning $21,500 over 6 months. If your pay stays at this rate, how much will you earn in 1 year? You can answer this question using a proportion.

[latex]\frac{\$21,\;500}{6\;{\text{months}}}=\frac x{12\;{\text{months}}}[/latex]

Multiply by 12 and solve for x.

[latex]\frac{\$21,\;500}{6\;{\text{months}}}=\frac x{12\;{\text{months}}}[/latex]

[latex]\frac{\$21,\;500}{\cancel{6\;{\text{months}}}}\cdot\cancel{12\;{\text{months}}}=\frac x{\cancel{12\;{\text{months}}}}\cdot\cancel{12\;{\text{months}}}[/latex]

[latex]\frac{\$21,\;500}{\cancel6}\cdot\cancelto{2}{12}=x[/latex]

[latex]\$21,500\cdot2=x[/latex]

[latex]\$43,000=x[/latex]

Therefore, you would earn $43,000 in 1 year.

Try It!

If you make $9,800 in 3 months, how much will you earn in one year?

1.1.3 Class Examples

Percent

Answer the following in your own words.

  1. Would you rather use a coupon worth $20 off your entire purchase or 20% of your entire purchase?
  2. Suppose someone leaves a $20 tip on a $200 check.
    1. Is this a good tip or a bad tip? Justify your answer using a percent.
    2. If you think it is a bad tip, what would be a better tip? Justify using a percent.

Write each of the following as equations and solve.

  1. What is 35% of 200?
  2. 35 is what percent of 200?
  3. 25 is 40% of what?
  4. 15% of a number is 19.5. Calculate that number.
  5. Thirty-five is fifteen percent of what value?
  6. Thirty percent of all students at NVC transfer to UTSA. Of these transfer students, 12% are going to major in Biology. If there are 15,435 students at NVC, how many will transfer to UTSA and major in Biology?
  7. Thirty percent of all students at NVC transfer to UTSA. Of these transfer students, 12% are going to major in Biology. What percent of NVC students are going to be at UTSA to major in Biology?
  8. In a Gallup poll of 976 adults, 68 said they drink alcohol every day. What is the percentage of respondents who said that they have a drink every day?

Proportions

Set up a proportion and solve.

  1. Joe’s heart beats 11 times in 10 seconds. At that rate, how many times does his heart beat in 60 seconds?
  2. One plain bagel has 320 calories. How many calories are in 2 and a half bagels?
  3. A leaking pipe can lose 24.7 gallons of water in a week. How many gallons are lost in 30 days?

Applications of Percent

Use the following equations to solve.

Price + (Price · Tax Rate) = Total

[latex]\frac{{\text{New}}\;-\;{\text{Old}}}{{\text{Old}}}\cdot100\;=\;\%\;{\text{Increase or Decrease}}[/latex]

  1. Amy bought a pool hall for $219,765. This price includes 5% state tax. What was the price of the pool hall before tax?
  2. Steve needs to buy his sister a birthday gift from the mall. He sees a shirt that is normally priced at $24.50, but it is on sale for 20% off. If the sales tax is 8.25%, how much will Steve pay for the shirt?
  3. Thomas is selling his Honda CR-V on consignment by leaving it with a dealer, who will get 25% of the selling price. What must the selling price be in order for Thomas’s share to be $1475?
  4. In 2004, Javier bought a new television set for $2500. In 2012, he purchased a similar model for $950. What was the percent decrease from 2004 to 2012? Round to the nearest 0.1%.
  5. The price of gas increased from $3.25 per gallon to $4.05 per gallon. What was the percent change to the nearest percent?

Mixtures

Solve.

  1. Mixing 1 gallon of 100% apple juice with 1 gallon of water, how much total liquid results and what percent is juice? What if you mix 3 gallons of juice with one gallon of water?
  2. If 2 cups of water from the Great Salt Lake of 10% salinity are mixed with 2 cups of swimming pool water of 0% salinity, how many cups result and what is the salinity of the mixture? (Estimate a reasonable percent range for your answer before you solve.)
  3. If you pour [latex]\frac23[/latex] cup of creamer (12% fat) into [latex]2\frac12[/latex] cups of coffee, how many cups result and what is the percent fat? (Estimate a reasonable percent range for your answer before you solve.)
  4. Twenty pints of a 2% saline solution is mixed with 15 pints of a 9% saline solution. How many pints are in the final mixture? What is the percent of saline in the final mixture? (Estimate a reasonable percent range for your answer before you solve.)
  5. There are 2 liters of 3% milk, which is mixed with some 1% low-fat milk. If there are 7 liters of the mixture, how many liters of 1% low-fat milk were there? What is the percentage of fat in this 7 liters of mixture? (Estimate a reasonable percent range for your answer before you solve.)

Mixed Practice

Solve.

  1. Assume there are 425 Statistics students at NVC, of which 35% plan to attend nursing school. If all of the students who plan to attend nursing school are enrolled in Statistics this semester, what percent of the 15,435 NVC student body plans to attend nursing school?
  2. A pre-election survey showed that 5 out of every 13 registered voters would vote in an election. At this rate, how many people would be expected to vote in a town of 5,850 registered voters?
  3. To estimate the number of trout in Big Bear Lake, a sample of 48 trout were captured and tagged. After releasing them, a net captured 300 trout, of which 9 were tagged. Estimate the number of trout in Big Bear Lake.
  4. Kelli takes her friends out to lunch and pays for the bill. Her friends insist on paying the tip. If the bill was $38.75, and they want to leave a 15% tip, how much money will they need to leave (bill plus tip)?
  5. If the Spurs finish the season with a record of 55 wins and 27 losses, what percent of their games will they have won? Write the answer to the nearest 0.1%.
  6. If the Spurs begin the season with a record of 7 wins and 4 losses, predict how many games they will win throughout the 82 games of the season.
    1. Set up as a percent and solve.
    2. Set up as a proportion and solve.

1.1.4 Homework

Write each of the following as equations and solve.

  1. Find 18% of 56.
  2. 36% of what number is 33.12?
  3. What percent of 54 is 17?
  4. What is 12% of 26?
  5. Would you rather use a 70% discount coupon or a 40% discount, 20% discount, then 10% discount coupon? Explain your answer.
  6. Yvette knows the names of 8% of the students at NVC. If there are 15,435 students at NVC, how many students does Yvette know by name?
  7. Mary has swim practice 20 out of 28 days in February. What percent of the month of February does Mary have swim practice? Round your answer to the nearest tenth of a percent.
  8. What is meant by a proportion?
  9. How do you solve a proportion?

Solve the following equations. When appropriate, round to three decimal places.

  1. [latex]\frac{30}t=\frac5{3.4}[/latex]
  2. [latex]\frac{14}x=\frac{35}{10}[/latex]
  3. [latex]\frac{19}x=\frac{133}{21}[/latex]
  4. [latex]\frac{8.6}{25.8}=\frac1k[/latex]
  5. [latex]\frac{14}{16}=\frac7b[/latex]

Set up a proportion and solve. When appropriate, round to two decimal places.

  1. Heidi walks at a rate of 4.5 miles per hour. At that rate, how far can she walk in 50 minutes?
  2. The real estate tax for a house valued at $150,000 is $1,575. At this rate, what is the value of a house for which the real estate tax is $2,299.50?
    1. Set up as a percent and solve.
    2. Set up as a proportion and solve.
  3. Michael took 2 and a half hours to drive 157.5 miles on the toll road. If he continues at that rate, how many hours will it take him to drive a distance of 210 miles?
  4. In a wildlife study, 50 penguins are captured, tagged, and then returned. A few weeks later in the same area, 300 penguins are examined. Of those 300, four penguins have tags. Estimate the number of penguins in the area.
  5. If 6 pounds of carrots yield 20 cups of trimmed, cleaned, grated carrots, how many pounds of carrots are needed to obtain 7 cups of trimmed, cleaned, grated carrots?
  6. The ratio of the weight of an object on Earth to the weight of the same object on Pluto is 100 to 3. If an elephant weighs 15,400 lbs (pounds) on Earth, how much would it weigh on Pluto?
  7. A 170 lb person weighs 85 pounds on Mars. How much would our 15,400 lb elephant weigh on Mars?
  8. There are 110 calories for 28.4 grams of Rice Crispy treat. How many calories would 42.6 grams have?
  9. A blueprint is scaled to one inch equals four feet. Find the length of a closet which is drawn as [latex]4\frac34[/latex] inches.
  10. At a certain animal shelter, the ratio of puppies to adult dogs is 7 to 4. This week there are a total of 55 dogs in the shelter. How many puppies are in the shelter this week? How many adult dogs are in the shelter this week?
  11. A team of college administrators captured and tagged a group of 90 fraternity men and then returned them to the university campus. Later a group of sorority women wishing to estimate the number of fraternity men on campus captured 245 men and found that 35 of them were tagged. How many frat men would they estimate there were on this campus?
  12. If there are 95 male students for every 100 female students at Northwest Vista College, to the nearest 0.1%, what percent of the students are female?
  13. Grills Are Us is attempting to stimulate business by offering a ”We Pay the Tax” day. Their advertisement includes the statement, ”Come buy a $400 barbecue pit without paying any sales tax!” Even though it appears that the customer pays no tax, Grills Are Us must still send a portion of the $400 to the appropriate taxing authority. Essentially, the $400 that the customer pays includes the tax. Hence, the seller must calculate the actual before-tax price of the barbecue pit, which the price for which the item could have been sold, so that after 8.25% tax is added on, the total would be $400. What is the actual selling price of the barbecue pit, so that the $400 out-the-door price includes the 8.25% tax? Round to the nearest cent.
  14. Cindi sees a bag she wants for $32.99. If the bag is on sale for 30% off, how much of a discount will she receive? What will be the sale price?
  15. Mana wants to buy a TV for $1,250, but it is on sale for 10% off. If the sales tax is 8.25%, how much tax will he have to pay? What will the total cost of the TV be?
  16. Ginger gets a haircut that costs $35. She really likes her haircut and wants to leave a 20% tip to her hairdresser. How much tip will she leave?
  17. The cost of Robert’s tickets decreased as the season went on. They started at $45 and eventually sold for $23. What was the percent decrease to the nearest percent?
  18. Explain when a proportion problem can be solved as a percent problem.

Solve.

  1. In the Mississippi River Delta, fresh water (0% salinity) mixes with salt water from the Gulf of Mexico ([latex]3\frac12\%[/latex] salinity). If 1,000 gallons of river water mixes with 3,000 gallons from the Gulf, how many gallons result, and what is its percent salinity? (Estimate a reasonable percent range for your answer before you solve.)
  2. If you add [latex]\frac12[/latex] cup of creamer (20% butterfat) to 2 cups of coffee, how many cups result and what is the
    percent butterfat of the mixture? (Estimate a reasonable percent range for your answer before you solve.)
  3. recipe for Irish coffee calls for [latex]\frac14[/latex] cup of Baileys at 12% alcohol and [latex]1\frac12[/latex] cups coffee. How much liquid is there total (in cups)? What percent alcohol is the Irish coffee? (Estimate a reasonable percent range for your answer before you solve.)
  4. Two quarts of half-and-half (10% butterfat) is mixed with some whole milk (3% fat). If there are 5 quarts of the mixture, how many quarts of whole milk were used? What is the percentage of fat in this mixture? (Estimate a reasonable percent range for your answer before you solve.)
  5. Two liters of 3% milk is mixed with some 1% low-fat milk. If there are 5 liters of the mixture, how many liters of 1% low-fat milk were used? What is the percentage of fat in this mixture? (Estimate a reasonable percent range for your answer before you solve.)

License

College Algebra for Non-STEM Majors Copyright © by Amy Collins Montalbano. All Rights Reserved.

Share This Book