Other Functions
Prep for Polynomial Functions and Their Graphs
-
-
- two
- [latex](-2,0)[/latex] and [latex](2,0)[/latex]
- cross
-
- three
- [latex](-3,0)[/latex], [latex](-1,0)[/latex], and [latex](2,0)[/latex]
- cross
-
- one
- [latex](-2,0)[/latex]
- bounces off
-
- none
- none
- neither
- [latex]x=-\frac12\;\text{and}\;x=3[/latex]
- [latex]\begin{array}{lc}x=-2&x=9\\x+2=0&x-9=0\\(x+2)(x-9)=0&{}\end{array}[/latex]
- [latex](x+3)(x-8) = 0[/latex]
- [latex]x(x-5) = 0[/latex]
- [latex](x-4)(10x+7) = 0[/latex]
- [latex](x-2)^2 = 0[/latex]
- [latex](3x-2)(2x+1) = 0[/latex]
- [latex](x+4)(5x-3) = 0[/latex]
-
Classwork: Polynomial Functions and Their Graphs
-
- 3 roots
- 4th degree
- [latex]f(x) = x(x-1)^2(x-2)[/latex]
-
- 4 roots
- 4th degree
- [latex]f(x) = (x-1)(x-2)(x-3)(x-4)[/latex]
-
- 2 roots
- 3th degree
- [latex]f(x) = x(x+2)^2[/latex]
-
- 2 roots
- 3th degree
- [latex]f(x) = (2x+1)^2(x-3)[/latex]
Homework: Polynomial Functions and Their Graphs
-
- i
- c
- m
- b
- a
- e
- l
- f
- d
- n
- j
- g
- h
- k
Prep for Rational Functions
-
- undefined
- 0
- undefined
- 0
- [latex]x = 7[/latex]
- [latex]x = -3[/latex]
- [latex]x = \frac{9}{2}[/latex]
- [latex]x = -\frac{7}{4}[/latex]
- [latex]x = -1[/latex]
- [latex]x = 1, -\frac{1}{2}[/latex]
- [latex]x = -7, \frac{3}{2}[/latex]
-
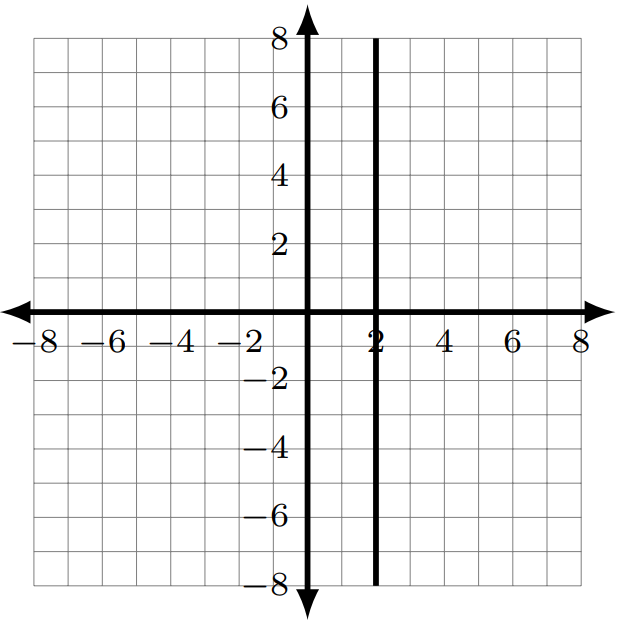
- undefined
- [latex](2,0)[/latex]
- none
-
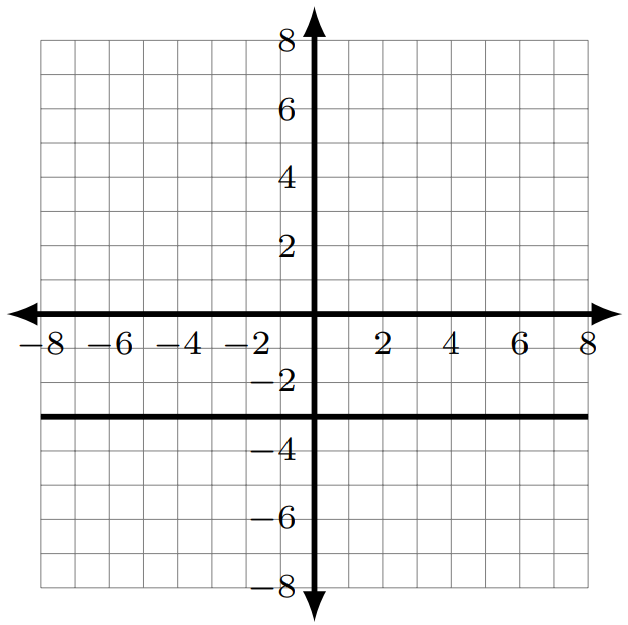
- [latex]m=0[/latex]
- none
- [latex](0,-3)[/latex]
- (a), (c), (e), (i), (j)
Classwork: Rational Functions
| x | f(x) | x | f(x) |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 0.5 | 2 | 2 | 0.5 |
| 0.25 | 4 | 4 | 0.25 |
| 0.2 | 5 | 5 | 0.2 |
| 0.125 | 8 | 8 | 0.125 |
| 0.1111 | [latex]\approx9[/latex] | 9 | [latex]\approx0.1111[/latex] |
| 0.1 | 10 | 10 | 0.1 |
- The value of y becomes larger as x becomes smaller.
- The value of y becomes smaller as x becomes larger.
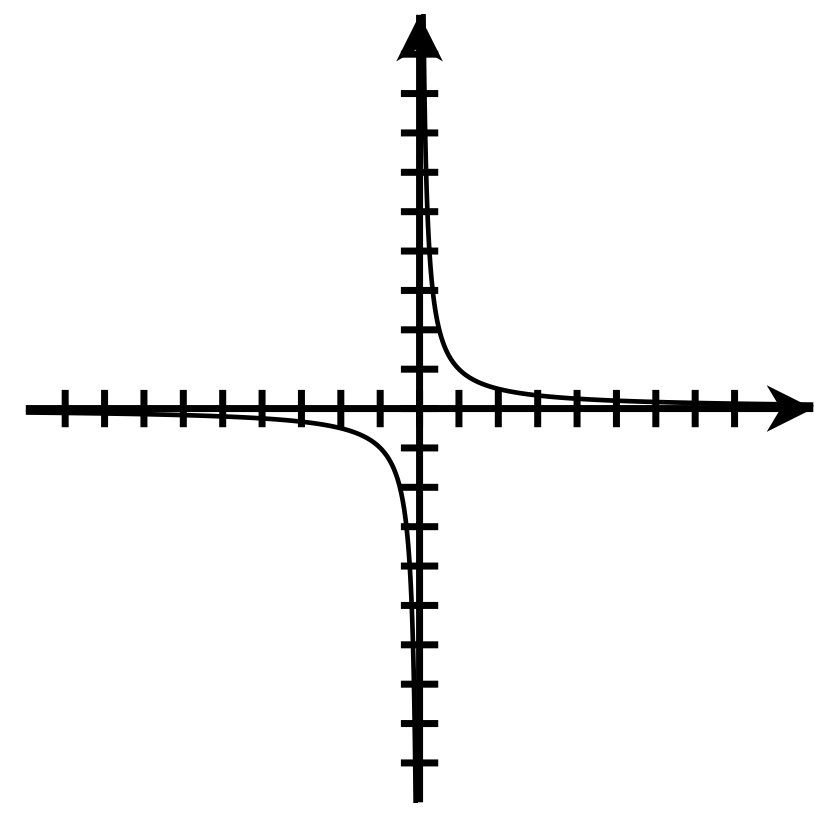
-
- [latex]VA:\;x\;=\;6;\;\text{Domain}:\;x\neq\;6\;\text{or}\;(\infty,\;6)\;\cup\;(6,\;\infty)[/latex]
- [latex]VA:\;x\;=\;-2,8;\;\text{Domain}:\;x\neq\;-2,8\;\text{or}\;(-\infty,\;-2)\;\cup\;\left(-2,8\right)\cup(8,\;\infty)[/latex]
- [latex]VA:\;x=\pm2;\;\text{Domain}:x\neq\pm2;\;\text{or}\;(-\infty,-2)\;\cup\;\left(-2,2\right)\cup(2,\;\infty)[/latex]
- [latex]VA:\;x=0,8;\;\text{Domain}:x\neq0,8\;\text{or}\;(-\infty,0)\;\cup\;\left(0,8\right)\cup(8,\;\infty)[/latex]
- Many answers possible.
- Answers may vary.
- Many answers possible.
-
- 1,800 flowers
- 90,000 flowers
- 100% removal is impossible because it requires infinitely many flowers.
-
- $2,333
- The cost of removing 2 tons of pollution would be infinite.
- The more you play, the lower your score.
- Any score less than or equal to 18
Homework: Rational Functions
-
- [latex]\begin{array}{l}\text{VA:}\,x=\frac{10}3\text{; Domain:} x\neq\frac{10}3 \text{ or} \left(-\infty,\frac{10}3\right)\cup\left(\frac{10}3,\infty\right)\end{array}[/latex]
- [latex]\begin{array}{l}\text{VA:}\,x=\pm4\text{; Domain:} x\neq\pm4 \text{ or} {(-\infty,-4)}\cup{(-4,4)}\cup{(4,\infty)}\end{array}[/latex]
- [latex]\begin{array}{l}\text{VA:}\,x=0\text{; Domain:} x\neq0 \text{ or} {(-\infty,0)}\cup{(0,\infty)}\end{array}[/latex]
- [latex]\begin{array}{l}\text{VA:}\,x=-1,5\text{; Domain:} x\neq-1,5 \text{ or} {(-\infty,-1)}\cup{(-1,5)}\cup{(5,\infty)}\end{array}[/latex]
- Answers may vary.
- Many answers are possible.
- Explain.
- Explain.
-
- [latex]t=\frac dr[/latex]
- 3 hours, 15 min
- Time approaches infinity
-
- $445,000,000
- 1,954 miles because cost would be infinite.
-
- [latex]P=\frac{n\left(8.314\right)T}V[/latex]
- When volume increases, pressure decreases.
- When volume decreases, pressure increases.
- V could not be 0 because pressure would be infinite.
-
- 6 liters
- [latex]\;325.16\;K\;\text{or}\;52.16^\circ C[/latex]
- 1329.04 in3
- [latex]35.57^\circ C[/latex]
Prep for Exponential Functions
-
- 0.65
- 0.105
- 0.0025
- 0.0875
- 0.000045
- 0.076
- -0.00035
- [latex]\begin{array}{lc}D&x^3\\F&3x\\B&\frac13x\\C&x-3\\E&x+3\\A&3^x\end{array}[/latex]
- They are not the same.
-
- 1.07%, 0.0107
- $500
- 5 years
- compounded weekly
-
- [latex]1\frac14\%\;1.25\%,\;0.0125[/latex]
- 12 months, 1 year
-
- 2.5%, 0.025
- 15 months, 1.25 years
Classwork: Exponential Functions
-
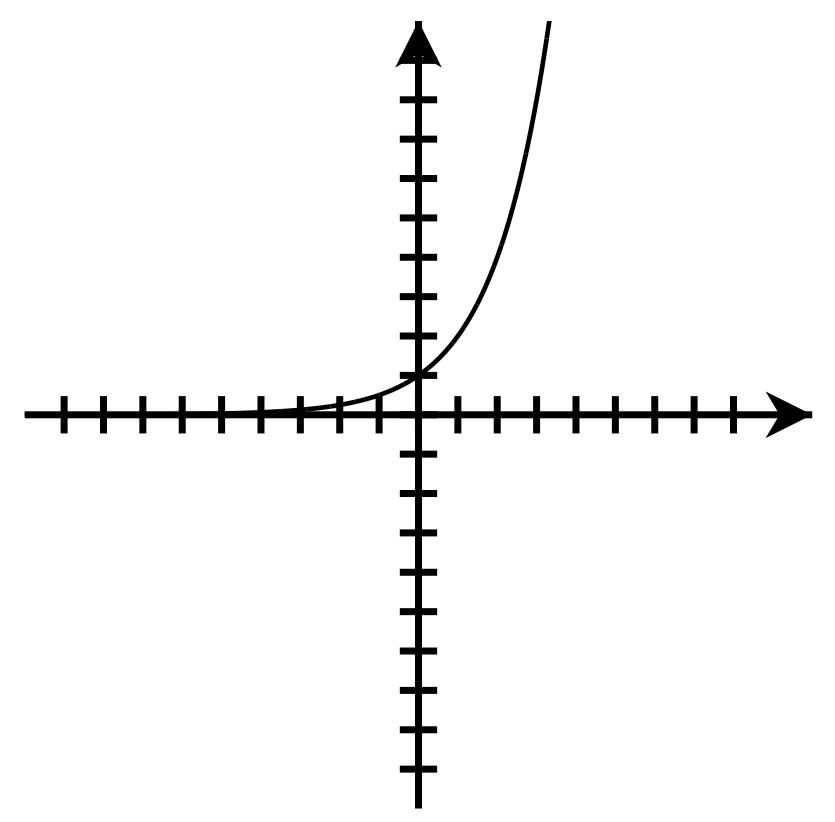 Domain: [latex]\left(-\infty,\infty\right)[/latex]
Domain: [latex]\left(-\infty,\infty\right)[/latex]
Range: [latex]\left(0,\infty\right)[/latex]
y-intercept: [latex](0,1)[/latex]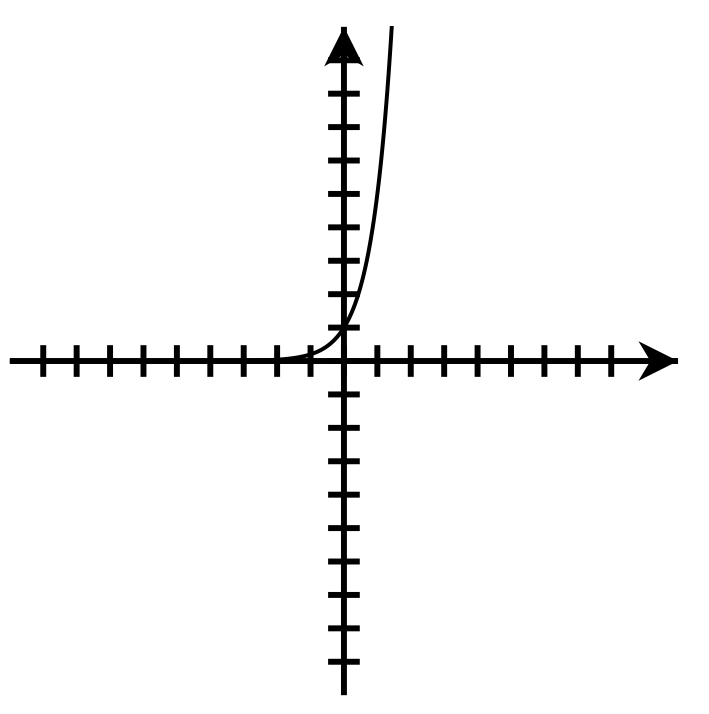 Domain: [latex]\left(-\infty,\infty\right)[/latex]
Domain: [latex]\left(-\infty,\infty\right)[/latex]
Range: [latex]\left(0,\infty\right)[/latex]
y-intercept: [latex](0,1)[/latex]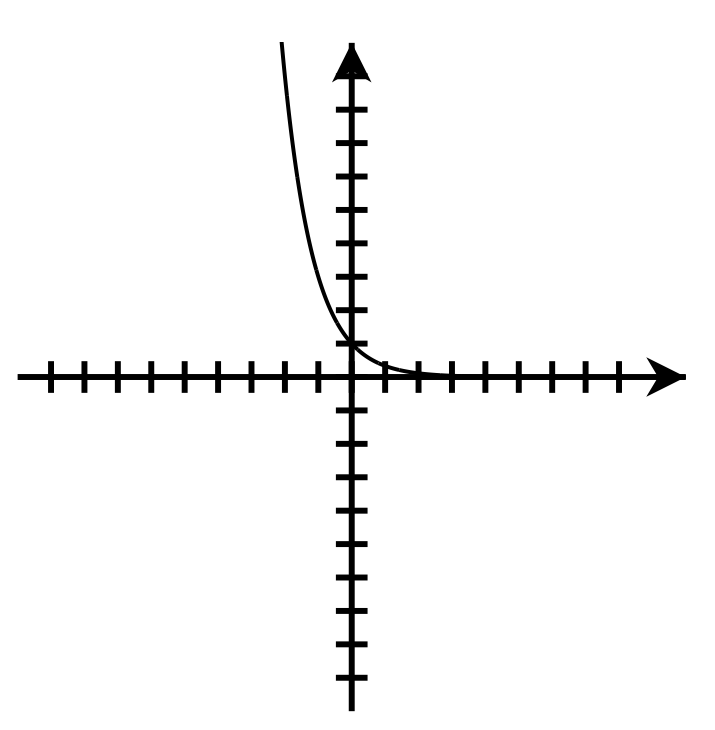 Domain: [latex]\left(-\infty,\infty\right)[/latex]
Domain: [latex]\left(-\infty,\infty\right)[/latex]
Range: [latex]\left(0,\infty\right)[/latex]
y-intercept: [latex](0,1)[/latex]
-
- [latex]$130[/latex]
- [latex]$134.59[/latex]
- [latex]$134.95[/latex]
- [latex]$134.98[/latex]
- [latex]$134.99[/latex]
-
- [latex]$900.00[/latex]
- [latex]$905.13[/latex]
- [latex]$906.40[/latex]
- [latex]$906.49[/latex]
- [latex]$906.52[/latex]
- [latex]$906.52[/latex]
-
- 25,000 bacteria
- 83,003 bacteria
- [latex]$12,754.31[/latex]
- [latex]$44,260.17[/latex]
- [latex]$227,726.54[/latex]
- Bank B
-
- 0.972 kg
- 0.752 kg
-
- 10 mg
- 8.41 mg at 1 hour; 5.01 mg at 4 hours
Homework: Exponential Functions
-
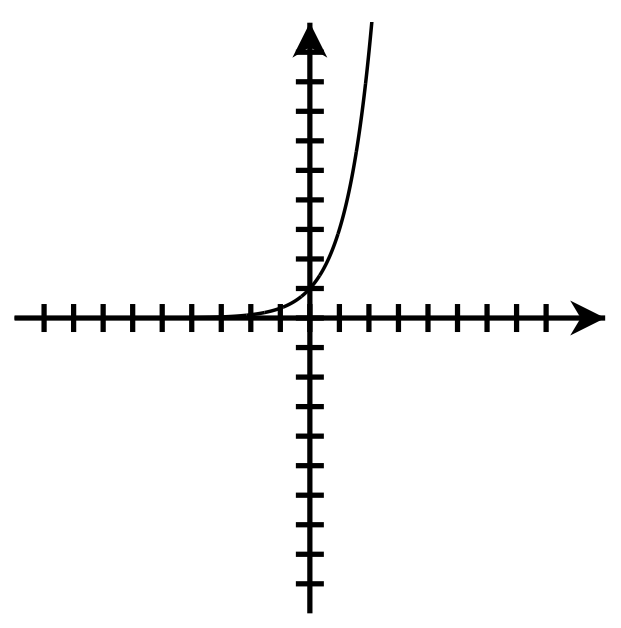 Domain: [latex]\left(-\infty,\infty\right)[/latex]
Domain: [latex]\left(-\infty,\infty\right)[/latex]
Range: [latex]\left(0,\infty\right)[/latex]
y-intercept: [latex](0,1)[/latex]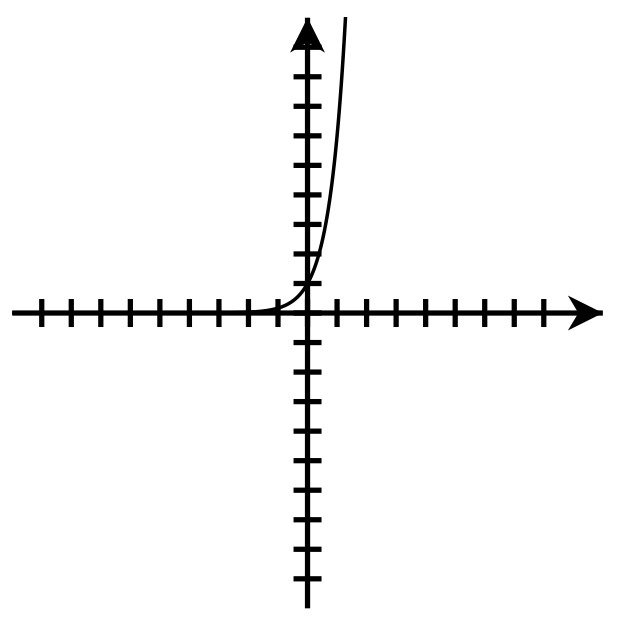 Domain: [latex]\left(-\infty,\infty\right)[/latex]
Domain: [latex]\left(-\infty,\infty\right)[/latex]
Range: [latex]\left(0,\infty\right)[/latex]
y-intercept: [latex](0,1)[/latex]- Explain.
- Explain.
- [latex]$9,449.01[/latex]
- [latex]$2,139.05[/latex]
- [latex]$2,208.04[/latex]
- [latex]$18,505.17[/latex]
- [latex]$618,990.79[/latex]
- The second loan
- [latex]9.42\times10^{-12}[/latex] thousand TBq
- 0 TBq
- Answer will vary each year
- 3.35 mg at 1 hour; 0.45 mg at 6 hours
Prep for Inverse Functions
-
x y = 2x -2 -4 -1 -2 0 0 1 2 2 4 3 6 -
x [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol y}{\color[rgb]{1.0, 1.0, 1.0}\mathbf=}{\color[rgb]{1.0, 1.0, 1.0}\frac{\mathbf x}{\mathbf2}}[/latex] -4 -2 -2 -1 0 0 2 1 4 2 6 3 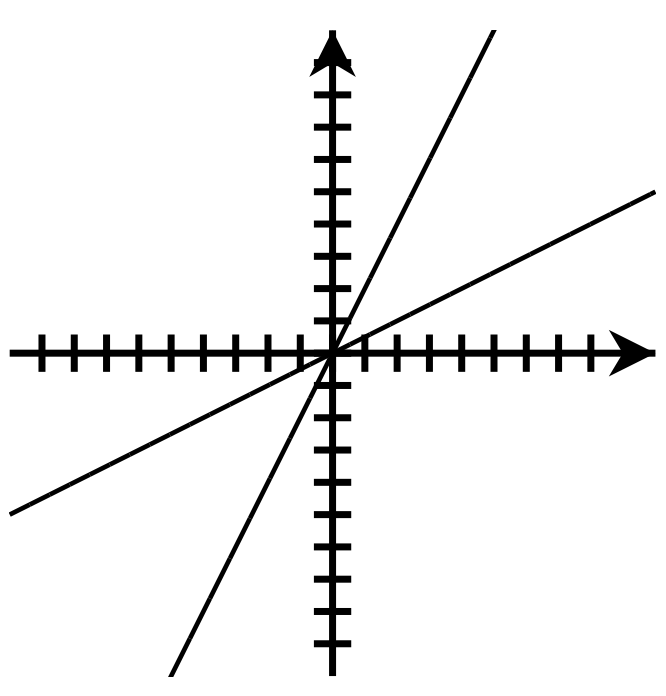
- The x-and y-coordinates are switched.
- [latex]x[/latex]
- [latex]x[/latex]
- [latex]x[/latex]
- [latex]x[/latex]
- [latex]4[/latex]
- [latex]6[/latex]
- [latex]2[/latex]
- [latex]8[/latex]
- [latex]0.45[/latex]
- [latex]0.1825[/latex]
- [latex]0.0015[/latex]
- [latex]0.129[/latex]
- [latex]0.00005[/latex]
- [latex]-0.022[/latex]
- [latex]-0.00269[/latex]
-
- [latex]$7,000[/latex]
- [latex]8.5\%, 0.085[/latex]
- [latex]$10,000[/latex]
- time
-
- The balance is [latex]$14,000[/latex] instead of [latex]$10,000[/latex]
- time
-
- [latex]$1,000[/latex]
- [latex]$1,245[/latex]
- interest rate
Classwork: Inverse Functions
-
x [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol y}{\color[rgb]{1.0, 1.0, 1.0}\mathbf=}{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}^{\color[rgb]{1.0, 1.0, 1.0}\mathbf2}[/latex] 0 0 [latex]\frac{1}{3}[/latex] [latex]\frac{1}{9}[/latex] [latex]\frac{1}{2}[/latex] [latex]\frac{1}{4}[/latex] 1 1 2 4 3 9 -
x [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol y}{\color[rgb]{1.0, 1.0, 1.0}\mathbf=}{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}^{\color[rgb]{1.0, 1.0, 1.0}\frac{\mathbf1}{\mathbf2}}[/latex] 0 0 [latex]\frac{1}{9}[/latex] [latex]\frac{1}{3}[/latex] [latex]\frac{1}{4}[/latex] [latex]\frac{1}{2}[/latex] 1 1 4 2 9 3 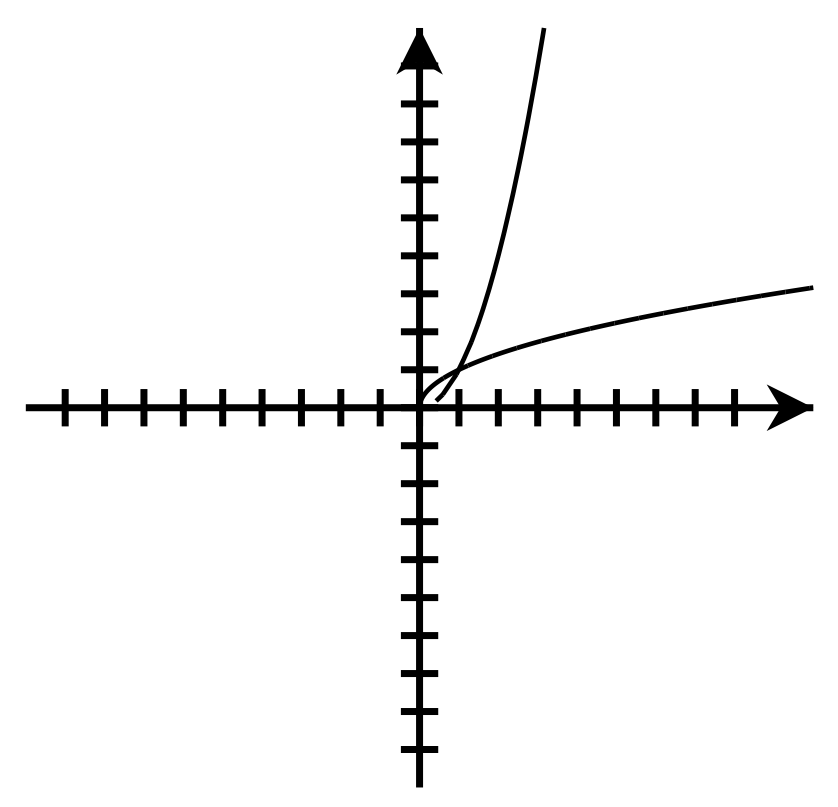
- The x- and y-coordinates are switched.
- [latex]x=9[/latex]
- [latex]x=3[/latex]
Classwork: Inverse Functions — In (x) and ex
-
x [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol y}{\color[rgb]{1.0, 1.0, 1.0}\mathbf=}{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol e}^{\color[rgb]{1.0, 1.0, 1.0}\mathbf x}[/latex] -3 0.05 -2 0.14 -1 0.37 0 1 1 2.72 2 7.39 -
x [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol y}{\color[rgb]{1.0, 1.0, 1.0}\mathbf=}{\color[rgb]{1.0, 1.0, 1.0}\mathbf ln}\mathbf{\color[rgb]{1.0, 1.0, 1.0}\left(x\right)}[/latex] 0.05 -3 0.14 -2 0.37 -1 1 0 2.72 1 7.39 2 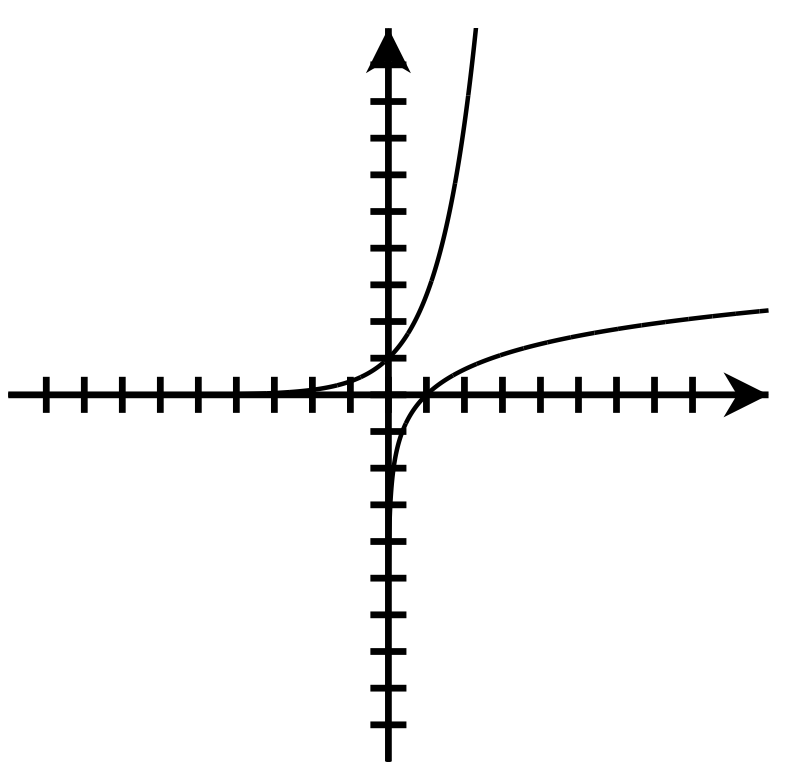
- The x- and y- coordinates are switched.
[latex]y=e^x[/latex], Domain: [latex]\left(-\infty,\infty\right)[/latex] Range: [latex]\left(0,\infty\right)[/latex]
y = ln(x), Domain: [latex]\left(0,\infty\right)[/latex] Range: [latex]\left(-\infty,\infty\right)[/latex].
- 0
- [latex]\approx2.08[/latex]
- [latex]\approx6.68[/latex]
- [latex]\approx8.99[/latex]
- Explain in your own words.
- 3
- 13
- 7
- 5
- 8
- 15
- [latex]k = \frac{\ln(8)}{10}[/latex]
- [latex]x = \frac{1}{2}[/latex]
- [latex]x = e + 2[/latex]
- [latex]x = 3[/latex]
- [latex]P = \frac{50}{e^{0.6}}[/latex]
- [latex]k = \frac{\ln(\frac{1}{2})}{7}[/latex]
- [latex]t = 23.1 \text{ years}[/latex]
- [latex]10.62\% \text{ per year}[/latex]
- [latex]P = \$2,137.07[/latex]
Homework: Inverse Functions — ln(x) and ex
-
- [latex]x = \frac{\ln(12)}{3}[/latex]
- [latex]x = \ln(72)[/latex]
- [latex]t = \frac{\ln(5)}{.06}[/latex]
- [latex]t=-\frac{\ln\left(\frac12\right)}{.0000124}[/latex]
- [latex]r = \frac{\ln(\frac{1}{2})}{15}[/latex]
- [latex]x = e^{3.548}[/latex]
- [latex]x = \frac{e^5 - 1}{3}[/latex]
- [latex]x = \frac{e + 7}{4}[/latex]
- [latex]r = \frac{13}{150}[/latex]
- [latex]I = 24[/latex]
- The [latex]+20[/latex] must be undone first;
Correct answer: [latex]e^{15}[/latex] - [latex]e[/latex] should be used as the base of both sides;
Correct answer: [latex]\frac{1}{50}[/latex]
- 4.2 years (or)
4 years, 2 months, and 12 days - 8.15 years
-
- 11.55 years
- 18.31 years
Classwork: Inverse Functions — log(x) and 10x
-
x [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol y}{\color[rgb]{1.0, 1.0, 1.0}\mathbf=}{\color[rgb]{1.0, 1.0, 1.0}\mathbf10}^{\color[rgb]{1.0, 1.0, 1.0}\mathbf x}[/latex] -3 0.001 -2 0.01 -1 0.1 0 1 1 10 2 100 -
x y 0.001 -3 0.01 -2 0.1 -1 1 0 10 1 100 2 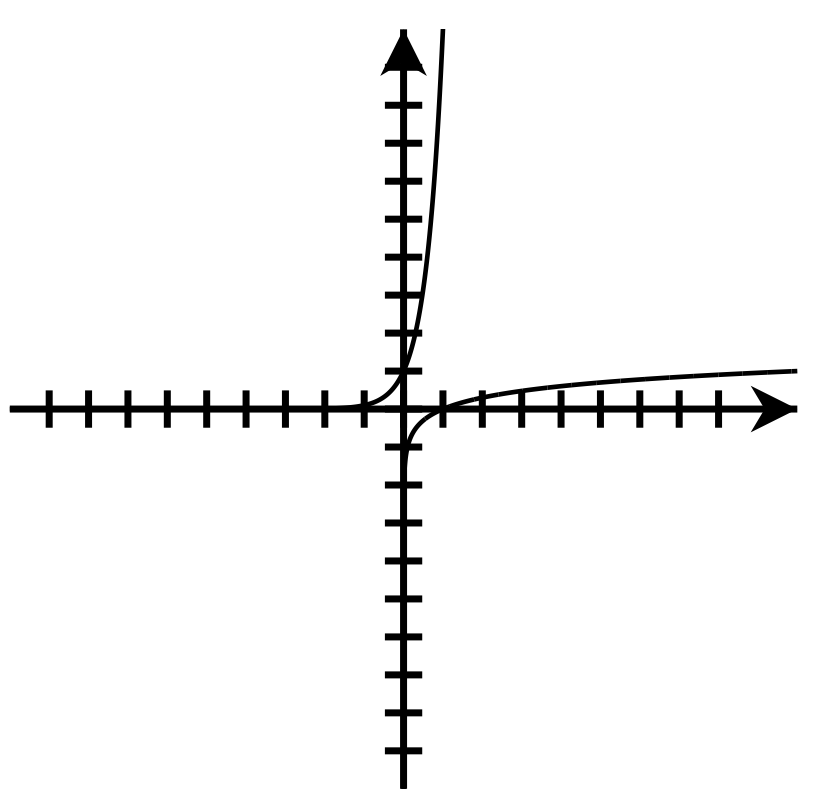
- The x- and y- coordinates are switched.[latex]y=10^x[/latex], D: [latex]\left(-\infty,\infty\right)[/latex] R: [latex]\left(0,\infty\right)[/latex]
[latex]y=\log\left(x\right)[/latex], D: [latex]\left(0,\infty\right)[/latex] R: [latex]\left(-\infty,\infty\right)[/latex].
- 0
- [latex]\approx0.903[/latex]
- [latex]\approx2.903[/latex]
- [latex]4[/latex]
- Explain in your own words.
- 5
- 9
- 7
- 2
- 5
- [latex]x = \log(400)[/latex]
- [latex]x = 3[/latex]
- [latex]x = \frac{1}{2}[/latex]
- [latex]x = 12[/latex]
- [latex]x = \log(12)[/latex]
- [latex]x = 10^{-7}$ or $0.0000001[/latex]
- Answers will vary.
- [latex]k=-1.93%[/latex] per hour
- [latex]\approx3.04\;\mathrm{pH}[/latex]
- [latex]3.16\times10^{-12}\;\mathrm{mol}/\mathrm L[/latex]
- [latex]\approx2.4\;\mathrm{pH}[/latex]
- No, both have a [latex]\mathrm{pH}5[/latex]
- [latex]\approx\;7.38[/latex] magnitude
- [latex]1.26\times10^6\;\mathrm{mm}[/latex]
Homework: Inverse Functions — log(x) and 10x
- [latex]x = \log(30)[/latex]
- [latex]x = 2[/latex]
- [latex]x = \log(3)[/latex]
- [latex]x = 102[/latex]
- [latex]x = \frac{1}{3}[/latex]
- [latex]P \approx \$3,785.74[/latex]
- [latex]x = \frac{\log(20)}{0.05}[/latex]
- [latex]x=\frac{\log\left(\frac32\right)}3[/latex]
-
- 1.37% per year
- 1.75 million people
- [latex]\approx29.5[/latex] years after 2010, or sometime in 2039
- 6 days
- 34.66% per min
- -0.04% per year; the sign is negative because the function models decay
- 2 hours
- [latex]4.0\times10^{-8}\;\mathrm{mol}/\mathrm L[/latex]
- [latex]4.7\;\mathrm{pH}[/latex]
- [latex]3.16\times10^{-4}\;\mathrm{mol}/\mathrm L[/latex]
- [latex]12.4\;\mathrm{pH}[/latex]
- 7.09 magnitude
- 63.1 mm
- 630.96 mm
- 100 times stronger
- 6.699 magnitude; 10.699 magnitude; every power of 10 increase/decrease in seismographic reading results in a corresponding 1 point increase/decrease in Richter scale reading.
Classwork: Solving Other Exponential and Logarithmic Equations
-
- [latex]x = 9[/latex]
- [latex]x = -2[/latex]
- [latex]x = 218[/latex]
- [latex]x = \sqrt{7} + 2[/latex]
- [latex]x = -\frac{11}{4}[/latex]
- [latex]x = 38[/latex]
- Take ln of both sides.
- Make both sides exponents of base 10.
- Make both sides exponents of base 3.
- [latex]3 \ln x[/latex]
- [latex]5 \log(x-2)[/latex]
- [latex]-\frac{1}{2} \log_5 x[/latex]
- [latex]\frac{2}{5} \ln x[/latex]
- [latex]c \ln b[/latex]
- 9.551
- 22.925
- 69.661
- 0.28125
- 40
- 2.46875
- [latex]x = -\frac{11}{2}[/latex]
- [latex]x = 3[/latex]
- [latex]x = 3[/latex]
- [latex]x = 4[/latex]
- [latex]x = 2[/latex]
- [latex]x = \frac{3}{5}[/latex]
- [latex]x = -2[/latex]
- [latex]x = -\frac{3}{2}[/latex]
Homework: Solving Other Exponential and Logarithmic Equations
-
- [latex]x=\log(34,926)[/latex]
- [latex]x=\ln(64)[/latex]
- [latex]x = 2,187[/latex]
- [latex]x=\log_4(1024)=5[/latex]
- [latex]x=\frac{e^3}5[/latex]
- [latex]x=\frac{\ln(11250)+5}4[/latex]
- [latex]x=\frac{\ln(7957)-1}{-8}[/latex]
- [latex]x=\frac{\ln\left(\frac{10273}4\right)}7[/latex]
- [latex]x = \frac{3}{2}[/latex]
- [latex]x = 5[/latex]
- [latex]x = 4[/latex]
- [latex]t=\frac{\ln(5)}{0.06}[/latex]
- [latex]k=\frac{\ln\left(\frac12\right)}7[/latex]
- [latex]k=\frac{\ln\left(\frac12\right)}{10,000}[/latex]
- [latex]t = \frac{\ln(2)}{\ln(1.01)}[/latex]
- [latex]x = 25[/latex]
- [latex]x = \frac{2}{3}[/latex]
- [latex]x = \frac{\log_4(6)}{3}[/latex]
- [latex]x = 47.5[/latex]
- [latex]x = 200[/latex]
- 4% per year
- 3.4 years
-
- 3,351 pop
- 4,492 pop
- 5,679 pop
- [latex]P\;=\;240,\;360e^{.012t}[/latex]; 11.22 years from 2000
- 158.64% per min
-
- 0.028 per year (decay)
- 2,485 years
- 4% per year
- 3.75% per year
- $8,824.97
- FYAB is better
-
- 7.5 min
- 66.17 bmp

