"

1.4: Library of functions; piecewise-defined functions

Learning Objectives

  1. Identify parent functions.
  2. Find the domain of a function.
  3. Evaluate a piecewise-defined function.
  4. Graph a piecewise-defined function.

Identify parent functions and its domain

Function Graphs Properties
Constant Function

[latex]f\left(x\right)=c[/latex]

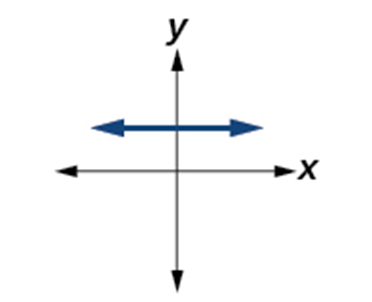 Graph of a function described in the left column. Even Function

Neither increasing nor decreasing, constant function.

Domain: [latex]\left(-\infty,\;\infty\right)[/latex]
Identity Function

[latex]f\left(x\right)=x[/latex]

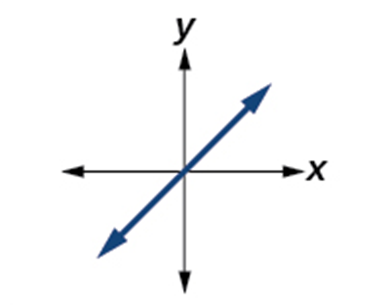 Graph of a function described in the left column. Odd Function.

Increasing function.

Domain: [latex]\left(-\infty,\;\infty\right)[/latex]
Quadratic Function

[latex]f\left(x\right)=x^2[/latex]

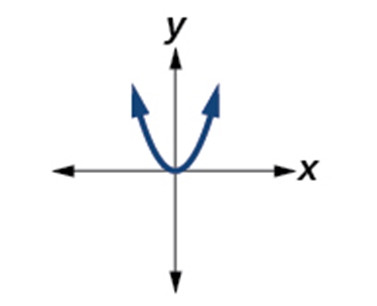 Graph of a function described in the left column. Even Function

Increasing on [latex]\left(0,\;\infty\right)[/latex]

Decreasing on [latex]\left(-\infty,\;0\right)[/latex]

Minimum at [latex]x=0[/latex]

Domain: [latex]\left(-\infty,\;\infty\right)[/latex]
Cubic Function

[latex]f\left(x\right)=x^3[/latex]

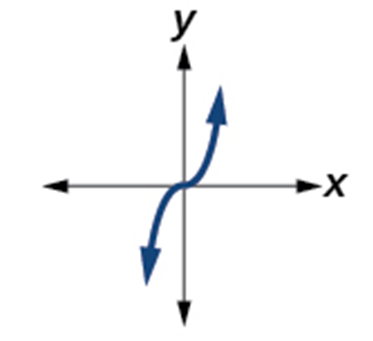 Graph of a function described in the left column. Odd Function.

Increasing function.

Domain: [latex]\left(-\infty,\;\infty\right)[/latex]
Reciprocal Function

[latex]f\left(x\right)=\frac1x[/latex]

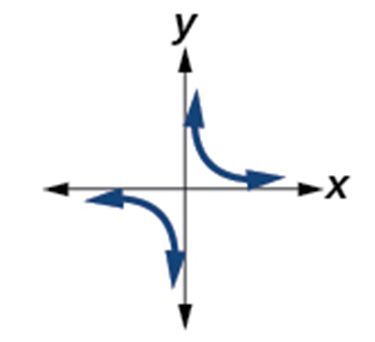 Graph of a function described in the left column. Odd Function.

Decreasing on [latex]\left(-\infty,\;0\right)\cup\left(0,\;\infty\right)[/latex]

Domain: [latex]\left(-\infty,\;0\right)\cup\left(0,\;\infty\right)[/latex]
Reciprocal Squared

[latex]f\left(x\right)=\frac1{x^2}[/latex]

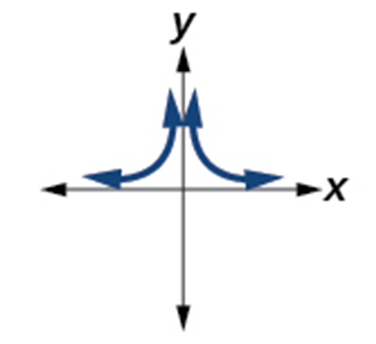 Graph of a function described in the left column. Even Function

Increasing on [latex]\left(-\infty,\;0\right)[/latex]

Decreasing on [latex]\left(0,\;\infty\right)[/latex]

Domain: [latex]\left(-\infty,\;0\right)\cup\left(0,\;\infty\right)[/latex]
Cube Root

[latex]f\left(x\right)=\sqrt[3]x[/latex]

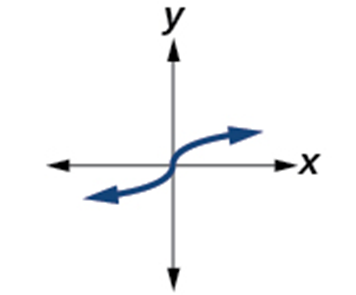 Graph of a function described in the left column. Odd Function.

Increasing function.

Domain: [latex]\left(-\infty,\;\infty\right)[/latex]
Square Root

[latex]f\left(x\right)=\sqrt x[/latex]

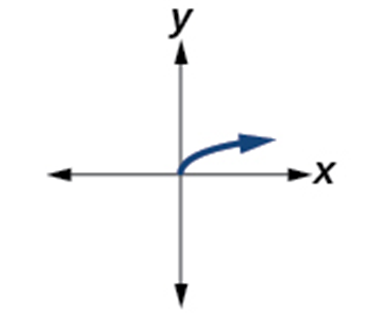 Graph of a function described in the left column. Increasing on [latex]\left(0,\;\infty\right)[/latex]

Domain: [latex]\lbrack0,\;\infty)[/latex]

It is neither. (not even, not odd)
Absolute Value

[latex]f\left(x\right)=\left|x\right|[/latex]

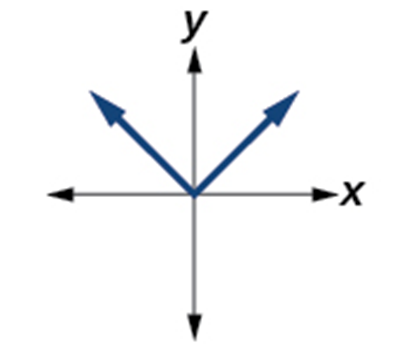 Graph of a function described in the left column. Even Function

Increasing on [latex]\left(0,\;\infty\right)[/latex]

Decreasing on [latex]\left(-\infty,\;0\right)[/latex]

Domain: [latex]\left(-\infty,\;\infty\right)[/latex]

Piecewise-defined function

Definition: A piecewise function is a function in which more than one formula is used to define the output over different pieces of the domain.

It is a function in which more than one formula is used to define the output. Each formula has its own domain, and the domain of the function is the union of all these smaller domains. We notate this idea like this:

[latex]f\left(x\right)=\left\{\begin{array}{lc}formula\;1&if\;x\;is\;in\;domain\;1\\formula\;2&if\;x\;is\;in\;domain\;2\\formula\;3&if\;x\;is\;in\;domain\;3\end{array}\right.[/latex]

In piecewise notation, the absolute value function is

[latex]\left|x\right|=\left\{\begin{array}{lc}x&if\;x\;\geq\;0\\-x&if\;x\;<\;0\end{array}\right.[/latex]

How to evaluate a piecewise-defined function

Given a piecewise function, write the formula and identify the domain for each interval.

  1. Identify the intervals for which different rules apply.
  2. Determine formulas that describe how to calculate an output from an input in each interval.
  3. Use braces and if-statements to write the function.

Example 1.4-3-1: Evaluate the piecewise function.

fx=–x+2ifx<34if4<x<5x+3ifx≥7

[latex]f\left(4\right)=[/latex] _____________

[latex]f\left(9\right)=[/latex] _____________

[latex]f\left(0\right)=[/latex] _____________

Master L3 Key

Example 1.4-3-1: Evaluate the piecewise function.

fx=–x+2ifx<34if4<x<5x+3ifx≥7

[latex]f\left(4\right)=NA[/latex]

The domain of the given function does not include [latex]x=4[/latex]; therefore, we cannot identify the value of [latex]f(x)[/latex] at that point.

Character
You might wonder why we don’t use the function [latex]f(x)=4[/latex]. The reason is that the domain does not include [latex]x\geq4[/latex], so we cannot use this function to evaluate [latex]f(4)[/latex].

[latex]f\left(9\right)=6[/latex]

[latex]f(9)[/latex] means finding the y-value when [latex]x =9[/latex]. Based on the given function, we will use the third piece of the function [latex]f\left(x\right)=\sqrt x+3[/latex] if [latex]x\geq7[/latex] (since [latex]9>7[/latex]).

Substitute 9 for [latex]x[/latex].

[latex]f\left(x\right)=\sqrt x+3[/latex]

[latex]f\left(9\right)=\sqrt9+3[/latex]

[latex]f\left(9\right)=3+3[/latex]

[latex]f\left(9\right)=6[/latex]

[latex]f\left(0\right)=2[/latex]

[latex]f(0)[/latex] means finding the y-value when [latex]x=0[/latex]. Based on the given function, we will use the first piece of the function [latex]f\left(x\right)=-x+2[/latex] if [latex]x<3\left(0<3\right)[/latex]

Substitute 0 for [latex]x[/latex].

[latex]f\left(x\right)=-x+2[/latex]

[latex]f\left(0\right)=-0+2[/latex]

[latex]f\left(0\right)=2[/latex]

IXL | Graph points on a coordinate plane | 5th grade math Your Turn

Practice 1.4-3-1

Practice 1.4-3-2

Graph a piecewise-defined function

Given a piecewise function, sketch a graph.

  1. Indicate on the x-axis the boundaries defined by the intervals on each piece of the domain.
  2. For each piece of the domain, graph on that interval using the corresponding equation pertaining to that piece. Do not graph two functions over one interval because it would violate the criteria of a function.

Example 1.4-4-1: Graphing a Piecewise Function. Sketch a graph of the function.

fx=x2ifx≤13if1<x≤2xifx>2 

Master L3 Key

Example 1.4-4-1: Graphing a Piecewise Function. Sketch a graph of the function.

fx=x2ifx≤13if1<x≤2xifx>2

Each of the component functions is from our library of toolkit functions, so we know their shapes. We can imagine graphing each function and then limiting the graph to the indicated domain. At the endpoints of the domain, we draw open circles to indicate where the endpoint is not included because of a less-than or greater-than inequality; we draw a closed circle where the endpoint is included because of a less-than-or-equal-to or greater-than-or-equal-to inequality.

Figure shows the three components of the piecewise function graphed on separate coordinate systems.

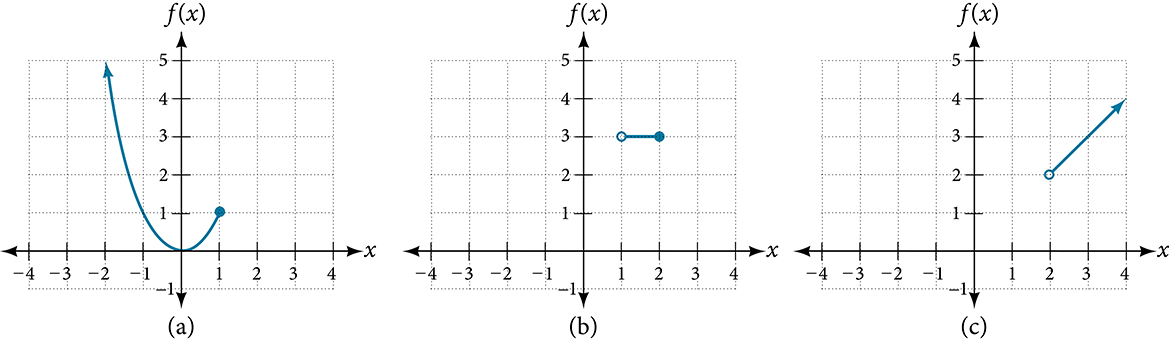
Three graphs, labeled (a), (b), and (c), are displayed on separate Cartesian coordinate systems. Each graph represents a different function, f(x), plotted against the x-axis. All three coordinate systems have x-axes ranging from -4 to 4 and y-axes ranging from -1 to 5, with grid lines at integer values. Graph (a) shows a parabola opening upwards, with its vertex at (0, 0). The curve extends upwards with an arrow indicating it continues indefinitely. There is a solid circle at the point (1, 1), indicating that this point is included in the graph. Graph (b) shows a piecewise function. There is an open circle at (1, 3), indicating that this point is not included. A horizontal line extends from this open circle to a solid circle at (2, 3), indicating that this point is included. Graph (c) shows a line segment starting with an open circle at (2, 2), indicating that this point is not included. The line segment extends diagonally upwards to the right, ending with an arrow at approximately (4, 4), indicating that the line continues indefinitely in that direction."

  1. [latex]f\left(x\right)=x^2\;if\;x\leq1;[/latex]
  2. [latex]f\left(x\right)=3\;if\;1< x\leq2;[/latex]
  3. [latex]f\left(x\right)=x\;if\;x>2[/latex]

Now that we have sketched each piece individually, we combine them in the same coordinate plane. See

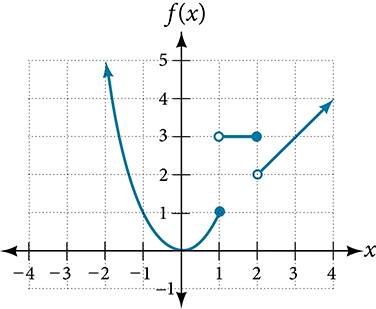
A graph of a piecewise function, labeled f(x), is shown on a Cartesian coordinate system. The x-axis ranges from -4 to 4, and the y-axis ranges from -1 to 5, with grid lines at integer values. The graph consists of three distinct parts: 1. A parabola opening upwards, with its vertex at (0, 0). This part of the graph extends from x values less than or equal to 1. It has an arrow pointing upwards for x < -2, indicating it continues indefinitely. It includes a solid circle at the point (1, 1), meaning this point is part of the function. 2. A horizontal line segment at y = 3, with an open circle at (1, 3) indicating that x = 1 is not included for this segment, and a solid circle at (2, 3), indicating that x = 2 is included. This segment represents the function for 1 < x ≤ 2. 3. A ray starting with an open circle at (2, 2), indicating that x = 2 is not included for this ray. The ray extends diagonally upwards to the right, passing through (4, 4) and continuing indefinitely as shown by an arrow. This represents the function for x > 2.

Dr LinearAnalysis

Note that the graph does pass the vertical line test even at [latex]x=1[/latex] and [latex]x=2[/latex] because the points [latex](1, 3)[/latex] and [latex](2, 2)[/latex] are not part of the graph of the function, though [latex](1, 1)[/latex] and [latex](2, 3)[/latex] are.

IXL | Graph points on a coordinate plane | 5th grade math Your Turn

Practice 1.4-4-1

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Math Mastery Manual Copyright © by Linglin (Niki) Liu is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book