"

2.4: The Real Zeros of a Polynomial Function

Learning Objectives

  1. Evaluate a polynomial using the Remainder Theorem.
  2. Find the potential zeros of a polynomial.
  3. Use the Rational Zero Theorem to find rational zeros.
  4. Use of synthetic division to divide polynomials.
  5. Find zeros of a polynomial function.

Evaluate a polynomial using the Remainder Theorem

Polynomials using the Remainder Theorem. If the polynomial is divided by [latex]x–k[/latex], the remainder may be found quickly by evaluating the polynomial function at [latex]k[/latex], that is, [latex]f\left(k\right)[/latex]. Let’s walk through the proof of the theorem.

Recall that the Division Algorithm states that, given a polynomial dividend [latex]f\left(x\right)[/latex] and a non-zero polynomial divisor [latex]d\left(x\right)[/latex], there exist unique polynomials [latex]q\left(x\right)[/latex] and [latex]r\left(x\right)[/latex] such that

[latex]f\left(x\right)=d\left(x\right)q\left(x\right)+r\left(x\right)[/latex]

and either [latex]r\left(x\right)=0[/latex] or the degree of [latex]r\left(x\right)[/latex] is less than the degree of [latex]d\left(x\right)[/latex]. In practice divisors, [latex]d\left(x\right)[/latex] will have degrees less than or equal to the degree of [latex]f\left(x\right)[/latex]. If the divisor, [latex]d\left(x\right)[/latex], is [latex]x−k[/latex], this takes the form

[latex]f\left(x\right)=\left(x-k\right)q\left(x\right)+r[/latex]

Since the divisor [latex]x−k[/latex] is linear, the remainder will be a constant, [latex]r[/latex]. And, if we evaluate this for [latex]x=k[/latex], we have

[latex]f\left(k\right)=\left(k-k\right)q\left(k\right)+r[/latex]

[latex]=0\cdot q\left(k\right)+r[/latex]

[latex]=r[/latex]

In other words, [latex]f\left(k\right)[/latex] is the remainder obtained by dividing [latex]f\left(x\right)[/latex] by [latex]x−k[/latex].

The Remainder Theorem

If a polynomial [latex]f\left(x\right)[/latex] is divided by [latex]x−k[/latex], then the remainder is the value [latex]f\left(k\right)[/latex].

How To

Given a polynomial function [latex]f[/latex], evaluate [latex]f\left(x\right)[/latex] at [latex]x=k[/latex] using the Remainder Theorem.

  1. Use synthetic division to divide the polynomial by [latex]x−k[/latex].
  2. The remainder is the value [latex]f\left(k\right)[/latex].

Example 2.4-1-1: Using the Remainder Theorem to Evaluate a Polynomial

Use the Remainder Theorem to evaluate [latex]f\left(x\right)=6x^4-x^3-15x^2+2x-7[/latex] at [latex]x=2[/latex].

Master L3 Key

Example 2.4-1-1: Using the Remainder Theorem to Evaluate a Polynomial

Use the Remainder Theorem to evaluate [latex]f\left(x\right)=6x^4-x^3-15x^2+2x-7[/latex] at [latex]x=2[/latex].

We can check our answer by evaluating [latex]f\left(2\right)[/latex].

[latex]f\left(x\right)=6x^4-x^3-15x^2+2x-7[/latex]

[latex]f\left(2\right)=6\left(2\right)^4-\left(2\right)^3-15\left(2\right)^2+2\left(2\right)-7[/latex]

[latex]=25[/latex]

Your Turn

Practice 2.4-1-1

Find the potential zeros of a polynomial

The Rational Zero Theorem

The Rational Zero Theorem states that, if the polynomial [latex]f\left(x\right)=a_nx^n+a_{n-1}x^{n-1}+\dots+a_1x+a_0[/latex] has integer coefficients [latex]a_n\neq0[/latex], then every rational zero of [latex]f\left(x\right)[/latex] has the form [latex]\frac pq[/latex] where [latex]p[/latex] is a factor of the constant term [latex]a_0[/latex] and [latex]q[/latex] is a factor of the leading coefficient [latex]a_n[/latex].

When the leading coefficient is [latex]1[/latex], the possible rational zeros are the factors of the constant term.

How To

Given a polynomial function [latex]f\left(x\right)[/latex], use the Rational Zero Theorem to find rational zeros.

  1. Determine all factors of the constant term and all factors of the leading coefficient.
  2. Determine all possible values of [latex]\frac pq[/latex], where [latex]p[/latex] is a factor of the constant term and [latex]q[/latex] is a factor of the leading coefficient. Be sure to include both positive and negative candidates.
  3. Determine which possible zeros are actual zeros by evaluating each case of [latex]f\left(\frac pq\right)[/latex]

Example 2.4-2-1: Listing All Possible Rational Zeros

List all possible rational zeros of [latex]f\left(x\right)=2x^4-5x^3+x^2-4[/latex].

Master L3 Key

Example 2.4-2-1: Listing All Possible Rational Zeros

List all possible rational zeros of [latex]f\left(x\right)=2x^4-5x^3+x^2-4[/latex].

The only possible rational zeros of [latex]f\left(x\right)[/latex] are the quotients of the factors of the last term, [latex]–4[/latex], and the factors of the leading coefficient, [latex]2[/latex].

The constant term is [latex]–4[/latex]; the factors of [latex]–4[/latex] are [latex]p=\pm1,\;\pm2,\;\pm4[/latex].

The leading coefficient is [latex]2[/latex]; the factors of [latex]2[/latex] are [latex]q=\pm1,\;\pm2[/latex].

If any of the four real zeros are rational zeros, then they will be of one of the following factors of [latex]–4[/latex] divided by one of the factors of [latex]2[/latex].

[latex]\frac pq=\pm\frac11,\;\pm\frac12[/latex]

[latex]\frac pq=\pm\frac21,\;\pm\frac22[/latex]

[latex]\frac pq=\pm\frac41,\;\pm\frac42[/latex]

Note that [latex]\frac22=1[/latex] and [latex]\frac42=2[/latex], which have already been listed. So we can shorten our list.

[latex]\frac pq=\frac{Factors\;of\;the\;last}{Factors\;of\;the\;first}=\pm1,\;\pm2,\;\pm4,\;\pm\frac12[/latex]

The image displays the detailed steps of polynomial long division. We are dividing the polynomial, which is two x cubed minus three x squared plus four x plus five, by the binomial, which is x plus two. The process starts with two x cubed divided by x, giving two x squared, which is then multiplied by the divisor, x plus two, to get two x cubed plus four x squared. This result is subtracted from the initial terms of the dividend, leaving minus seven x squared plus four x. Next, minus seven x squared is divided by x, resulting in minus seven x, which is multiplied by x plus two to get minus seven x squared minus fourteen x. Subtracting this gives eighteen x plus five. Finally, eighteen x is divided by x, yielding eighteen, which is multiplied by x plus two to get eighteen x plus thirty-six. Subtracting this from eighteen x plus five leaves a remainder of minus thirty-one. The quotient obtained from this division is two x squared minus seven x plus eighteen, and the remainder is minus thirty-one. The steps are clearly laid out in a vertical format, showing the subtraction at each stage of the long division process. Your Turn

Practice 2.4-2-1

Use the Rational Zero Theorem to find rational zero

To find rational zeros of a polynomial

  1. First, list all possible (potential) rational zeros.
  2. Then, use the Remainder Theorem to test them.

If substituting a value for [latex]x[/latex] results in a remainder of [latex]0[/latex], that value is a real zero of the polynomial.

Example 2.4-3-1: Using the rational zero theorem to final rational zeros.

[latex]f\left(x\right)=2x^4-5x^3+x^2-4[/latex]

Master L3 Key

Example 2.4-3-1: Using the rational zero theorem to final rational zeros.

[latex]f\left(x\right)=2x^4-5x^3+x^2-4[/latex]

Step 1: Find all potential zeros.

From Example 2.4-2-1 we have found the potential zeros

[latex]\frac pq=\pm1,\;\pm2,\;\pm4,\;\pm\frac12[/latex]

Step 2: use the Remainder Theorem to test them.

[latex]f\left(1\right)=2\left(1\right)^4-5\left(1\right)^3+\left(1\right)^2-4=-6[/latex]

[latex]f\left(-1\right)=2\left(-1\right)^4-5\left(-1\right)^3+\left(-1\right)^2-4=4[/latex]

[latex]f\left(-2\right)=2\left(-2\right)^4-5\left(-2\right)^3+\left(-2\right)^2-4=72[/latex]

[latex]f\left(2\right)=2\left(2\right)^4-5\left(2\right)^3+\left(2\right)^2-4=-8[/latex]

[latex]f\left(-4\right)=2\left(-4\right)^4-5\left(-4\right)^3+\left(-4\right)^2-4=844[/latex]

[latex]f\left(4\right)=2\left(4\right)^4-5\left(4\right)^3+\left(4\right)^2-4=204[/latex]

[latex]f\left(\frac12\right)=2\left(\frac12\right)^4-5\left(\frac12\right)^3+\left(\frac12\right)^2-4=-\frac{17}4[/latex]

[latex]f\left(-\frac12\right)=2\left(-\frac12\right)^4-5\left(-\frac12\right)^3+\left(-\frac12\right)^2-4=-3[/latex]

None of the rational candidates work. That means this polynomial has no rational real zeros.

The image displays the detailed steps of polynomial long division. We are dividing the polynomial, which is two x cubed minus three x squared plus four x plus five, by the binomial, which is x plus two. The process starts with two x cubed divided by x, giving two x squared, which is then multiplied by the divisor, x plus two, to get two x cubed plus four x squared. This result is subtracted from the initial terms of the dividend, leaving minus seven x squared plus four x. Next, minus seven x squared is divided by x, resulting in minus seven x, which is multiplied by x plus two to get minus seven x squared minus fourteen x. Subtracting this gives eighteen x plus five. Finally, eighteen x is divided by x, yielding eighteen, which is multiplied by x plus two to get eighteen x plus thirty-six. Subtracting this from eighteen x plus five leaves a remainder of minus thirty-one. The quotient obtained from this division is two x squared minus seven x plus eighteen, and the remainder is minus thirty-one. The steps are clearly laid out in a vertical format, showing the subtraction at each stage of the long division process. Your Turn

Practice 2.4-3-1

Use of synthetic division to divide polynomials

As we’ve seen, long division of polynomials can involve many steps and be quite cumbersome. Synthetic division is a shorthand method of dividing polynomials for the special case of dividing by a linear factor whose leading coefficient is [latex]1[/latex].

To illustrate the process, recall the example at the beginning of the section.

Divide [latex]2x^3-3x^2+4x+5[/latex] by [latex]x+2[/latex] using the long division algorithm.

The final form of the process looked like this:

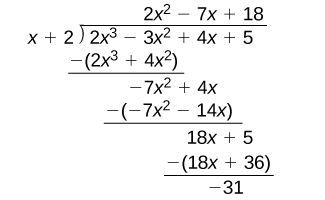
The image displays the detailed steps of polynomial long division. We are dividing the polynomial, which is two x cubed minus three x squared plus four x plus five, by the binomial, which is x plus two. The process starts with two x cubed divided by x, giving two x squared, which is then multiplied by the divisor, x plus two, to get two x cubed plus four x squared. This result is subtracted from the initial terms of the dividend, leaving minus seven x squared plus four x. Next, minus seven x squared is divided by x, resulting in minus seven x, which is multiplied by x plus two to get minus seven x squared minus fourteen x. Subtracting this gives eighteen x plus five. Finally, eighteen x is divided by x, yielding eighteen, which is multiplied by x plus two to get eighteen x plus thirty-six. Subtracting this from eighteen x plus five leaves a remainder of minus thirty-one. The quotient obtained from this division is two x squared minus seven x plus eighteen, and the remainder is minus thirty-one. The steps are clearly laid out in a vertical format, showing the subtraction at each stage of the long division process.

There is a lot of repetition in the table. If we don’t write the variables but, instead, line up their coefficients in columns under the division sign and also eliminate the partial products, we already have a simpler version of the entire problem.

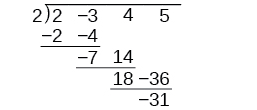
The image shows the steps of synthetic division for dividing a polynomial. The divisor is implied to be (x minus two) because the value 'two' is placed to the left of the dividend's coefficients. The coefficients of the dividend, two x cubed minus three x squared plus four x plus five, are written as 'two, minus three, four, five' under the division symbol.

Synthetic division carries this simplification even a few more steps. Collapse the table by moving each of the rows up to fill any vacant spots. Also, instead of dividing by [latex]2[/latex], as we would in division of whole numbers, then multiplying and subtracting the middle product, we change the sign of the “divisor” to [latex]–2[/latex], multiply and add. The process starts by bringing down the leading coefficient.

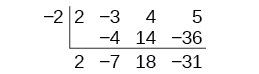
The image shows the steps of synthetic division for dividing a polynomial. The divisor is implied to be (x plus two) because the value 'minus two' is placed to the left of the dividend's coefficients. The coefficients of the dividend, two x cubed minus three x squared plus four x plus five, are written as 'two, minus three, four, five' to the right of the 'minus two'.

Synthetic Division

Synthetic division is a shortcut that can be used when the divisor is a binomial in the form [latex]x−k[/latex] where [latex]k[/latex] is a real number. In synthetic division, only the coefficients are used in the division process.

How To

Given two polynomials, use synthetic division to divide.

  1. Write [latex]k[/latex] for the divisor.
  2. Write the coefficients of the dividend.
  3. Bring the lead coefficient down.
  4. Multiply the lead coefficient by [latex]k[/latex]. Write the product in the next column.
  5. Add the terms of the second column.
  6. Multiply the result by [latex]k[/latex]. Write the product in the next column.
  7. Repeat steps 5 and 6 for the remaining columns.
  8. Use the bottom numbers to write the quotient. The number in the last column is the remainder. The next number from the right has degree [latex]0[/latex], the next number has degree [latex]1[/latex], and so on.

Example 2.4-4-1: Using Synthetic Division to Divide a Second-Degree Polynomial

Use synthetic division to divide [latex]5x^2-3x-36[/latex] by [latex]x-3[/latex].

Master L3 Key

Example 2.4-4-1: Using Synthetic Division to Divide a Second-Degree Polynomial

Use synthetic division to divide [latex]5x^2-3x-36[/latex] by [latex]x-3[/latex].

Begin by setting up the synthetic division. Write [latex]k[/latex] and the coefficients.

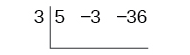
The image shows the beginning setup for synthetic division. The number 'three' is placed to the left of a vertical line, representing the root of the divisor (x minus three). To the right of the vertical line, the numbers 'five, minus three, minus thirty-six' are written, representing the coefficients of the polynomial dividend, which is likely five x squared minus three x minus thirty-six.

Bring down the lead coefficient. Multiply the lead coefficient by [latex]k[/latex].

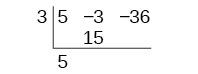
The first step of synthetic division is shown. The number 'three' is the root of the divisor. The coefficients of the dividend are 'five', 'minus three', and 'minus thirty-six'. The leading coefficient 'five' has been brought down below the horizontal line. The root 'three' is now multiplied by this 'five', resulting in 'fifteen', which is written under the next coefficient 'minus three'.

Continue by adding the numbers in the second column. Multiply the resulting number by [latex]k[/latex]. Write the result in the next column. Then add the numbers in the third column.

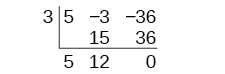
The synthetic division process is nearing completion. The root of the divisor is 'three'. The coefficients of the dividend were 'five', 'minus three', and 'minus thirty-six'. The leading coefficient 'five' was brought down. Then, 'three' was multiplied by 'five' to get 'fifteen', which was added to 'minus three' to result in 'twelve'. Now, 'three' is multiplied by 'twelve' to get 'thirty-six', which is added to 'minus thirty-six' to result in 'zero'. The numbers below the horizontal line, 'five, twelve, zero', represent the coefficients of the quotient and the remainder. The last number, 'zero', is the remainder. The other numbers, 'five' and 'twelve', are the coefficients of the quotient, which is a polynomial of one degree less than the dividend. Therefore, the quotient is five x plus twelve, and the remainder is zero. This indicates that (x minus three) is a factor of the original polynomial.

The result is [latex]5x+12[/latex]. The remainder is [latex]0[/latex]. So [latex]x−3[/latex] is a factor of the original polynomial.

Just as with long division, we can check our work by multiplying the quotient by the divisor and adding the remainder.

[latex]\left(x-3\right)\left(5x+12\right)+0=5x^2-3x-36[/latex]

Find zeros of a polynomial function

Steps to Find Real Zeros of a Polynomial

  1. List possible rational zeros

[latex]\frac pq=\pm\frac{factors\;of\;cons\tan t}{factors\;of\;leading\;coefficient}[/latex]

  1. Test values using Remainder Theorem
    Plug into the polynomial.
    If [latex]f\left(x\right)=0[/latex], then x is a real zero.
  2. Use Synthetic Division
    Divide the polynomial by opposite value of x (real zero).
    This gives a simpler polynomial. Repeat the process.
  3. Solve the remaining polynomial
    Factor or use the quadratic formula to find more zeros.

Example 2.4-5-1: Find zeros of a polynomial function

[latex]f\left(x\right)=x^3-6x^2+11x-6[/latex]

Master L3 Key

Example 2.4-4-1: Find zeros of a polynomial function

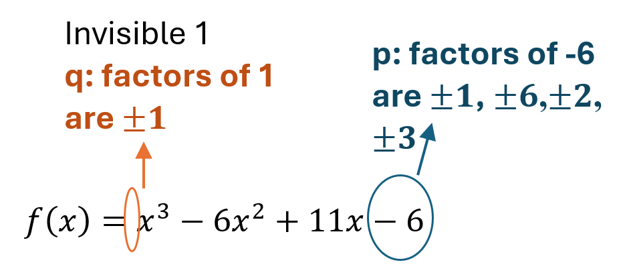
The polynomial function f(x) = x cube - 6x squared + 11x - 6 is shown. An orange arrow points to the coefficient of the x cube term, which is an invisible 1, and indicates that 'q: factors of 1 are ±1'. A blue arrow points to the constant term -6 and indicates that 'p: factors of -6 are ±1, ±6, ±2, ±3'.

  1. List possible rational zeros

[latex]\frac pq=\pm\frac{factors\;of\;cons\tan t}{factors\;of\;leading\;coefficient}[/latex]

[latex]\frac pq=\pm\frac11,\;\pm\frac61,\;\pm\frac21,\;\pm\frac31[/latex]

[latex]\frac pq=\pm1,\;\pm6,\;\pm2,\;\pm3[/latex]

  1. Test values using Remainder Theorem
    Plug into the polynomial.
    If [latex]f\left(x\right)=0[/latex], then [latex]x[/latex] is a real zero.

Test values if [latex]x=1[/latex]

[latex]f\left(1\right)=\left(1\right)^3-6\left(1\right)^2+11\left(1\right)-6=0[/latex]

Once we find one real zero, we can stop at this step and start the next step.

[latex]x=1[/latex]

  1. Use Synthetic Division
    Divide the polynomial by the value of [latex]x[/latex] we found in step 2 (real zero).
    This gives a simpler polynomial. Repeat the process.

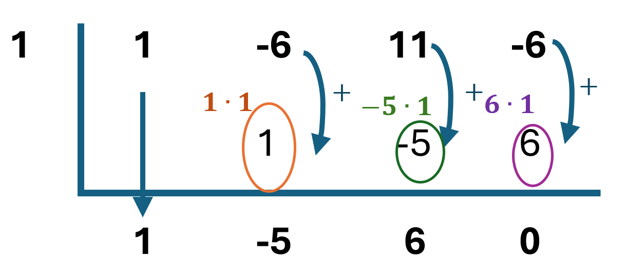
The process starts by bringing down the leading coefficient '1'. This '1' is then multiplied by the root '1', resulting in '1 ⋅ 1 = 1', which is written under the next coefficient '-6'. These two numbers are added: '-6 + 1 = -5', and the result '-5' is written below the line. Next, '-5' is multiplied by the root '1', resulting in '-5 ⋅ 1 = -5', which is written under the next coefficient '11'. These two numbers are added: '11 + (-5) = 6', and the result '6' is written below the line. Finally, '6' is multiplied by the root '1', resulting in '6 ⋅ 1 = 6', which is written under the last coefficient '-6'. These two numbers are added: '-6 + 6 = 0', and the result '0' is written below the line. The numbers below the line, '1', '-5', '6', and '0', represent the coefficients of the resulting polynomial after division by (x - 1) and the remainder. The last number, '0', is the remainder, indicating that (x - 1) is a factor of the original polynomial or that the polynomial evaluates to 0 at x = 1. The other numbers, '1', '-5', and '6', are the coefficients of the quotient, which is x squared - 5x + 6.

  1. Solve the remaining polynomial
    Factor or use the quadratic formula to find more zeros.

[latex]x^2-5x+6=0[/latex]

[latex]\left(x-2\right)\left(x-3\right)=0[/latex]

[latex]x=2,\;x=3[/latex]

Overall real zeros are: [latex]x=1,\;x=2,\;x=3[/latex]

The image displays the detailed steps of polynomial long division. We are dividing the polynomial, which is two x cubed minus three x squared plus four x plus five, by the binomial, which is x plus two. The process starts with two x cubed divided by x, giving two x squared, which is then multiplied by the divisor, x plus two, to get two x cubed plus four x squared. This result is subtracted from the initial terms of the dividend, leaving minus seven x squared plus four x. Next, minus seven x squared is divided by x, resulting in minus seven x, which is multiplied by x plus two to get minus seven x squared minus fourteen x. Subtracting this gives eighteen x plus five. Finally, eighteen x is divided by x, yielding eighteen, which is multiplied by x plus two to get eighteen x plus thirty-six. Subtracting this from eighteen x plus five leaves a remainder of minus thirty-one. The quotient obtained from this division is two x squared minus seven x plus eighteen, and the remainder is minus thirty-one. The steps are clearly laid out in a vertical format, showing the subtraction at each stage of the long division process. Your Turn

Practice 2.4-5-1

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Math Mastery Manual Copyright © by Linglin (Niki) Liu is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book