1.1: Functions

Linglin (Niki) Liu

1.1: Functions

Learning Objectives

Determine whether a relation represents a function.
Find the value of a function.
Find the domain of a function defined by an equation.
Find the result of arithmetic operations with functions.

Determining Whether a Relation Represents a Function

A relation is a set of ordered pairs. The set of the first components of each ordered pair is called the domain and the set of the second components of each ordered pair is called the range.

What is a Function

A function is a relation in which each possible input value leads to exactly one output value. We say ‘the output is a function of the input.’

The input values make up the domain, and the output values make up the range.”

Determine whether a relation represents a function

What is a Mathematical Relation, and What is a Function?

Identifying Functions.

Independent Variables: These are the values you can choose freely.
Dependent Variables: These are the outcomes (or results) that depend on the choices you make.

To better understand this concept, let’s use a real-life example:

Imagine walking into a restaurant, L3 Restaurant. Here’s how a function works in this scenario: Do not worry about the taxes, or tips or other factors.

You’re given a menu, and based on it, you place an order.

Let’s say you decide to order an appetizer Nuggets, a main course Cheeseburger, a beverage Iced Tea. The choices you make for each item are independent variables. In mathematics, we typically represent these as X.

After your meal, you receive the bill. The total amount you pay is the dependent variable, as it’s determined by the choices you made earlier. In mathematics, we represent this as Y.

This relationship, where each set of choices (X) leads to a specific outcome (Y), is called a function.

Scenario:

Imagine you and your friend decide to meet at L3 restaurant. You both ordered Iced Tea, but the system displays different prices for you and your friend’s orders. In real life, this might be referred to as a “system bug,” a “display issue,” or a “system problem.”

In here, this situation would be identified as not a function.

Here’s why:

A single input (the same order) produces multiple outputs (different prices). This violates the definition of a function, which requires that each input corresponds to exactly one output.

Example 1.1-1-1: Determine whether the relation is a function.

{(1, 3), (1, 5), (2, 4)}
{(0, 4), (1, 5), (2, 4)}

Key

Example 1.1-1-1:

{(1, 3), (1, 5), (2, 4)}

This is NOT a function. Since the same x value gives more than two y values. For example, the same product (x value) shows different prices (y values) in the same restaurant (Relation). Does this make sense? The answer is no; thus, it is a function.

{(0, 4), (1, 5), (2, 4)}

This IS a function because every x -value corresponds to only one y -value. You might wonder about the points (0,4) and (2,4). Here’s the explanation: Let’s say x represents the product and y represents the price. Is it possible for different products to have the same price at the same restaurant? The answer is yes. If this makes sense, then yes, it is a function.

Example 1.1-1-2: Determine whether the relation is a function.

$y = x^{2} - 4$
$y^{2} = x^{2} + 9$
$y^{2} = x + 6$
$x^{2} + y = 3$

Key

Example 1.1-1-2:

$y = x^{2} - 4$

Yes, it is a function. Since every x -value corresponds to only one y -value.

$y^{2} = x^{2} + 9$

No, it is NOT a function. Since every x -value corresponds to more than one y -value. For example, if x = 0, then [latex]y^2=9[/latex] , thus [latex]y=3[/latex] or [latex]y=-3[/latex] . Note: [latex]\left(3\right)^2=9[/latex] and [latex]\left(-3\right)^2=9[/latex].

$y^{2} = x + 6$

No, it is NOT a function. Since not every x -value corresponds to only one y –value. For example, if [latex]x =-6[/latex], then [latex]y^2=0[/latex], thus [latex]y=0[/latex]. However, this is just the special case, what if [latex]x=-5[/latex]? If [latex]x=-5[/latex], then [latex]y^2=1[/latex], thus [latex]y=1[/latex] or [latex]y=-1[/latex].

$x^{2} + y = 3$

Yes, it is a function. Since every -value corresponds to only one -value.

Your Turn

Practice 1.1-1-1

Find the value of a function

Function notation

The notation [latex]y=f(x)[/latex] defines a function named f . This is read as “y is a function of x .” The letter x represents the input value, or independent variable. The letter y , or f(x), represents the output value, or dependent variable.

Evaluating functions steps:

Use parentheses to substitute all x-values in the given function.
Identify the new x-value.
Substitute the new x-value inside the parentheses.
Solve the equation.

Example 1.1-2-1: Evaluate a function given by an algebraic expression.

Find [latex]f(7)[/latex] if [latex]f\left(x\right)=3x^2-1[/latex]

Key

Example 1.1-2-1: Evaluate a function given by an algebraic expression.

Find [latex]f(7)[/latex] if [latex]f\left(x\right)=3x^2-1[/latex]

Solution steps:

Step 1:Use parentheses to substitute all x-values in the given function.

[latex]f\left(\right)=3\left(\right)^2-1[/latex]

Step 2: Identify the new x-value.

New [latex]x=7[/latex], since [latex]f(x)[/latex] is rewritten as [latex]f(7)[/latex]

Step 3: Substitute the new x-value inside the parentheses.

[latex]f\left(7\right)=3\left(7\right)^2-1[/latex]

Step 4:Solve the equation.

[latex]f\left(7\right)=3\left(7\right)^2-1[/latex] (Order of operation, PEMDAS)

[latex]f\left(7\right)=3\left(49\right)-1[/latex]

[latex]f(7)=147-1[/latex]

[latex]f(7)=146[/latex]

Note: In here, [latex]f(7)[/latex] represent a function, it is just a “label”

f(x)
Function name is f	Independent variable x is 7

Example 1.1-2-2: Evaluate a function given by an algebraic expression.

Find [latex]f(-4)[/latex] if [latex]f\left(x\right)=7\left(x\right)^2+5x+2[/latex]

Key

Example 1.1-2-2: Evaluate a function given by an algebraic expression.

Find [latex]f(-4)[/latex] if [latex]f\left(x\right)=7\left(x\right)^2+5x+2[/latex]

Solution steps:

Step 1:Use parentheses to substitute all x-values in the given function.

[latex]f\left(\right)=7\left(\right)^2+5\left(\right)+2[/latex]

Step 2: Identify the new x-value.

[latex]x=-4[/latex]

Step 3: Substitute the new x-value inside the parentheses.

[latex]f\left(-4\right)=7\left(-4\right)^2+5\left(-4\right)+2[/latex]

Step 4:Solve the equation.

[latex]f\left(-4\right)=7\left(-4\right)^2+5\left(-4\right)+2[/latex] (Order of operation, PEMDAS)

[latex]f\left(-4\right)=7\left(16\right)+5\left(-4\right)+2[/latex]

[latex]f\left(-4\right)=112-20+2[/latex]

[latex]f(-4)=94[/latex]

Note: In this question, you need to pay attention to the signs. Remember “(negative) (negative) = positive, and (negative) (positive) = negative”

Your Turn

Practice 1.1-2-1

Practice 1.1-2-2

Find the domain of a function

Domain and Range

Domain refers to the set of all independent/input values (often denoted as x) that a function can be used.

Range refers to the set of all dependent/ output values (often denoted as y) that the function can produce based on the inputs from the domain.

Why is the domain very important? In determining domains and ranges, we need to consider what is physically possible or meaningful. For example, if you go to Best Buy (an electronics store) and ask for a burger, this is a situation where you are applying the independent variable (order a burger) into a function (the store) that is not providing the service, and then saying that the price/result (output) is not right.

Example 1.1-3-1: Find the domain of the following function

{(2, 10), (3, 10), (4, 20), (5, 30), (6, 40)}

Key

Example 1.1-3-1:

First, identify the input values. The input value is the first coordinate in an ordered pair. There are no restrictions, as the ordered pairs are simply listed. The domain is the set of the first coordinates of the ordered pairs.

{2, 3, 4, 5, 6}

Notations to Specify Domain and Range

We can write the domain and range in interval notation, which uses values within brackets to describe a set of numbers. In interval notation, we use a square bracket [ when the set includes the endpoint and a parenthesis ( to indicate that the endpoint is either not included or the interval is unbounded.

Before we begin, let us review the conventions of interval notation:

The smallest term from the interval is written first.
The largest term in the interval is written second, following a comma.
Parentheses, ( or ), are used to signify that an endpoint is not included, called exclusive.
Brackets, [ or ], are used to indicate that an endpoint is included, called inclusive.

Inequality	Interval Notation	Description
x > a	(a, ∞)	x is greater than a
x < a	(-∞, a)	x is less than a
x ≥ a	[a, ∞)	x is greater than or equal to a
x ≤ a	(-∞, a]	x is less than or equal to a
a < x < b	(a, b)	x is strictly between a and b
a ≤ x < b	[a, b)	x is between a and b, to include a
a < x ≤ b	(a, b]	x is between a and b, to include b
a ≤ x ≤ b	[a, b]	x is between a and b, to include a and b

Example 1.1-3-2: Use interval notation to represent the inequality of the x values

[latex]-3\leq x<5[/latex]
[latex]3>x[/latex]
[latex]-3\leq x[/latex]

Key

Example 1.1-3-2:

Use interval notation to represent the inequality of the x values:

[latex]-3\leq x<5[/latex]

Graph on the numbers

x is between 3 and 5, to include 3

Note: when use interval notation, the order must be from the smallest to the greatest and separate with comma. If the part has an equal sign relating to that number, we use brackets; if there is no equal sign, we use parentheses, as shown in the picture.

Answer: [-3, 5)

[latex]3>x[/latex]

A number line representing x is less than 3.

Note: For inequalities, the ‘open mouth’ side represents the greater number. For example, in [latex]3>x[/latex], we read it as ‘3 is greater than x.’ If we have [latex]3< x[/latex], we read it as ‘3 is less than x.

Answer: [latex]\left(-\infty,\;3\right)[/latex]

[latex]-3\leq x[/latex]

A number line representing x is greater than or equal to -3.

Note:always use parentheses for infinity.

Answer: [latex]\left[-3,\;\infty\right][/latex]

Using Notations to Specify Domain and Range

We can also use inequalities, or other statements that might define sets of values or data, to describe the behavior of the variable in set-builder notation. For example, [latex]\left\{x\vert10\leq x<30\right\}[/latex] describes the behavior of 𝑥 in set-builder notation. The braces {} are read as “the set of,” and the vertical bar | is read as “such that,” so we would read [latex]\left\{x\vert10\leq x<30\right\}[/latex] as “the set of x-values such that 10 is less than or equal to 𝑥, and 𝑥 is less than 30.”

For [latex]\left\{x\vert10\leq x<30\right\}[/latex], if you feel it is too complicated to read, You can think of it as set builder notation [latex]\left\{x\vert10\leq x<30\right\}[/latex] x is between 10 and 30, including 10.

Set-builder notation, and interval notation

Inequality Notation	Set-builder Notation	Interval Notation
5 < h ≤ 10	{h \| 5 < h ≤ 10}	(5, 10]
5 ≤ h < 10	{h \| 5 ≤ h < 10}	[5, 10)
5 < h < 10	{h \| 5 < h < 10}	(5, 10)
h < 10	{h \| h < 10}	(-∞, 10)
h ≥ 10	{h \| h ≥ 10}	[10, ∞)
All real numbers	[latex]\mathbb{R}[/latex]	(-∞, ∞)

Example 1.1-3-3: Using inequality notation, set-builder notation, and interval notation

A number line representing x is between 1 and 3, to include 1 and 3, or x is greater than 5.

Inequality notation: __________________________

Set-builder notation: ___________________________

Interval notation: ___________________________

Key

Example 1.1-3-3:

Using inequality notation, set-builder notation, and interval notation.

A number line representing x is between 1 and 3, to include 1 and 3, or x is greater than 5.

Inequality notation: 1 ≤ x ≤ 3, 5 < x

Set-builder notation: {x | 1 ≤ x ≤ 3, 5 < x}

Interval notation: [1, 3], (5, ∞)

Note: In here, we used a comma to separate the answer. However, some books may require it to be done differently. This depends on the software you are using and the requirements of your teacher/instructor/professor.

Another format:

Inequality notation: 1 ≤ x ≤ 3 or 5 < x

Set-builder notation: {x | 1 ≤ x ≤ 3 or 5 < x}

Interval notation: [1, 3] ∪ (5, ∞)

Finding Domain Algebraically

Commonly used restrictions

Restrictions on the domain of a function:

Denominator ≠ 0
Interior of even roots ≥ 0
Argument of logarithm > 0 (in a later section)

Steps for Finding the Domain of a Function Defined by an Equation

Start with a domain of “all real numbers”.
Look for restrictions.
- If restriction does not apply, then the domain is all real numbers.
- If there is(are) restriction(s), apply restrictions, set up equation and solve for x. combine the answers.

Since we are now in the Linear City, thus we might ignore the logarithm for now. When trying to find the domain, ask yourself 2 questions.

Any fraction? Do I see [latex]\frac ba[/latex]

If yes, then [latex]a\neq0[/latex]

Any even root? Do I see [latex]\sqrt a[/latex]

Example 1.1-3-4: Find the domain of the following functions, then use set builder notation and interval notation represent its domain.

[latex]F\left(x\right)=x^2-x[/latex]

Key

Example 1.1-3-4:

Find the domain of the following functions, then use set builder notation and interval notation represent its domain.

[latex]F\left(x\right)=x^2-x[/latex]

Step 1: Start with a domain of “all real numbers”.

Step 2: Look for restrictions.

Do I see [latex]\frac ba[/latex]? No, then skip.
Do I see [latex]\sqrt a[/latex]? No, then skip.
Overall, no restrictions apply.
Thus, domain x is all real numbers.

Answer:

Set builder notation: [latex]\left\{x\vert x\in\mathbb{R}\right\}[/latex]

Interval notation: [latex]\left(-\infty,\;\infty\right)[/latex]

Example 1.1-3-5: Find the domain of the following functions, then use set builder notation and interval notation represent its domain.

[latex]F(x)=\frac x{3x-1}[/latex]

Key

Example 1.1-3-5:

Find the domain of the following functions, then use set builder notation and interval notation represent its domain.

[latex]F(x)=\frac x{3x-1}[/latex]

Step 1: Start with a domain of “all real numbers”.

Step 2: Look for restrictions.

Do I see [latex]\frac ba[/latex]?
Then [latex]a\neq0[/latex]
[latex]3x-1\neq0[/latex] (Add 1 on both sides of the equal sign.)
[latex]3x\neq1[/latex] (Divide 3 on both sides of the equal sign.)
[latex]x\neq\frac13[/latex]
Do I see [latex]\sqrt a[/latex]? No, then skip.
Overall, no restrictions apply.
Thus, domain x is all real numbers.

Answer:

Set builder notation: [latex]\left\{x\vert x\in\mathbb{R}\right\}[/latex]

Interval notation: [latex]\left(-\infty,\;\infty\right)[/latex]

Your Turn

Practice 1.1-3-1 | Practice 1.1-3-2 | Practice 1.1-3-3

Find the result of arithmetic operations with functions

Arithmetic Combinations of Functions

If two functions have a common domain, then arithmetic can be performed with them using the following definitions.

[latex]\left(f+g\right)\left(x\right)=f\left(x\right)+g\left(x\right)[/latex]

[latex]\left(f-g\right)\left(x\right)=f\left(x\right)-g\left(x\right)[/latex]

[latex]\left(f\cdot g\right)\left(x\right)=f\left(x\right)\cdot g\left(x\right)[/latex]

[latex]\left(\frac fg\right)\left(x\right)=\frac{f\left(x\right)}{g\left(x\right)};\;where\;g\left(x\right)\neq0[/latex]

The domain of [latex]\left(f+g\right),\;\left(f-g\right),\;\left(f\cdot g\right)[/latex] is the common domains of fand g.

* The domain of [latex]\left(\frac fg\right)[/latex] is the common domains of f and g AND [latex]g\left(x\right)\neq0[/latex].

Arithmetic Operations Steps:

Identify what is the operation between two functions are add, subtracting, multiplying or dividing.
Write two functions and use required operation you found in step 1.
Solve and simplify.

Dr. Linear

In step 2, it would be a good idea to have parentheses to separate the two functions. The reason for doing so is that if you have subtraction, there will be sign changes. If you have multiplication, FOIL might be involved.

For example: [latex]f\left(x\right)=x+3,\;g\left(x\right)=x-7[/latex], if we need to find [latex]\left(f-g\right)\left(x\right)[/latex]

Identify what is the operation between two functions are add, subtracting, multiplying or dividing.

Subtraction: use –

Write two functions and use required operation you found in step 1.[latex]f\left(x\right)-g\left(x\right)=\left(x+3\right)-\left(x-7\right)[/latex]
Solve and simplify.

[latex]f\left(x\right)-g\left(x\right)=\left(x+3\right)-\left(x-7\right)[/latex]

[latex]f\left(x\right)-g\left(x\right)=x+3-x+7[/latex]

[latex]f\left(x\right)-g\left(x\right)=10[/latex]

In this question, if you do not use parentheses, more likely you will make sign mistake as it shows:

[latex]f\left(x\right)-g\left(x\right)=x+3-x-7[/latex]

[latex]f\left(x\right)-g\left(x\right)=-4[/latex] (Wrong Answer)

Example 1.1-4-1:

Given functions [latex]f\left(x\right)=3x+1;\;g\left(x\right)=2x-5[/latex]

Find [latex]\left(f+g\right)\left(x\right)[/latex] and its domain.

[latex]\left(f+g\right)\left(x\right)[/latex] = ______________________.

Domain: ______________

Find [latex]\left(f-g\right)\left(x\right)[/latex] and its domain.

[latex]\left(f-g\right)\left(x\right)[/latex] = ______________________.

Domain: ______________

Find [latex]\left(f\cdot g\right)\left(x\right)[/latex] and its domain.

[latex]\left(f\cdot g\right)\left(x\right)[/latex] = ______________________.

Domain: ______________

Find [latex]\left(\frac fg\right)\left(x\right)[/latex] and its domain.

[latex]\left(\frac fg\right)\left(x\right)[/latex] = ______________________.

Domain: ______________

Key

Example 1.1-4-1:

Given functions [latex]f\left(x\right)=3x+1;\;g\left(x\right)=2x-5[/latex]

Find [latex]\left(f+g\right)\left(x\right)[/latex] and its domain.

1. Identify what is the operation between two functions are add, subtracting, multiplying or dividing.

Adding: use +

1. Write two functions and use required operation you found in step 1.

[latex]f\left(x\right)+g\left(x\right)=\left(3x+1\right)+\left(2x-5\right)[/latex]

1. Solve and simplify.

[latex]f\left(x\right)+g\left(x\right)=\left(3x+1\right)+\left(2x-5\right)[/latex]

[latex]f\left(x\right)+g\left(x\right)=3x+1+2x-5[/latex]

Only addition, thus we can remove the parentheses without making any changes.

[latex]f\left(x\right)+g\left(x\right)=5x-4[/latex]

Domain:

Check domain for [latex]f\left(x\right)=3x+1[/latex]

Step 1:Start with a domain of “all real numbers”.

Step 2: Look for restrictions.

Do I see [latex]\frac ba[/latex]? No, then skip.
Do I see [latex]\sqrt a[/latex]? No, then skip.
Overall, no restrictions apply.
Thus, domain x is all real numbers.

Check domain for [latex]g\left(x\right)=2x-5[/latex]

Step 1:Start with a domain of “all real numbers”.

Step 2: Look for restrictions.

Do I see [latex]\frac ba[/latex]? No, then skip.
Do I see [latex]\sqrt a[/latex]? No, then skip.
Overall, no restrictions apply.
Thus, domain x is all real numbers.

Common domains of f and g are all real numbers.

Answer:

[latex]\left(f+g\right)\left(x\right)=5x-4[/latex]

Domain:

Set builder notation: [latex]\left\{x\vert x\in\mathbb{R}\right\}[/latex]

Interval notation: [latex]\left(-\infty,\;\infty\right)[/latex]

Find [latex]\left(f-g\right)\left(x\right)[/latex] and its domain.

1. Identify what is the operation between two functions are add, subtracting, multiplying or dividing.

Subtraction: use –

1. Write two functions and use required operation you found in step 1.

[latex]f\left(x\right)-g\left(x\right)=\left(3x+1\right)-\left(2x-5\right)[/latex]

1. Solve and simplify.

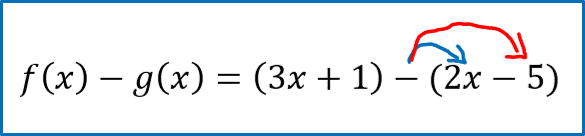
Subtraction of two functions, f of x minus g of x, which is equal to the quantity three x plus one minus the quantity two x minus five.

↓

[latex]f\left(x\right)-g\left(x\right)=\left(3x+1\right)-\left(2x-5\right)[/latex]

[latex]f\left(x\right)-g\left(x\right)=3x+1-{\color[rgb]{0.0, 0.44, 0.73}\mathbf2}{\color[rgb]{0.0, 0.44, 0.73}\boldsymbol x}+{\color[rgb]{0.86, 0.0, 0.0}\mathbf5}[/latex]

[latex]f\left(x\right)-g\left(x\right)=x+6[/latex]

Domain:

Check domain for [latex]f\left(x\right)=3x+1[/latex]

Step 1:Start with a domain of “all real numbers”.

Step 2: Look for restrictions.

Do I see [latex]\frac ba[/latex]? No, then skip.
Do I see [latex]\sqrt a[/latex]? No, then skip.
Overall, no restrictions apply.
Thus, domain x is all real numbers.

Check domain for [latex]g\left(x\right)=2x-5[/latex]

Step 1:Start with a domain of “all real numbers”.

Step 2: Look for restrictions.

Do I see [latex]\frac ba[/latex]? No, then skip.
Do I see [latex]\sqrt a[/latex]? No, then skip.
Overall, no restrictions apply.
Thus, domain x is all real numbers.

Common domains of f and g are all real numbers.

Answer:

[latex]\left(f-g\right)\left(x\right)=x+6[/latex]

Domain:

Set builder notation: [latex]\left\{x\vert x\in\mathbb{R}\right\}[/latex]

Interval notation: [latex]\left(-\infty,\;\infty\right)[/latex]

Find [latex]\left(f\cdot g\right)\left(x\right)[/latex] and its domain.

1. Identify what is the operation between two functions are add, subtracting, multiplying or dividing.

Multiplying: use ∙ (multiplication)

1. Write two functions and use required operation you found in step 1.

[latex]f\left(x\right)\cdot g\left(x\right)=\left(3x+1\right)\left(2x-5\right)[/latex]

1. Solve and simplify.

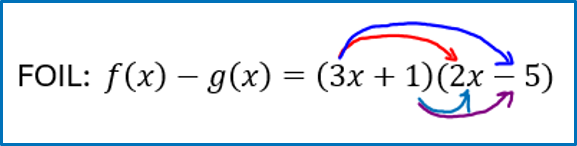
The image shows the multiplication of two binomials using the FOIL method. The expression is f of x times g of x, which is equal to the quantity three x plus one multiplied by the quantity two x minus five.

↓

[latex]f\left(x\right)\cdot g\left(x\right)=\left(3x+1\right)\left(2x-5\right)[/latex]

[latex]f\left(x\right)\cdot g\left(x\right)={\color[rgb]{0.86, 0.0, 0.0}\mathbf6}{\color[rgb]{0.86, 0.0, 0.0}\boldsymbol x}^{\color[rgb]{0.86, 0.0, 0.0}\mathbf2}{\color[rgb]{0.0, 0.0, 1.0}\mathbf-}{\color[rgb]{0.0, 0.0, 1.0}\mathbf15}{\color[rgb]{0.0, 0.0, 1.0}\boldsymbol x}{\color[rgb]{0.0, 0.44, 0.73}\mathbf+}{\color[rgb]{0.0, 0.44, 0.73}\mathbf2}{\color[rgb]{0.0, 0.44, 0.73}\boldsymbol x}{\color[rgb]{0.5, 0.0, 0.5}\mathbf-}{\color[rgb]{0.5, 0.0, 0.5}\mathbf5}[/latex]

[latex]f\left(x\right)\cdot g\left(x\right)=6x^2-13x-5[/latex]

Domain:

Check domain for [latex]f\left(x\right)=3x+1[/latex]

Step 1:Start with a domain of “all real numbers”.

Step 2: Look for restrictions.

Do I see [latex]\frac ba[/latex]? No, then skip.
Do I see [latex]\sqrt a[/latex]? No, then skip.
Overall, no restrictions apply.
Thus, domain x is all real numbers.

Check domain for [latex]g\left(x\right)=2x-5[/latex]

Step 1:Start with a domain of “all real numbers”.

Step 2: Look for restrictions.

Do I see [latex]\frac ba[/latex]? No, then skip.
Do I see [latex]\sqrt a[/latex]? No, then skip.
Overall, no restrictions apply.
Thus, domain x is all real numbers.

Common domains of f and g are all real numbers.

Answer:

[latex]f\left(x\right)\cdot g\left(x\right)=6x^2-13x-5[/latex]

Domain:

Set builder notation: [latex]\left\{x\vert x\in\mathbb{R}\right\}[/latex]

Interval notation: [latex]\left(-\infty,\;\infty\right)[/latex]

Find [latex]\left(\frac fg\right)\left(x\right)[/latex] and its domain.

1. Identify what is the operation between two functions are add, subtracting, multiplying or dividing.

Dividing: use ÷

1. Write two functions and use required operation you found in step 1.[latex]\frac{f\left(x\right)}{g\left(x\right)}=\frac{\left(3x+1\right)}{\left(2x-5\right)}[/latex]
2. Solve and simplify.

[latex]\frac{f\left(x\right)}{g\left(x\right)}=\frac{\left(3x+1\right)}{\left(2x-5\right)}[/latex]

No common divisor or factors, thus this is the simplest form

[latex]\frac{f\left(x\right)}{g\left(x\right)}=\frac{3x+1}{2x-5}[/latex]

Domain:

Check domain for [latex]f\left(x\right)=3x+1[/latex]

Step 1:Start with a domain of “all real numbers”.

Step 2: Look for restrictions.

Do I see [latex]\frac ba[/latex]? No, then skip.
Do I see [latex]\sqrt a[/latex]? No, then skip.
Overall, no restrictions apply.
Thus, domain x is all real numbers.

Check domain for [latex]g\left(x\right)=2x-5[/latex]

Step 1:Start with a domain of “all real numbers”.

Step 2: Look for restrictions.

Do I see [latex]\frac ba[/latex]? No, then skip.
Do I see [latex]\sqrt a[/latex]? No, then skip.
Overall, no restrictions apply.
Thus, domain x is all real numbers.

Common domains of f and g are all real numbers.

Since the domain of [latex][/latex] is the common domains of f and gAND [latex]{\color[rgb]{0.0, 0.44, 0.73}\boldsymbol g}\mathbf{\color[rgb]{0.0, 0.44, 0.73}\left(x\right)}{\color[rgb]{0.0, 0.44, 0.73}\mathbf\neq}{\color[rgb]{0.0, 0.44, 0.73}\mathbf0}[/latex].

We need to include [latex]g\left(x\right)\neq0[/latex].

[latex]g\left(x\right)=2x-5[/latex]

[latex]2x-5\neq0[/latex]

[latex]2x\neq5[/latex]

[latex]x\neq\frac52[/latex]

Overall, domains of f and g are all real numbers and [latex]x\neq\frac52[/latex]

Answer:

[latex]\left(\frac fg\right)\left(x\right)=\frac{3x+1}{2x-5}[/latex]

Domain:

Set builder notation: [latex]\left\{x\vert x\neq\frac52\right\}[/latex]

Interval notation: [latex]\left(-\infty,\frac52\right),\;\left(\frac52,\;\infty\right)[/latex]

Example 1.1-4-2:

Given functions [latex]f\left(x\right)=2x^3+1;\;g\left(x\right)=x-3[/latex]

Find [latex]\left(f+g\right)\left(1\right).[/latex]
Find [latex]\left(f\cdot g\right)\left(3\right).[/latex]

Key

Example 1.1-4-2:

Given functions [latex]f\left(x\right)=2x^3+1;\;g\left(x\right)=x-3[/latex]

Find [latex]\left(f+g\right)\left(1\right).[/latex]

Step 1: Find [latex]f\left(1\right)[/latex]

[latex]f\left(1\right)=2\left(1\right)^3+1[/latex]

[latex]f\left(1\right)=2+1[/latex]

[latex]f\left(1\right)=3[/latex]

Step 2: Find [latex]g\left(1\right)[/latex]

[latex]g\left(1\right)=1-3[/latex]

[latex]g\left(1\right)=-2[/latex]

Step 3: Find [latex]\left(f+g\right)\left(1\right)[/latex]

[latex]\left(f+g\right)\left(1\right)=f\left(1\right)+g\left(1\right)[/latex]

[latex]\left(f+g\right)\left(1\right)=3+\left(-2\right)[/latex]

[latex]\left(f+g\right)\left(1\right)=3-2[/latex]

[latex]\left(f+g\right)\left(1\right)=1[/latex]

Find [latex]\left(f\cdot g\right)\left(3\right).[/latex]

Step 1: Find [latex]f\left(3\right)[/latex]

[latex]f\left(3\right)=2\left(3\right)^3+1[/latex]

[latex]f\left(3\right)=2\left(27\right)+1[/latex]

[latex]f\left(3\right)=54+1[/latex]

[latex]f\left(3\right)=55[/latex]

Step 2: Find [latex]g\left(3\right)[/latex]

[latex]g\left(3\right)=3-3[/latex]

[latex]g\left(3\right)=0[/latex]

Step 3: Find [latex]\left(f\cdot g\right)\left(3\right)[/latex]

[latex]\left(f\cdot g\right)\left(3\right)=f\left(3\right)g\left(3\right)[/latex]

[latex]\left(f\cdot g\right)\left(3\right)=\left(55\right)\left(0\right)[/latex]

Learning Objectives

What is a Function

Determine whether a relation represents a function

What is a Mathematical Relation, and What is a Function?

Scenario:

Here’s why:

Key

Key

Your Turn

Practice 1.1-1-1

Find the value of a function

Function notation

Evaluating functions steps:

Key

Key

Your Turn

Practice 1.1-2-1

Practice 1.1-2-2

Find the domain of a function

Domain and Range

Key

Notations to Specify Domain and Range

Key

Using Notations to Specify Domain and Range

Set-builder notation, and interval notation

Key

Finding Domain Algebraically

Commonly used restrictions

Steps for Finding the Domain of a Function Defined by an Equation

Key

Key

Your Turn

Practice 1.1-3-1 | Practice 1.1-3-2 | Practice 1.1-3-3

Find the result of arithmetic operations with functions

Arithmetic Combinations of Functions

Arithmetic Operations Steps:

Key

Key

Your Turn

Practice 1.1-4-1

Your Turn

Practice 1.1-4-2

Your Turn

Practice 1.1-4-3

License

Share This Book