"

1.2: The graph of a function

Learning Objectives

  1. Determine when a graph is a function.
  2. Identify information from or about a graph (Domain and Range).
  3. Find the zeros or intercepts from or about a function and its graph.

Determine when a graph is a function

The vertical line test can be used to determine whether a graph represents a function. If we can draw any vertical line that intersects a graph more than once, then the graph does not define a function because a function has only one output value for each input value.

Steps:

Master L3

Given a graph, use the vertical line test to determine if the graph represents a function.

  1. Inspect the graph to see if any vertical line drawn would intersect the curve more than once.
  2. If there is any such line, determine that the graph does not represent a function.

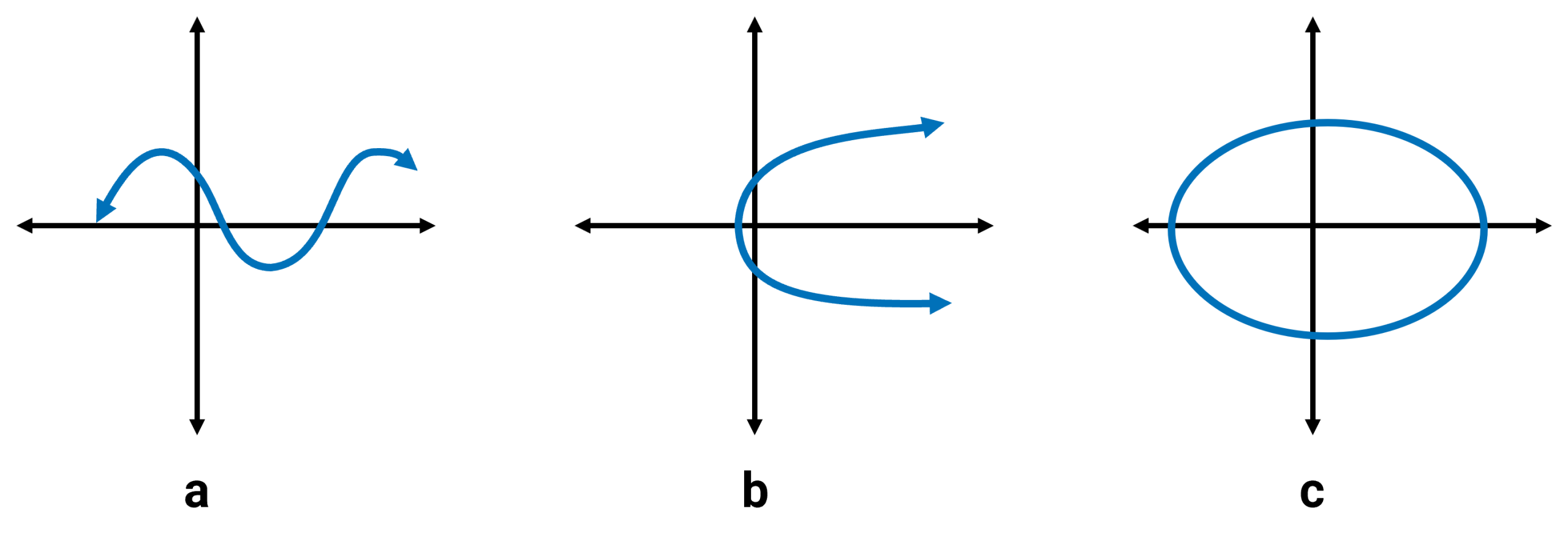
Example 1.2-1-1: Determine if it’s a function.

Three graphical representations, each attempting to depict a relationship that may or may not represent a function. The leftmost graph shows a wavy, continuous blue line that starts from the left and oscillates up and down as it moves towards the right, ending with an arrowhead pointing to the right. This suggests a relationship where for each input value along the horizontal axis, there is a corresponding output value along the vertical axis. The central graph illustrates a blue curve resembling a sideways parabola opening to the left. In this case, some input values would correspond to two different output values. The rightmost graph shows an ellipse. In this representation, for many input values (except for the leftmost and rightmost points of the ellipse), there would be two corresponding output values (an upper and a lower point on the circle).

Master L3 Key

Example 1.2-1-1:

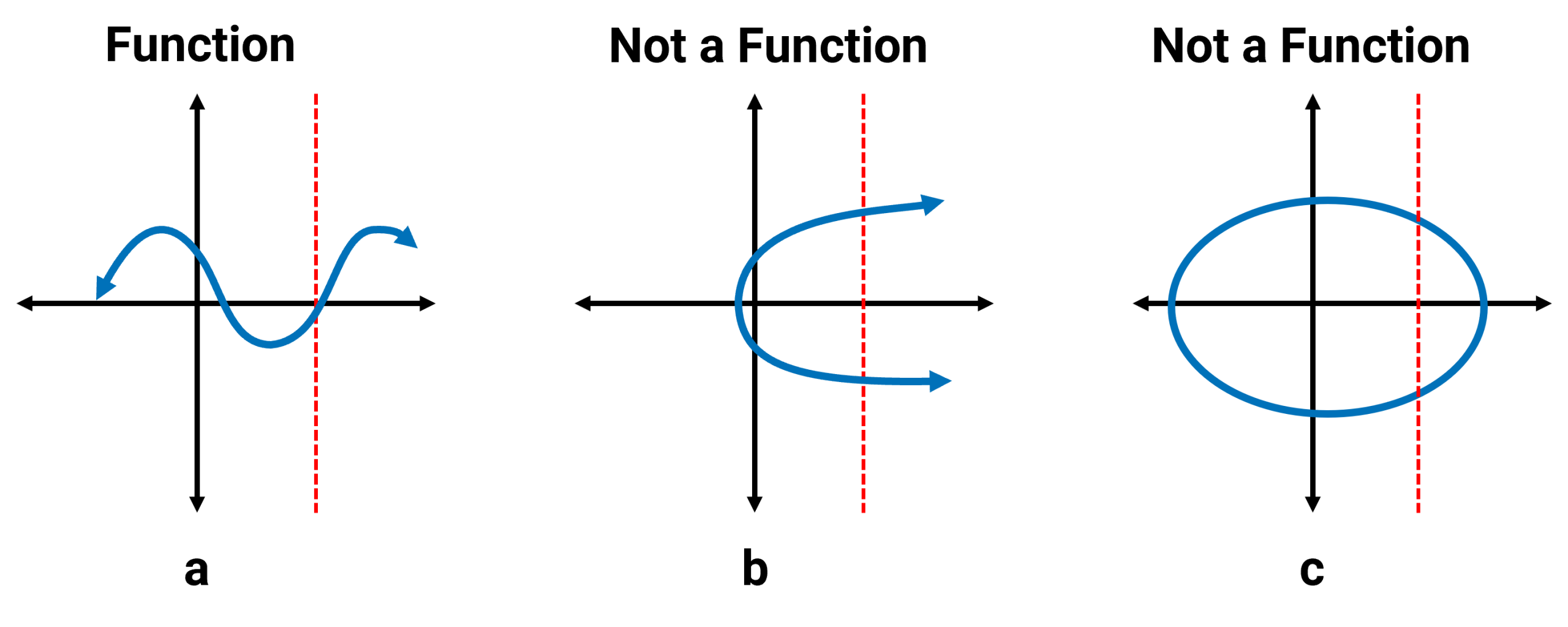
Three graphical representations, each attempting to depict a relationship that may or may not represent a function. A vertical red dashed line is superimposed on each graph to illustrate the vertical line test. This vertical red dashed line helps to visually determine if any single input value on a hypothetical horizontal axis corresponds to more than one output value on a hypothetical vertical axis. The leftmost graph shows a wavy, continuous blue line that starts from the left and oscillates up and down as it moves towards the right, ending with an arrowhead pointing to the right. The vertical red dashed line intersects the blue line at only one point. This suggests a relationship where each input value along the horizontal axis corresponds to a single output value along the vertical axis, thus representing a function according to the vertical line test. The central graph illustrates a blue curve resembling a sideways parabola opening to the left. The vertical red dashed line intersects the blue curve at two distinct points. In this case, the single input value where the red line is drawn corresponds to two different output values, indicating that this graph does not represent a function according to the vertical line test. The rightmost graph shows an ellipse. The vertical red dashed line intersects the blue ellipse at two distinct points. In this representation, the single input value where the red line is drawn corresponds to two different output values (an upper and a lower point on the ellipse), indicating that this graph does not represent a function according to the vertical line test.

Graph a is a function because, when you move a vertical line across the graph, you see only one intersection point at every position. This means it passes the vertical line test.

Graphs b and graph c are not functions because there are points where the vertical line intersects the graph more than once.

Note: Even though there may be points where the graph intersects the vertical line only once, a graph is considered a function only if the entire graph passes the vertical line test — not just at a single point. Again, the whole graph must pass the test.

Three graphical representations, each attempting to depict a relationship that may or may not represent a function. The leftmost graph shows a wavy, continuous blue line that starts from the left and oscillates up and down as it moves towards the right, ending with an arrowhead pointing to the right. This suggests a relationship where for each input value along the horizontal axis, there is a corresponding output value along the vertical axis. The central graph illustrates a blue curve resembling a sideways parabola opening to the left. In this case, some input values would correspond to two different output values. The rightmost graph shows an ellipse. In this representation, for many input values (except for the leftmost and rightmost points of the ellipse), there would be two corresponding output values (an upper and a lower point on the circle). Your Turn

Practice 1.2-1-1

Identify information from or about a graph (Domain and Range)

The domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x-axis. The range is the set of possible output values, which are all the output values shown on the y-axis.

Keep in mind that if the graph continues beyond the portion of the graph we can see, the domain and range may be greater than the visible values.

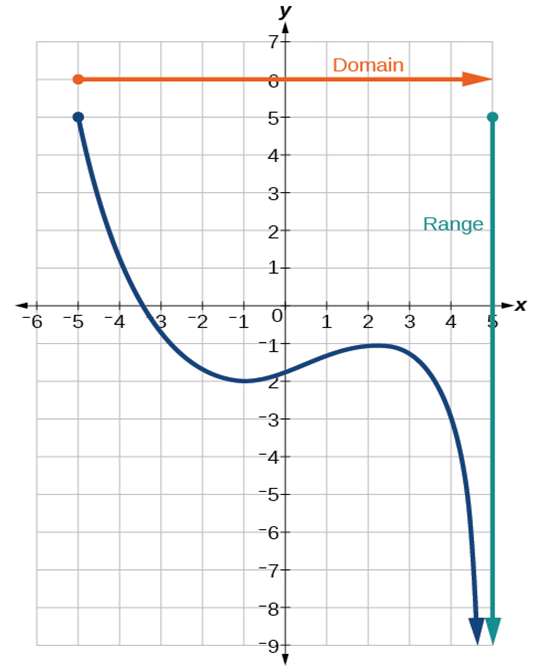
A graph of a function on a Cartesian plane with labeled x and y axes, extending from -6 to 5 on the x-axis and -9 to 7 on the y-axis. The graph itself is a continuous dark blue curve. It starts at a closed circle at (-5, 5), curves downwards passing through roughly (-3.5, 0), reaches a local minimum around (-1, -2), then increases to a local maximum around (2, -1), and finally decreases sharply. An orange arrow labeled "Domain" starts at x = -5 and extends to the right, indicating the set of all possible x-values for the function. A teal arrow labeled "Range" starts at approximately y = 5 and extends downwards, indicating the set of all possible y-values for the function.

Character
We can observe that the graph extends horizontally from -5 to the right without bound, so the domain is [−5,∞). The vertical extent of the graph is all range values 5 and below, so the range is (−∞,5].
Note that the domain and range are always written from smaller to larger values, or from left to right for domain, and from the bottom of the graph to the top of the graph for range.

Example 1.2-2-1: Find the domain and range of the function 𝑓 whose graph is shown.

A graph of a function labeled 'f' on a Cartesian plane with labeled x and y axes, extending from -3 to 2 on the x-axis and -6 to 2 on the y-axis. The graph itself is a continuous dark blue curve. It starts with an open circle at x = -3 and approximately y = 0, curves downwards to a minimum at (-2, -4), then increases, reaches a local maximum around (0, 0), and then decreases to a closed circle at x = 1 and y = -4. The open circle at x = -3 indicates that this x-value is not included in the domain, while the closed circle at x = 1 indicates that this x-value is included in the domain.

Master L3 Key

Example 2-2-1:

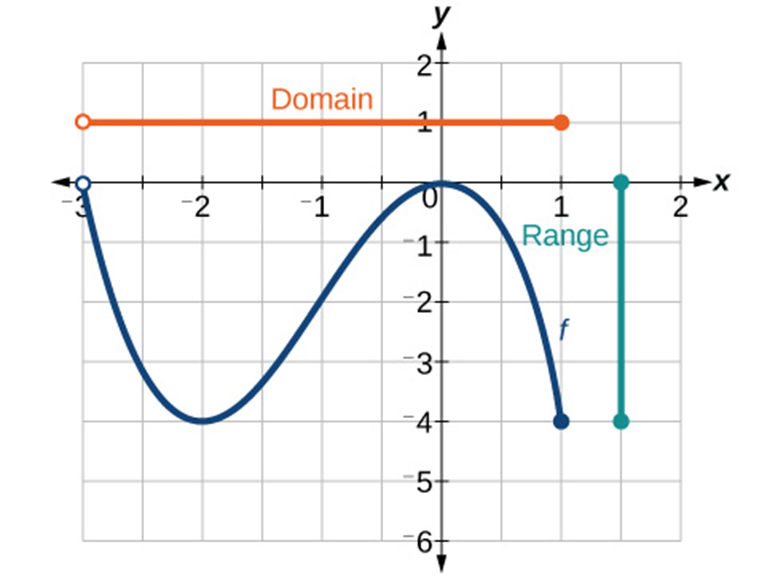
A graph of a function labeled 'f' on a Cartesian plane with labeled x and y axes, extending from -3 to 2 on the x-axis and -6 to 2 on the y-axis. The graph itself is a continuous dark blue curve. It starts with an open circle at x = -3 and approximately y = 0, curves downwards to a minimum at (-2, -4), then increases, reaches a local maximum around (0, 0), and then decreases to a closed circle at x = 1 and y = -4. The open circle at x = -3 indicates that this x-value is not included in the domain, while the closed circle at x = 1 indicates that this x-value is included in the domain. An orange horizontal line segment labeled "Domain" extends from an open circle at x = -3 to a closed circle at x = 1. A teal vertical line segment labeled "Range" extends from a closed circle at y = -4 to a closed circle at approximately y = 0.

The horizontal extent of the graph is –3 to 1, so the domain of 𝑓 is (−3,1]. The vertical extent of the graph is 0 to –4, so the range is [−4,0].

Three graphical representations, each attempting to depict a relationship that may or may not represent a function. The leftmost graph shows a wavy, continuous blue line that starts from the left and oscillates up and down as it moves towards the right, ending with an arrowhead pointing to the right. This suggests a relationship where for each input value along the horizontal axis, there is a corresponding output value along the vertical axis. The central graph illustrates a blue curve resembling a sideways parabola opening to the left. In this case, some input values would correspond to two different output values. The rightmost graph shows an ellipse. In this representation, for many input values (except for the leftmost and rightmost points of the ellipse), there would be two corresponding output values (an upper and a lower point on the circle). Your Turn

Practice 1.2-2-1

Practice 1.2-2-2

Practice 1.2-2-3

Practice 1.2-2-4

Find the zeros or intercepts from or about a function and its graph

x-intercept

The point on the graph of a function when the output value is 0; the point at which the graph crosses the horizontal axis.

y-intercept

The value of a function when the input value is zero; also known as initial value.

Master L3
Note: A function can have zero or one y-intercept, and zero, one, or more x-intercepts.

Example 1.2-3-1: Find the x-intercept(s) and y-intercept.

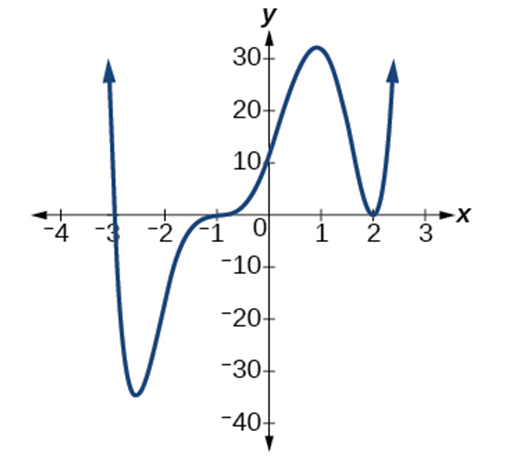
x-intercepts: -3,-1,2 at (-3,0),(-1,0),(2,0).

y-intercepts: 10 at (0,10).

Recall the formatting of Coordinates/Ordered Pair:

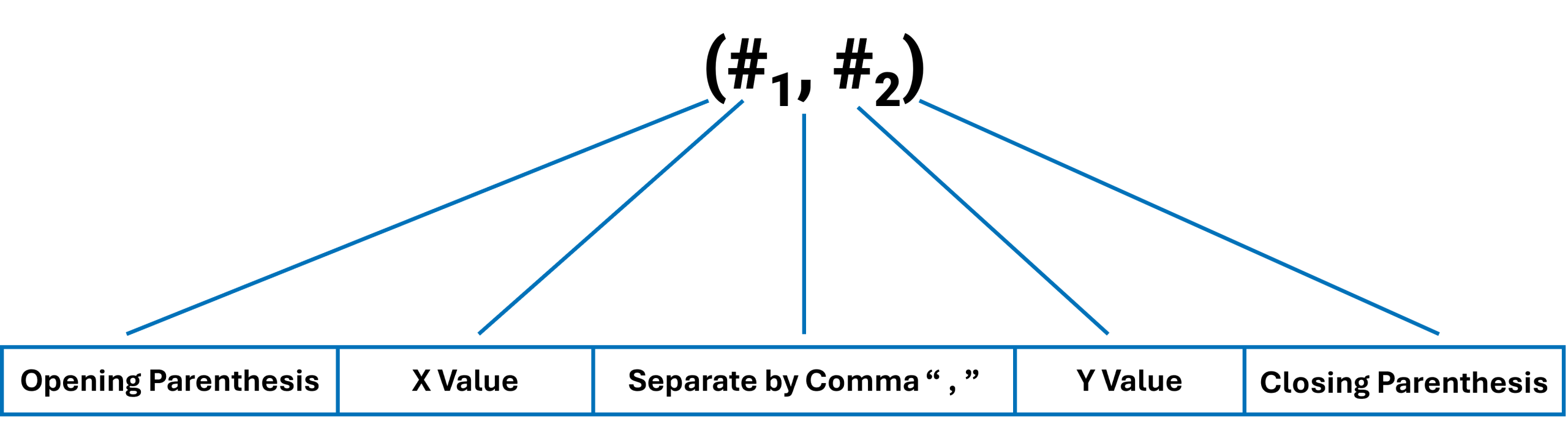
As we can see, when finding the x-intercept, the y-value is always 0. This is the point where the graph touches or crosses the x-axis. When finding the y-intercept, the x-value is always 0, which is when the graph touches or crosses the y-axis.

Example 1.2-3-2: Find the x-intercept(s) and y-intercept.

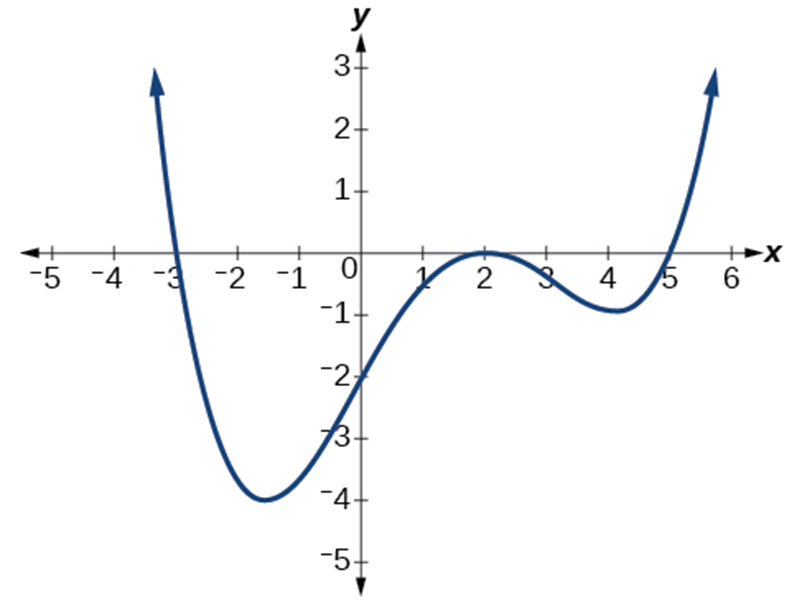
x-intercepts: 3,2,5 at (-3,0),(2,0),(5,0).

y-intercepts: -2 at (0,-2).

To find the x-intercept, we look for the point where the y-value is 0 (i.e., where the graph touches the x-axis). When finding the y-intercept, the x-value is always 0, which is where the graph touches or crosses the y-axis.

Three graphical representations, each attempting to depict a relationship that may or may not represent a function. The leftmost graph shows a wavy, continuous blue line that starts from the left and oscillates up and down as it moves towards the right, ending with an arrowhead pointing to the right. This suggests a relationship where for each input value along the horizontal axis, there is a corresponding output value along the vertical axis. The central graph illustrates a blue curve resembling a sideways parabola opening to the left. In this case, some input values would correspond to two different output values. The rightmost graph shows an ellipse. In this representation, for many input values (except for the leftmost and rightmost points of the ellipse), there would be two corresponding output values (an upper and a lower point on the circle). Your Turn

Practice 1.2-3-1

Practice 1.2-3-2

Practice 1.2-3-3

Practice 1.2-3-4

Practice 1.2-3-5

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Math Mastery Manual Copyright © by Linglin (Niki) Liu is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book