"

1.3: Properties of functions

Learning Objectives

  1. Determine when a function is odd/even/neither from a graph or an equation.
  2. Determine when a function is increasing, decreasing, or constant from a graph.
  3. Identify local and absolute extrema (maximums or minimums) from a graph.

Determine a function from a graph

A function whose graph is symmetric about the y-axis is called an even function.

Same y value, but opposite x value.

A function with a graph that is symmetric about the origin is called an odd function.

Opposite y value and opposite x value.

Three graphs are shown, each representing a different type of function. The leftmost graph displays a blue curve that is symmetric about the vertical axis. It starts very close to the horizontal axis on both the left and right sides, then curves sharply upwards, moving away from the horizontal axis and extending upwards indefinitely, indicated by arrowheads The central graph shows a blue curve that starts in the first and fourth quadrant. The vertical axis and positive x-axis are an asymptote of the curve. The curve is symmetric with respect to x-axis. The rightmost graph also shows two separate blue curves. One curve is in the first quadrant, starting close to the vertical axis and extending upwards, curving to the right and approaching the horizontal axis. The other curve is in the third quadrant, starting close to the horizontal axis and extending downwards, curving to the left and approaching the vertical axis. The curves approach but do not touch the horizontal and vertical axes, indicating asymptotes. The curve is symmetric with respect to origin.

Master L3

A function can be neither even nor odd if it does not exhibit either symmetry.

For example, [latex]f\left(x\right)=2^x[/latex] is neither even nor odd. Also, the only function that is both even and odd is the constant function [latex]f(x)=0[/latex].

Example 1.3-1-1: Determine if it’s an even or odd function.

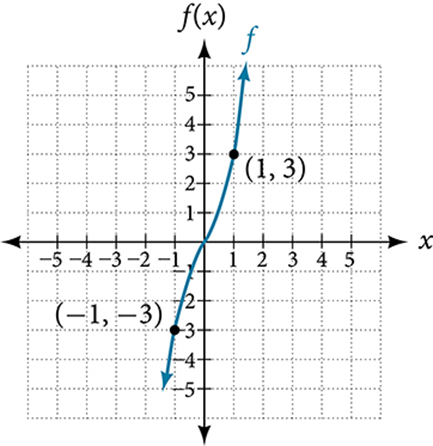
A graph of a function labeled f(x) on a Cartesian plane with labeled x and y axes, extending from -5 to 5 on the x-axis and -5 to 6 on the y-axis. The graph is a blue curve passing through the origin (0, 0). It also passes through the point (-1, -3) and the point (1, 3), which are explicitly labeled. The curve extends upwards and to the right in the first quadrant and downwards and to the left in the third quadrant, with arrowheads indicating that it continues beyond the visible portion. The graph exhibits symmetry about the origin.

Master L3 Key

Example 1.3-1-1: Determine if it’s an even or odd function.

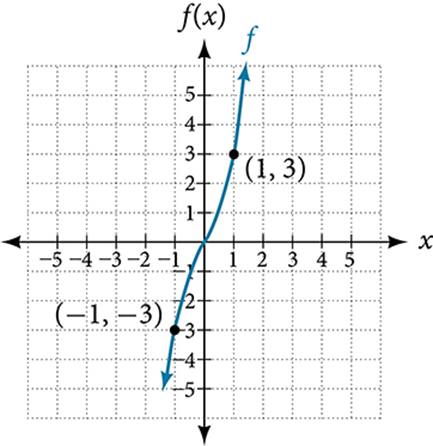
A graph of a function labeled f(x) on a Cartesian plane with labeled x and y axes, extending from -5 to 5 on the x-axis and -5 to 6 on the y-axis. The graph is a blue curve passing through the origin (0, 0). It also passes through the point (-1, -3) and the point (1, 3), which are explicitly labeled. The curve extends upwards and to the right in the first quadrant and downwards and to the left in the third quadrant, with arrowheads indicating that it continues beyond the visible portion. The graph exhibits symmetry about the origin.

Graph a is an Odd function. The graph is symmetric about the origin. For every point (x, y) on the graph, the corresponding point (−x, −y) is also on the graph. For example, (1, 3) is on the graph of f, and the corresponding point (−1, −3) is also on the graph.

Example 1.3-1-2: Determine if it’s an even or odd function.

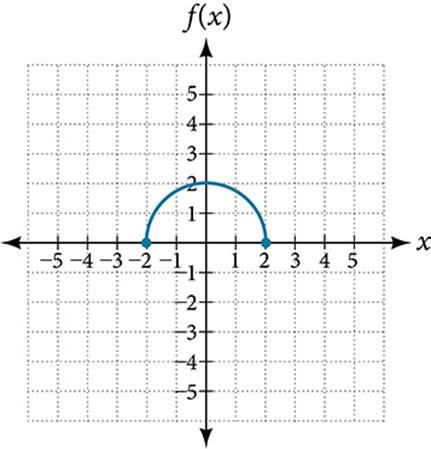
A graph of a function labeled f(x) on a Cartesian plane with labeled x and y axes, extending from -6 to 6 on the x-axis and -6 to 6 on the y-axis. The graph is a blue semi-circular arc positioned above the x-axis. The semicircle starts at a closed circle at the point (-2, 0), curves upwards with its highest point at (0, 2), and ends at a closed circle at the point (2, 0). This shape represents the upper half of a circle centered at the origin with a radius of 2.

Master L3 Key

Example 1.3-1-2: Determine if it’s an even or odd function.

A graph of a function labeled f(x) on a Cartesian plane with labeled x and y axes, extending from -6 to 6 on the x-axis and -6 to 6 on the y-axis. The graph is a blue semi-circular arc positioned above the x-axis. The semicircle starts at a closed circle at the point (-2, 0), curves upwards with its highest point at (0, 2), and ends at a closed circle at the point (2, 0). This shape represents the upper half of a circle centered at the origin with a radius of 2.

Graph a is an Even function. The graph is symmetric about the y-axis. For every point (x, y) on the graph, the corresponding point (−x, y) is also on the graph. For example, (-2, 0) is on the graph of f, and the corresponding point (2, 0) is also on the graph.

IXL | Graph points on a coordinate plane | 5th grade math Your Turn

Practice 1.3-1-1

Determine a function from equation

Given the formula for a function, determine if the function is even, odd, or neither.

Determine whether the function satisfies [latex]f\left(x\right)=f\left(-x\right)[/latex].

If it does, it is even.

Determine whether the function satisfies [latex]f\left(x\right)=-f\left(-x\right)[/latex].

If it does, it is odd.

If the function does not satisfy either rule, it is neither even nor odd.

Example 1.3-1-3: Determine if it’s an even or odd function algebraically.

[latex]f\left(x\right)=3x^2+7[/latex]

Master L3 Key

Example 1.3-1-3: Determine if it’s an even or odd function algebraically.

[latex]f\left(x\right)=3x^2+7[/latex]

Step1: use [latex]-x[/latex]substitue the [latex]x[/latex]

[latex]f\left(-x\right)=3\left(-x\right)^2+7[/latex]

Step 2: simplify the function

[latex]f\left(-x\right)=3x^2+7[/latex]

Step 3: compare [latex]f(-x)[/latex] with [latex]f(x)[/latex], if [latex]f(x)=f(-x)[/latex] even, if [latex]f(x)=-f(-x)[/latex] odd, other than that, netiher.

Since in this question, [latex]f(x)=f(-x)[/latex], thus it is an even function.

Another way to analyze symmetry is by comparing with [latex]f(x)[/latex] with [latex]f(-x)[/latex] or [latex]-f(-x)[/latex]

After finding [latex]f(-x)[/latex], examine the expression and compare it with the original function [latex]f(x)[/latex]:

  • If all terms are the same, the function is even.
  • If all terms are the opposite (i.e., the signs are reversed), the function is odd.
  • If the expression contains a mix of same and opposite terms, the function is neither even nor odd.
Character

In this question [latex]f\left(x\right)=3x^2+7[/latex]

And we found [latex]f\left(-x\right)=3x^2+7[/latex]

Since both [latex]3x^2[/latex] and +7 terms are the same, thus it is an even function.

Example 1.3-1-4: Determine if it’s an even or odd function algebraically.

[latex]f\left(x\right)=3x^2+2x[/latex]

Master L3 Key

Example 1.3-1-4: Determine if it’s an even or odd function algebraically.

[latex]f\left(x\right)=3x^2+2x[/latex]

Step1: use [latex]-x[/latex] substitue the [latex]x[/latex]

[latex]f\left(-x\right)=3\left(-x\right)^2+2\left(-x\right)[/latex]

Step 2: simplify the function

[latex]f\left(-x\right)=3x^2-2x[/latex]

Step 3: compare [latex]f(-x)[/latex] with [latex]f(x)[/latex], if [latex]f(x)=f(-x)[/latex]even, if [latex]f(x)=-f(-x)[/latex] odd, other than that, netiher. In this question, [latex]f(x)≠f(-x)[/latex], [latex]f(x)≠-f(-x)[/latex] thus it is it neither.

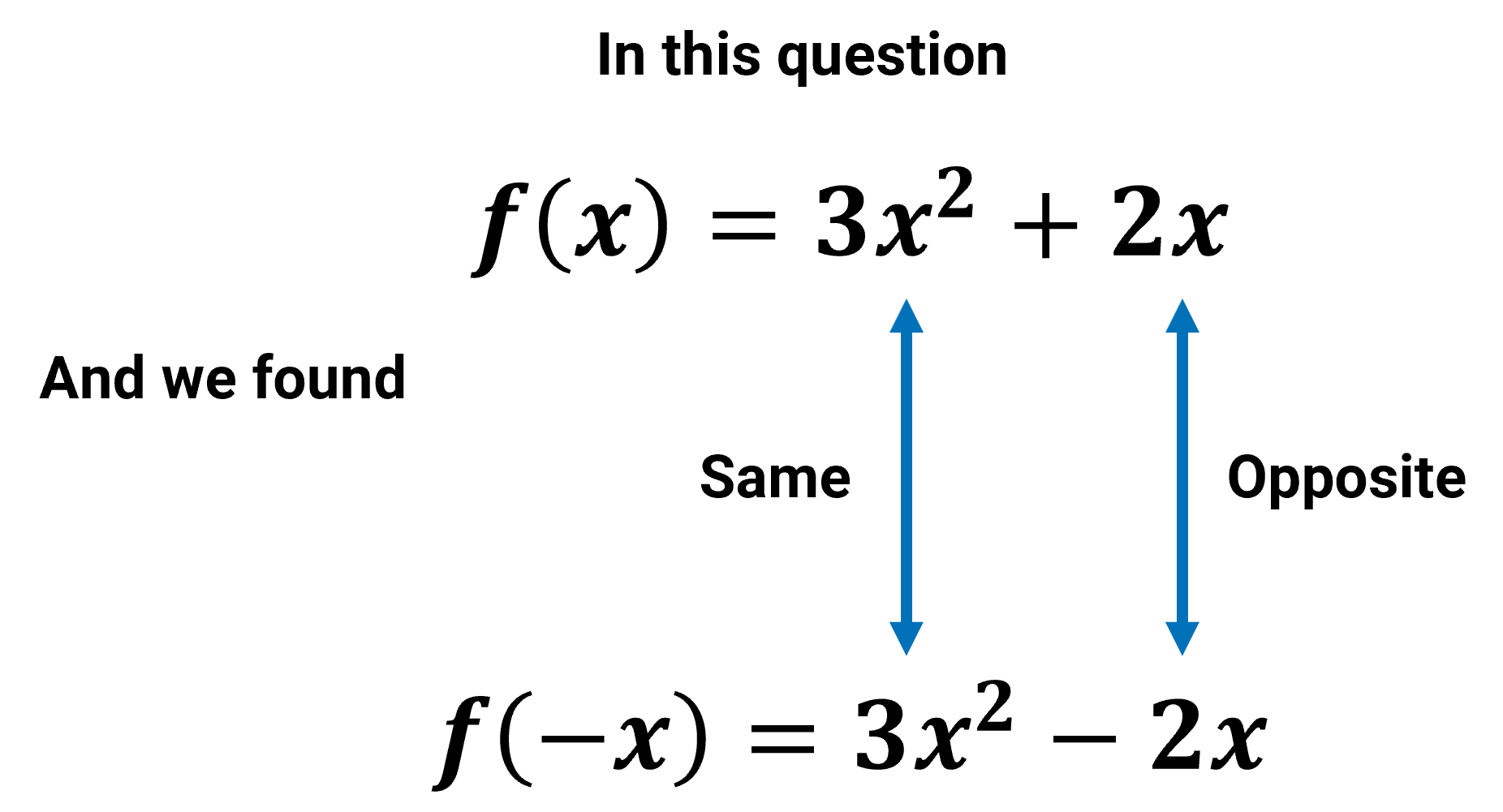
In this equation f(x) equals 3 x squared plus 2x and we found that f(-x) equals 3 x squared minus 2x, where coefficient of x squared remains same but the coefficient of x is opposite sign in f(-x).

Since both [latex]3x^2[/latex] term is the same, however the second term [latex]+2x[/latex] and [latex]-2x[/latex] are opposite, thus it is neither.

Example 1.3-1-5: Determine if it’s an even or odd function algebraically.

[latex]f\left(x\right)=5x^3+x[/latex]

Master L3 Key

Example 1.3-1-5: Determine if it’s an even or odd function algebraically.

[latex]f\left(x\right)=5x^3+x[/latex]

Step1: use [latex]-x[/latex] substitue the [latex]x[/latex]

[latex]f\left(-x\right)=5\left(-x\right)^3+\left(-x\right)[/latex]

Step 2: simplify the function

[latex]f\left(-x\right)=-5x^3-x[/latex]

Step 3: compare [latex]f(-x)[/latex] with [latex]f(x)[/latex], if [latex]f(x)=f(-x)[/latex] even, if [latex]f(x)=-f(-x)[/latex] odd, other than that, netiher. In this question, [latex]f(x)≠f(-x)[/latex], but [latex]f(x)=-f(-x)[/latex] thus it is an odd function.

In this question "f of x equals 5x cubed plus x". Below this, the text "And we found" is shown. Between the two equations, two blue vertical arrows point downwards. Above the left arrow, the word "Opposite" is written. Above the right arrow, the word "Opposite" is also written. Below the arrows, the equation "f of minus x equals minus 5x cubed minus x" is displayed.

Since both terms are opposite, thus it is odd.

IXL | Graph points on a coordinate plane | 5th grade math Your Turn

Practice 1.3-1-2

Determine increasing, decreasing, or constant from a graph.

A function [latex]f[/latex] is increasing function on an open interval [latex]I[/latex] if[latex]b>a[/latex] and [latex]f(b)>f(a)[/latex].

A function [latex]f[/latex] is decreasing function on an open interval [latex]I[/latex] if [latex]b>a[/latex] and [latex]f(b)A function [latex]f[/latex] is constant function on an open interval [latex]I[/latex] if [latex]b>a[/latex] and [latex]f(b)=f(a)[/latex].

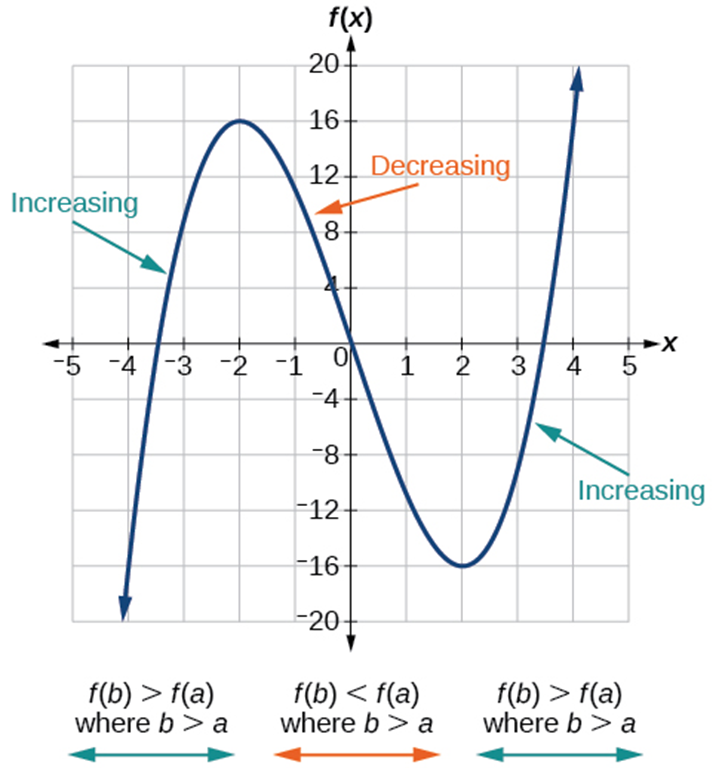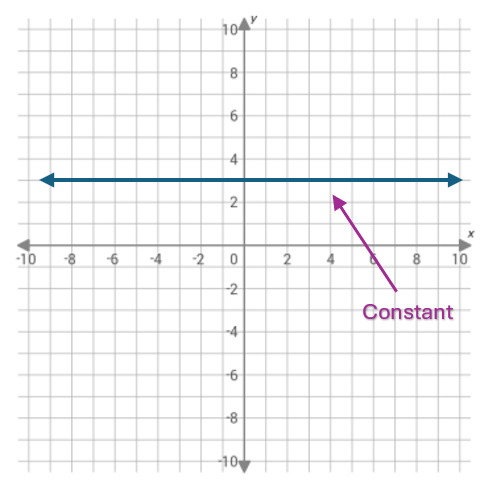
Graph of a polynomial that shows the increasing and decreasing intervals and local maximum and minimum. Graph of a constant function which is parallel to horizontal axis.

Constant function [latex]b>a[/latex] where [latex]f(b)=f(a)[/latex].

Example 1.3-2-1:

Determine the interval(s) on which the function is increasing, decreasing and constant. Use interval notation, if you can’t find it, put N/A.

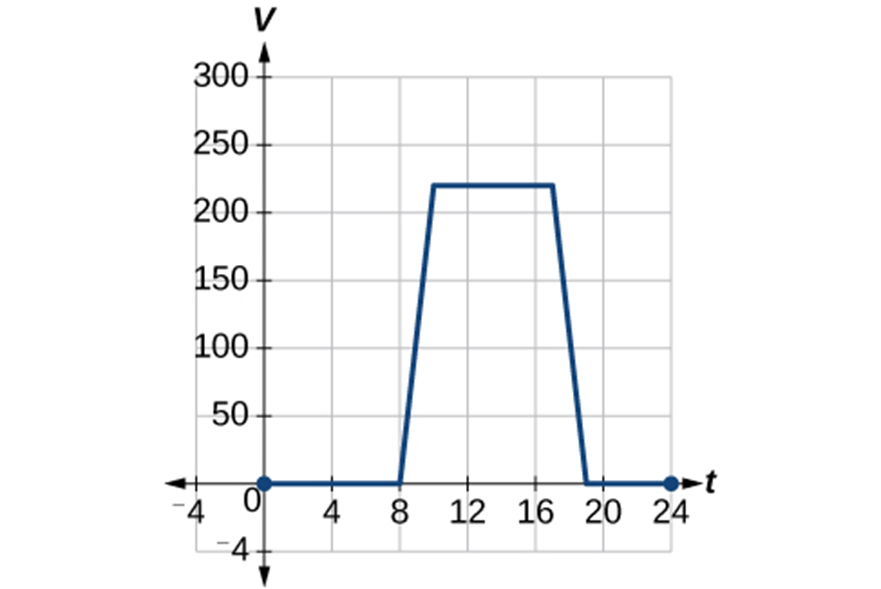
A velocity versus time graph for an elevator is shown on a Cartesian plane. The horizontal axis represents time (t) in seconds, ranging from -4 to 24. The vertical axis represents velocity (v) ranging from -4 to 300. The graph starts at a velocity of 0 at time t=0. The v value remains 0 until time t=8 seconds. From t=8 seconds to t=10 seconds, the v value increases linearly from 0 to approximately 220 From t=10 seconds to approximately t=17 seconds, the v value remains constant approximately at 220. From t=17 seconds to t=19 seconds, the v value decreases linearly from approximately 220 to 0 The v value remains 0 from t=19 seconds to t=24 seconds.

Master L3 Key

Example 1.3-2-1: Determine the interval(s) on which the function is increasing, decreasing and constant. Use interval notation, if you can’t find it, put N/A.

A graph of a function P(t) versus time t is shown on a Cartesian plane. The horizontal axis represents time (t), ranging from -1 to 7. The vertical axis represents the value of the function P(t), ranging from -1 to 7. The graph starts at a point (0, 1). From t=0 to t=3, the function increases non-linearly, curving upwards and reaching a maximum value of 3 at t=3. From t=3 to t=6, the function decreases linearly from 3 to 2. This indicates a constant rate of decrease over this time interval. From t=6 to t=7, the function decreases linearly from 2 to 0. This indicates a steeper constant rate of decrease compared to the previous interval.

Increasing: (0,3)

Decreasing: (3,7)

Constant: N/A

Note: Do not use brackets. Even though this graph shows a closed point, when we determine where a function is increasing, decreasing, or constant, we only consider open intervals. Therefore, use parentheses only.

IXL | Graph points on a coordinate plane | 5th grade math Your Turn

Practice 1.3-2-1

Identify local and absolute maximums and minimums

Term Definition Analogy
Local Maximum A function has a local maximum at a point b if the value at b is higher than all nearby points. Hill
Local Minimum A function has a local minimum at a point b if the value at b is lower than all nearby points. Valley
Absolute Maximum A function has an absolute maximum at [latex]x = c[/latex] if [latex]f(c)[/latex] is the greatest value the function ever reaches. This means [latex]f(c) ≥ f(x)[/latex] for every x in the domain. The Highest Point
Absolute Minimum A function has an absolute minimum at [latex]x = d[/latex] if [latex]f(d)[/latex] is the smallest value the function ever reaches. This means [latex]f(d) ≤ f(x)[/latex] for every x in the domain. The Lowest Point

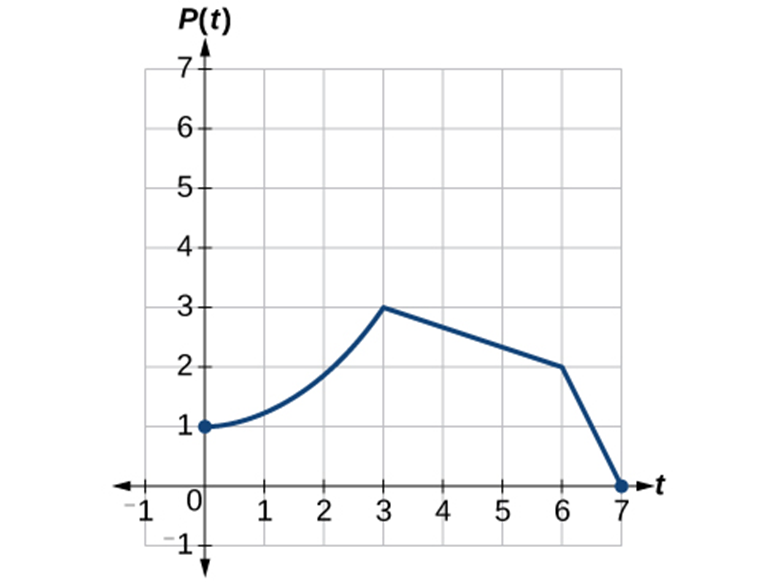
Example 1.3-3-1: Use the graphed function to answer the following questions.

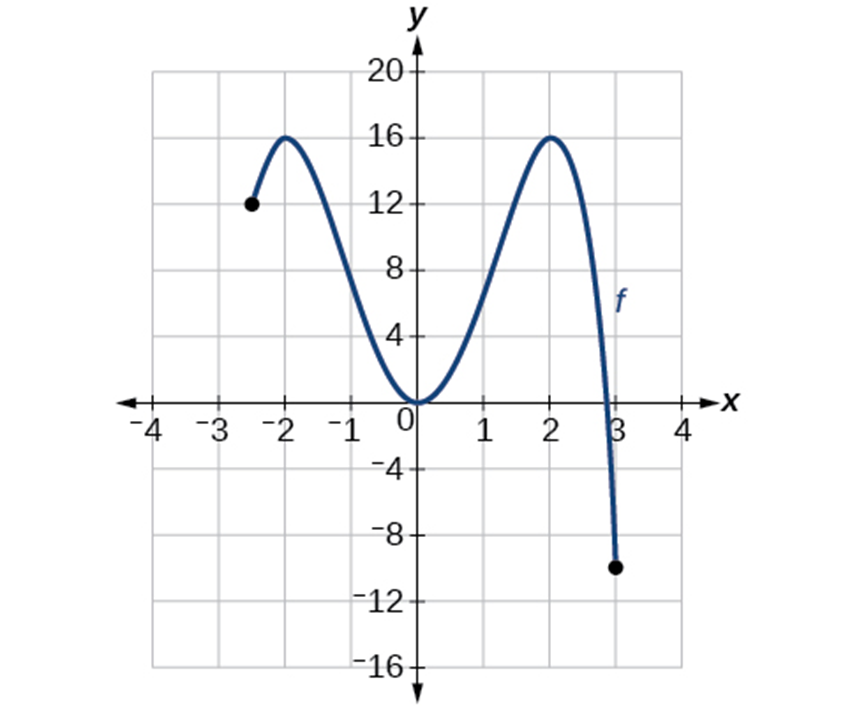
A graph of a function labeled "f" is plotted on a coordinate plane. The x-axis ranges from -4 to 4, and the y-axis ranges from -16 to 20. The function starts at approximately (−2.5,12) with a solid dot, reaches to a local maxima at (-2, 16) decreases to a local minimum at (0,0), increases to a local maximum at approximately (2,16), and then decreases sharply, ending at (3,−10) with a solid dot.

  1. Use the graph find local maximum.
  2. Use the graph find local minimum.
  3. Use the graph find absolute maximum.
  4. Use the graph find absolute minimum.

Master L3 Key

Example 1.3-3-1: Use the graphed function to answer the following questions.

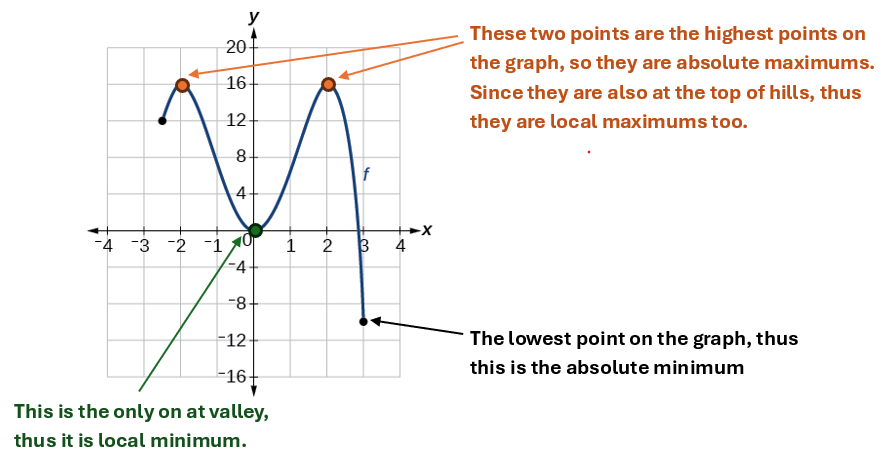
A graph of a function labeled "f" is plotted on a coordinate plane. The x-axis ranges from -4 to 4, and the y-axis ranges from -16 to 20. The function, depicted as a dark blue curve, starts at a solid dot approximately at the coordinates (-2.5, 12). It increases to a local maximum at the point (-2, 16), then decreases to a local minimum at the origin (0, 0). Following this, the function increases again to another local maximum at approximately (2, 16), before sharply decreasing and ending at a solid dot at the coordinates (3, -10). Annotations on the graph point to the local minimum at (0,0) labeling it as 'This is the only on at valley, thus it is local minimum.', and to the two local maxima at (-2, 16) and (2, 16) stating 'These two points are the highest points on the graph, so they are absolute maximums. Since they are also at the top of hills, thus they are local maximums too.'. Another annotation points to the endpoint at (3, -10) and describes it as 'The lowest point on the graph, thus this is the absolute minimum'.

  1. Local maximum: 16
  2. Local minimum: 0
  3. Absolute maximum: 16
  4. Absolute minimum: -10

Example 1.3-3-2: Use the graphed function to answer the following questions.

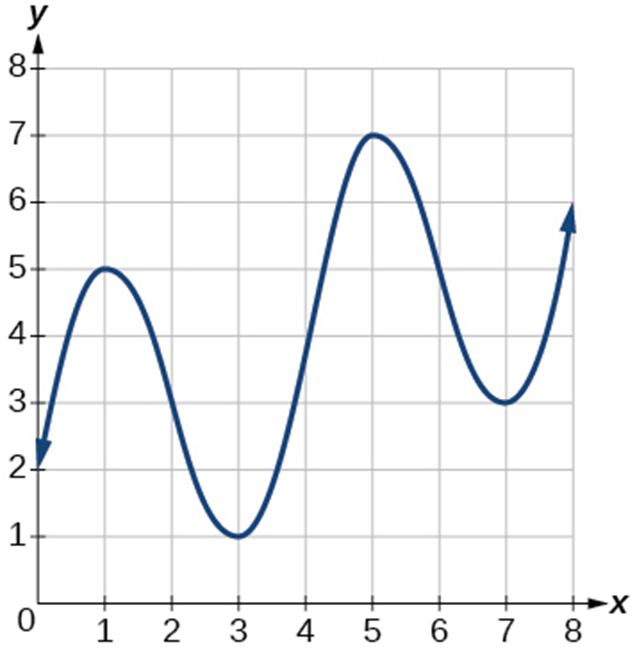
A graph of a periodic function is shown on a Cartesian coordinate system. The x-axis ranges from 0 to 8, and the y-axis ranges from 0 to 8. The function, depicted by a dark blue curve, starts at approximately (0, 2.5) and increases to a local maximum at (1, 5). It then decreases to a local minimum at approximately (3, 1), followed by an increase to a local maximum at approximately (5, 7). The function then decreases to a local minimum at approximately (7, 3) and appears to continue increasing beyond x=8, indicated by an arrow pointing upwards. The graph suggests a wave-like pattern.

  1. Use the graph find local maximum.
  2. Use the graph find local minimum.
  3. Use the graph find absolute maximum.
  4. Use the graph find absolute minimum.

Master L3 Key

Example 1.3-3-2: Use the graphed function to answer the following questions.

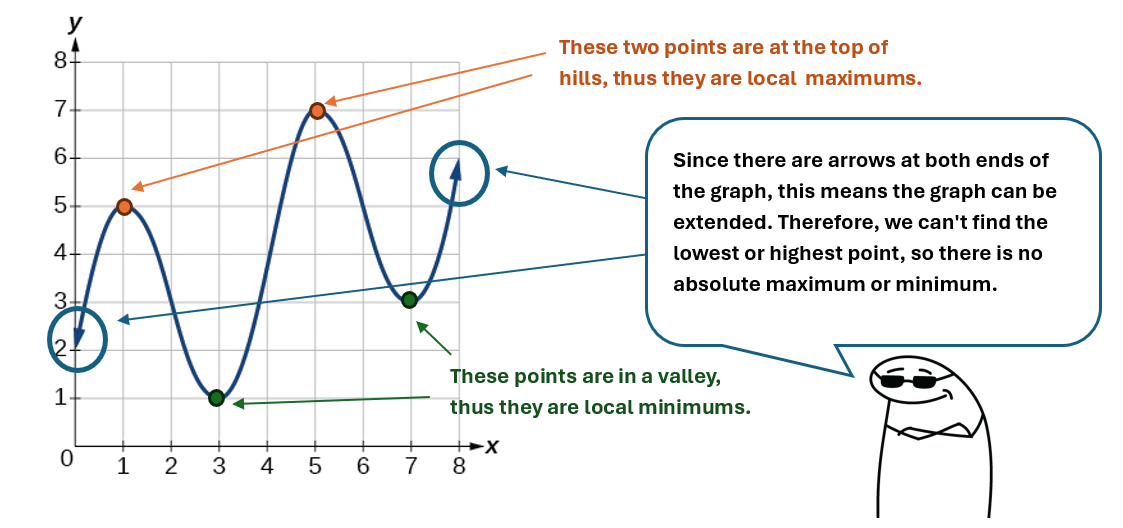
A graph of a continuous function is shown on a Cartesian coordinate system. The x-axis ranges from 0 to 8, and the y-axis ranges from 0 to 8. The function, depicted by a dark blue curve with arrows at both ends indicating it extends beyond the visible range, exhibits several local extrema. There are local maxima at approximately x=1 and x=5, marked with orange dots and labeled 'These two points are at the top of hills, thus they are local maximums.' Local minima are present at approximately x=3 and x=7, marked with green dots and labeled 'These points are in a valley, thus they are local minimums.' A speech bubble originating from a cartoon figure in the bottom right corner states, 'Since there are arrows at both ends of the graph, this means the graph can be extended. Therefore, we can't find the lowest or highest point, so there is no absolute maximum or minimum.'"

  1. Local maximum: 5, 7
  2. Local minimum: 1, 3
  3. Absolute maximum: N/A
  4. Absolute minimum: N/A

IXL | Graph points on a coordinate plane | 5th grade math Your Turn

Practice 1.3-3-1

Practice 1.3-3-2

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Math Mastery Manual Copyright © by Linglin (Niki) Liu is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book