"

1.5: Graphing techniques: transformations; solving radical equations

Learning Objectives

  1. Graph functions using vertical and horizontal shifts.
  2. Graph functions using compressions and stretches.
  3. Graph functions using reflections about the axes.
  4. Find the equation of function from the transformations.

Graphing Functions Using Vertical And Horizontal Shifts

Vertical Shift

Given a function [latex]f\left(x\right)[/latex], a new function [latex]g\left(x\right)=f\left(x\right)+k[/latex], where [latex]k[/latex] is a constant, is a vertical shift of the function [latex]f\left(x\right)[/latex]. All the output values change by [latex]k[/latex] units. If [latex]k[/latex] is positive, the graph will shift up. If [latex]k[/latex] is negative, the graph will shift down.

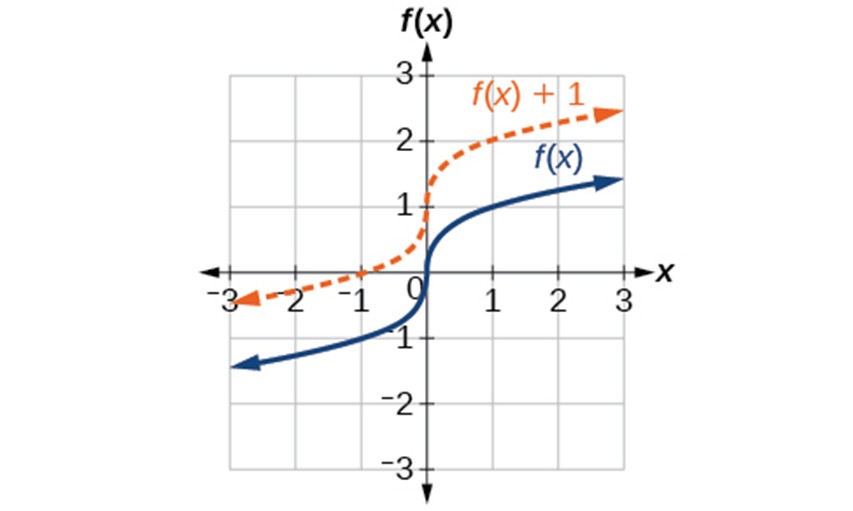
A graph on a Cartesian coordinate system with the x-axis ranging from -3 to 3 and the y-axis ranging from -3 to 3. Two curves are plotted. A solid blue curve, labeled 'f(x)', starts in the third quadrant, curves through the origin (0, 0), and extends into the first quadrant with an arrow indicating it continues to increase. A dashed orange curve, labeled 'f(x) + 1', is vertically shifted upwards by one unit compared to f(x). It starts in the third quadrant, passes through (0, 1), and extends into the first quadrant with an arrow, indicating it also continues to increase.

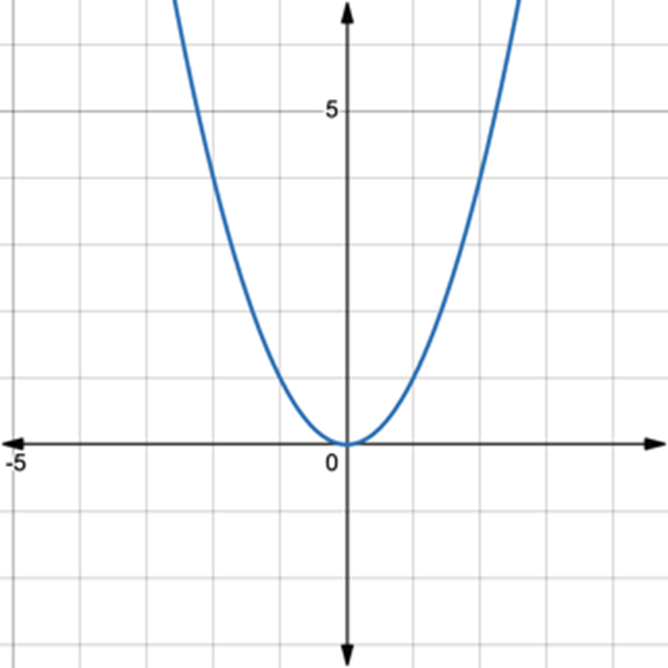
Example 1.5-1-1: Given the graph [latex]f\left(x\right)=x^2[/latex], graph the transformed function: [latex]f\left(x\right)=x^2+2[/latex].

[latex]f\left(x\right)=x^2[/latex]

Master L3 Key

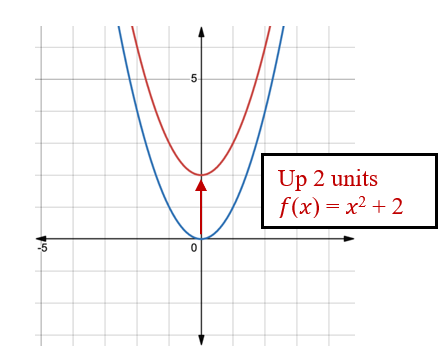
Example 1.5-1-1: Given the graph [latex]f\left(x\right)=x^2[/latex], graph the transformed function: [latex]f\left(x\right)=x^2+2[/latex]

Graph of f(x) equals x squared.

[latex]f\left(x\right)=x^2[/latex]

If the whole function [latex]f\left(x\right)[/latex] changes, then up or down. [latex]k[/latex] is 2 which is positive, the graph will shift up 2 units.

Graphs of f(x) equals x squared in blue and graph of f(x)= x squared plus 2 in red.

Horizontal Shift

Given a function [latex]f[/latex],a new function [latex]g\left(x\right)=f\left(x-h\right)[/latex], where [latex]h[/latex] is a constant, is a horizontal shift of the function [latex]f[/latex]. If [latex]h[/latex] is positive, the graph will shift right. If [latex]h[/latex] is negative, the graph will shift left.

A graph on a Cartesian coordinate system with the x-axis ranging from -3 to 3 and the y-axis ranging from -3 to 3. Two curves are plotted. A solid blue curve, labeled 'f(x)', starts in the third quadrant, curves through the origin (0, 0), and extends into the first quadrant with an arrow indicating it continues to increase. A dashed orange curve, labeled 'f(x) + 1', is vertically shifted upwards by one unit compared to f(x). It starts in the third quadrant, passes through (0, 1), and extends into the first quadrant with an arrow, indicating it also continues to increase.

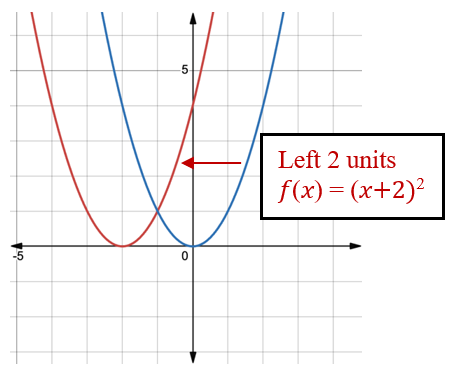
Example 1.5-1-2: Given the graph [latex]f\left(x\right)=x^2[/latex], graph the transformed function: [latex]f\left(x\right)=\left(x+2\right)^2[/latex].

Graph of f(x) equals x squared.

Master L3 Key

Example 1.5-1-2: Given the graph [latex]f\left(x\right)=x^2[/latex], graph the transformed function: [latex]f\left(x\right)=\left(x+2\right)^2[/latex]

[latex]f\left(x\right)=x^2[/latex]

[latex]f\left(x\right)=\left(x+2\right)^2[/latex]

The change relates to x, and since function f\left(x\right)=\left(x-\left(-2\right)\right)^2 where [latex]h[/latex] is -2, [latex]h[/latex] is negative, the graph will shift left 2 units.

Graphs of f(x) equals x squared in blue and graph of f(x)= x plus 2 squared in red.

Graphing Functions Using Compressions And Stretches

Vertical Stretches and Compressions

Given a function [latex]f\left(x\right)[/latex], a new function [latex]g\left(x\right)=af\left(x\right)[/latex], where a is a constant, is a vertical stretch or vertical compression of the function [latex]f\left(x\right)[/latex].

  • If [latex]a>1[/latex], then the graph will be stretched.
  • If 0 < a < 1, then the graph will be compressed.
  • If [latex]a<0[/latex], then there will be combination of a vertical stretch or compression with a vertical reflection.

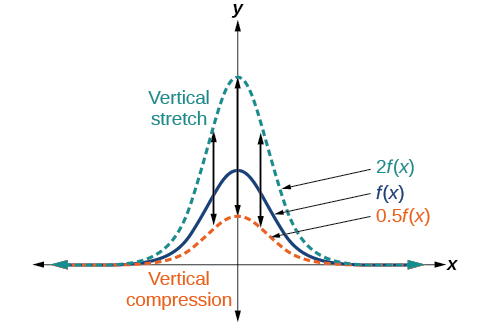
A graph illustrating vertical stretches and compressions of a function. The x-axis and y-axis intersect at the origin (0, 0). Three curves are plotted, all symmetric about the y-axis and centered at x=0. A solid blue curve represents the original function, labeled 'f(x)'. A dashed teal curve, labeled '2f(x)', is vertically stretched compared to f(x), appearing taller and narrower. Vertical arrows point from the blue curve to the teal curve, indicating the vertical stretch. A dashed orange curve, labeled '0.5f(x)', is vertically compressed compared to f(x), appearing shorter and wider. The x-axis extends with arrows in both directions, and the y-axis extends upwards. Labels 'Vertical stretch' in teal and 'Vertical compression' in orange are placed near the respective transformed curves to further clarify the transformations.

Steps:

Given a function, graph its vertical stretch.

  1. Identify the value of [latex]a[/latex].
  2. Multiply all range values by [latex]a[/latex].
  3. If [latex]a>1[/latex], the graph is stretched by a factor of a.

    If 0 < a < 1, the graph is compressed by a factor of a.

    If [latex]a<0[/latex], the graph is either stretched or compressed and also reflected about the x-axis.

Horizontal Stretches and Compressions

Given a function [latex]f\left(x\right)[/latex], a new function [latex]g\left(x\right)=f\left(bx\right)[/latex], where [latex]b[/latex] is a constant, is a horizontal stretch or horizontal compression of the function [latex]f\left(x\right)[/latex].

  • If [latex]b>1[/latex], then the graph will be compressed by [latex]b[/latex].
  • If 0 < b < 1, then the graph will be stretched by [latex]\frac1b[/latex].
  • If [latex]b<0[/latex], then there will be combination of a horizontal stretch or compression with a horizontal reflection.

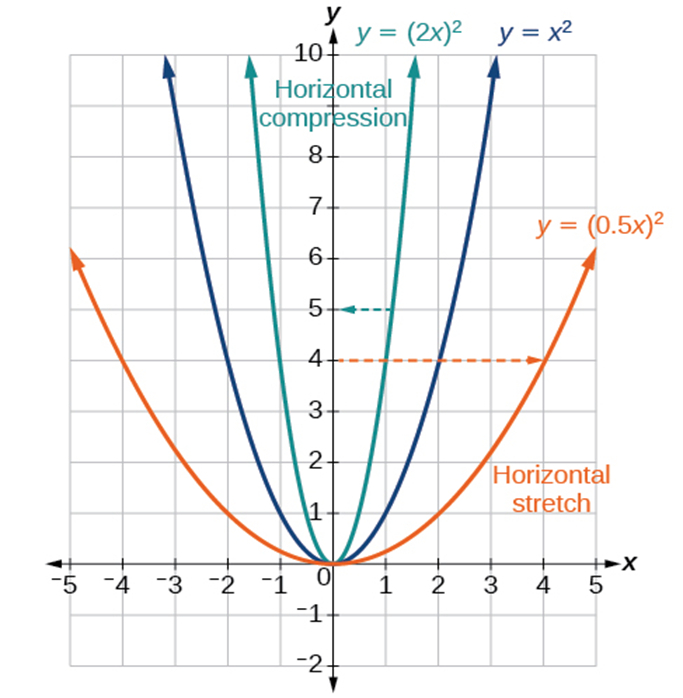
A graph illustrating horizontal stretches and compressions of a parabola. The x-axis ranges from -5 to 5, and the y-axis ranges from -2 to 10, with grid lines at integer values. Three parabolas are plotted, all opening upwards with their vertex at the origin (0, 0). A dark blue parabola represents the function y = x squared. A teal parabola, labeled 'y = (2x) squared', is horizontally compressed compared to y = x squared, appearing narrower. An orange parabola, labeled 'y = (0.5x) squared', is horizontally stretched compared to y = x², appearing wider.

Steps:

Given a description of a function, sketch a horizontal compression or stretch.

  1. Write a formula to represent the function.
  2. Set [latex]g\left(x\right)=f\left(bx\right)[/latex] where [latex]b >1[/latex] for a compression or 0 < b < 1 for a stretch.

Example 1.5-2-1: Given the graph, graph the transformed function

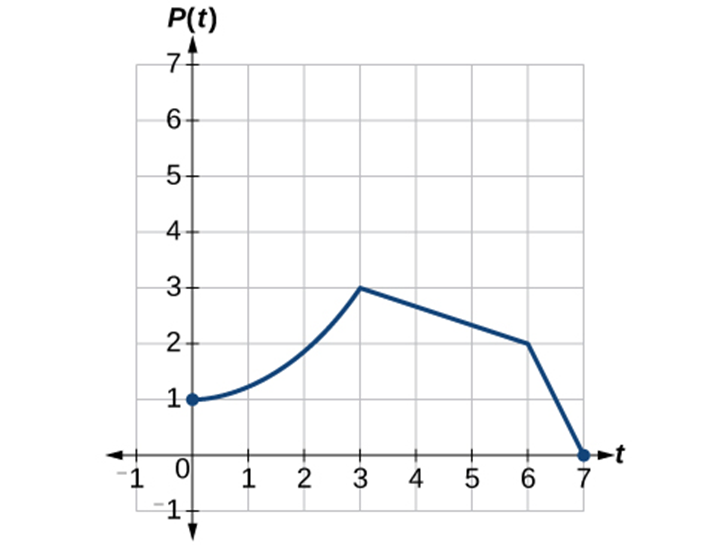
A graph of a function P(t) is shown on a Cartesian coordinate system. The horizontal axis is labeled 't' and ranges from -1 to 7, representing time. The vertical axis is labeled 'P(t)' and ranges from -1 to 7, representing some quantity P as a function of time. The graph starts at a solid blue circle at the point (0, 1). It then increases with a slight upward curve to a peak at the point (3, 3). From there, the graph decreases linearly to the point (6, 2). Finally, it decreases sharply and linearly to a solid blue circle at the point (7, 0).

Master L3 Key

Example 1.5-2-1: Given the graph, graph the transformed function

If we choose four reference points, (0, 1), (3, 3), (6, 2) and (7, 0) … …

[latex]\left(7,\;0\right)\rightarrow\left(7,\;0\right)[/latex]

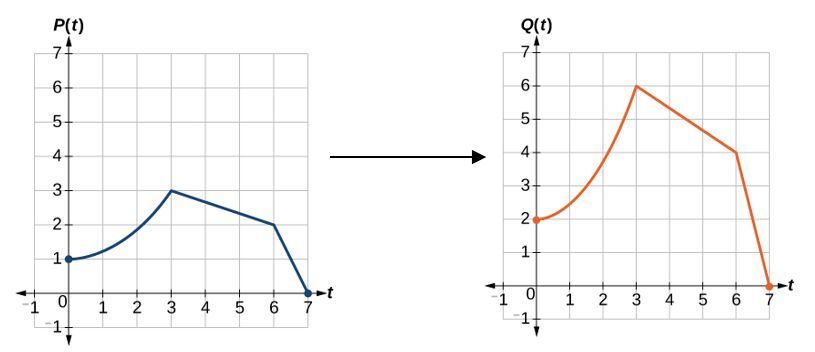
The left graph shows a function P(t) plotted against time t. The t-axis ranges from -1 to 7, and the P(t)-axis ranges from -1 to 7, with grid lines at integer values. The function starts at (0, 1), increases to a peak at (3, 3), decreases to (6, 2), and then drops to (7, 0). The right graph shows a function Q(t) plotted against time t, using the same axis ranges and grid lines as the left graph. The function Q(t) is depicted by an orange line. It starts at (0, 2), increases to a peak at (3, 6), decreases to (6, 4), and then drops to (7, 0).

Graphing Functions Using Reflections About the Axes

Reflections

Given a function [latex]f\left(x\right)[/latex], a new function [latex]g\left(x\right)=-f\left(x\right)[/latex] is a vertical reflection of the function [latex]f\left(x\right)[/latex], sometimes called a reflection about (or over, or through) the x-axis.

Given a function [latex]f\left(x\right)[/latex], a new function [latex]g\left(x\right)=f\left(-x\right)[/latex] is a horizontal reflection of the function [latex]f\left(x\right)[/latex], sometimes called a reflection about the y-axis.

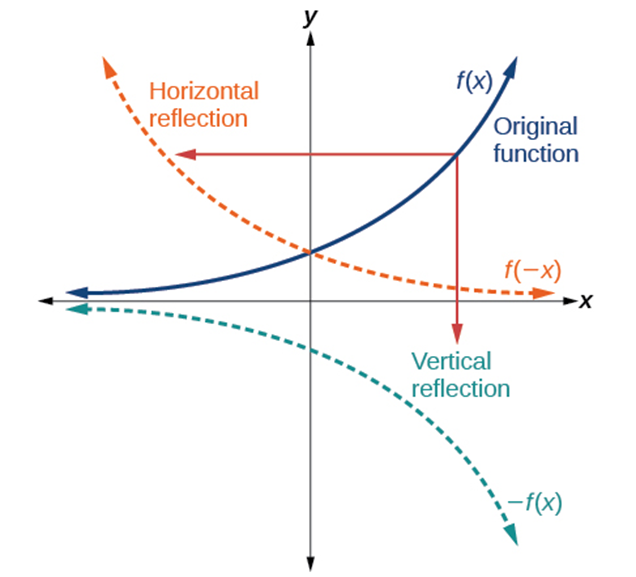
A solid blue curve, labeled 'f(x) Original function', starts in the second quadrant and extends into the first quadrant, increasing exponentially. A dashed orange curve, labeled 'f(-x) Horizontal reflection', is a reflection of f(x) across the y-axis. It starts in the first quadrant and extends into the second quadrant, increasing exponentially as x becomes more negative. A horizontal red arrow connects a point on f(x) in the first quadrant to its reflected point on f(-x) in the second quadrant, indicating the horizontal reflection. The label 'Horizontal reflection' in orange is placed above this curve. A dashed teal curve, labeled '-f(x) Vertical reflection', is a reflection of f(x) across the x-axis. It starts in the third quadrant and extends into the fourth quadrant, decreasing exponentially. A vertical red arrow connects a point on f(x) in the first quadrant to its reflected point on -f(x) in the fourth quadrant, indicating the vertical reflection.

Steps:

Given a function, reflect the graph both vertically and horizontally.

  1. Multiply all outputs by –1 for a vertical reflection. The new graph is a reflection of the original graph about the x-axis.
  2. Multiply all inputs by –1 for a horizontal reflection. The new graph is a reflection of the original graph about the y-axis.

Example 1.5-3-1: Given the graph [latex]s\left(t\right)=\sqrt t[/latex], graph the transformed function [latex]v\left(t\right)=-\sqrt t[/latex]

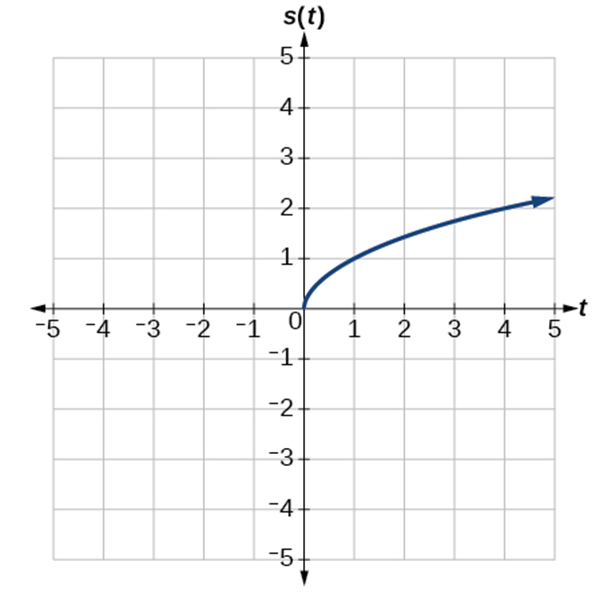
Graph of square root of t.

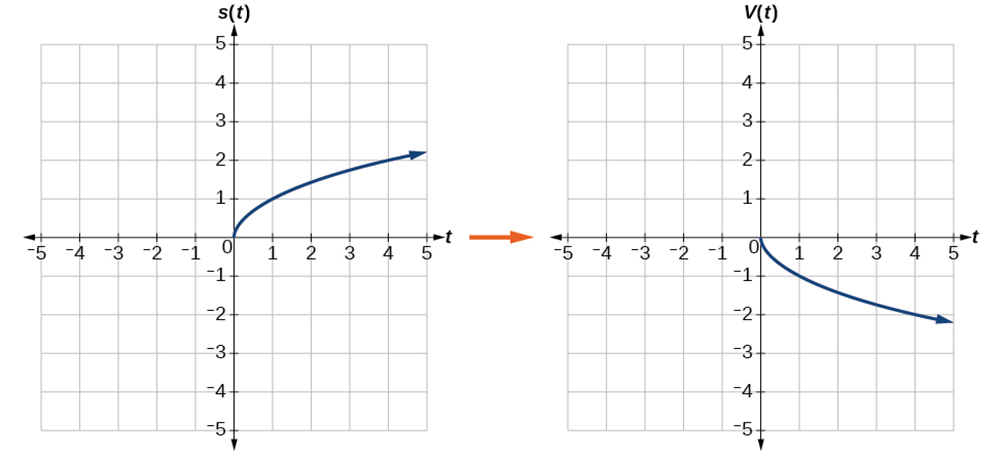
Master L3 Key

Example 1.5-3-1: Given the graph [latex]s\left(t\right)=\sqrt t[/latex], graph the transformed function [latex]v\left(t\right)=-\sqrt t[/latex]

Because each output value is the opposite of the original output value, we can write

[latex]V\left(t\right)=-s\left(t\right)\;or\;V\left(t\right)=-\sqrt t[/latex]

Graph of square root of t in the left and graph of minus square root of t in the right.

IXL | Graph points on a coordinate plane | 5th grade math Your Turn

Practice 1.5-3-1

Example 1.5-4-1: Identify combined vertical and horizontal shift and write the transformed function.

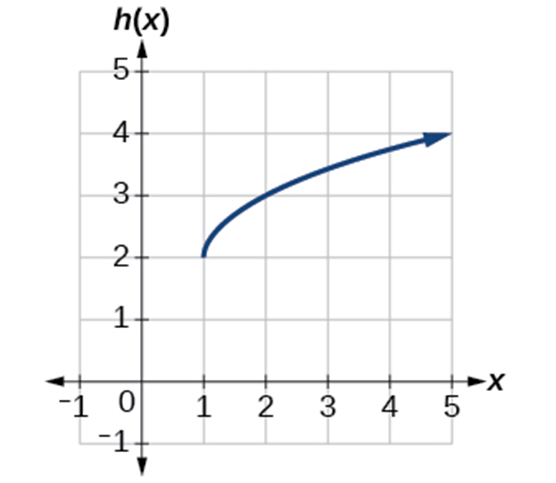
A graph of a function h(x) is shown on a Cartesian coordinate system. The horizontal axis is labeled 'x' and ranges from -1 to 5. The vertical axis is labeled 'h(x)' and ranges from -1 to 5, with grid lines at integer values. A dark blue curve starts at the point (1, 2) and increases with a decreasing rate, extending into the first quadrant. At x=2, h(x) is approximately 3; at x=5, h(x) is approximately 4. An arrow at the end of the curve indicates that it continues to increase slowly as x increases.

Master L3 Key

Example 1.5-4-1: Identify combined vertical and horizontal shift and write the transformed function.

A graph of a function h(x) is shown on a Cartesian coordinate system. The horizontal axis is labeled 'x' and ranges from -1 to 5. The vertical axis is labeled 'h(x)' and ranges from -1 to 5, with grid lines at integer values. A dark blue curve starts at the point (1, 2) and increases with a decreasing rate, extending into the first quadrant. At x=2, h(x) is approximately 3; at x=5, h(x) is approximately 4. An arrow at the end of the curve indicates that it continues to increase slowly as x increases.

Based on the given graph, we can tell that it represents a square root function. First, we need to identify the parent graph—the original graph. Then, by comparing it with the transformed graph, we can determine the movement.

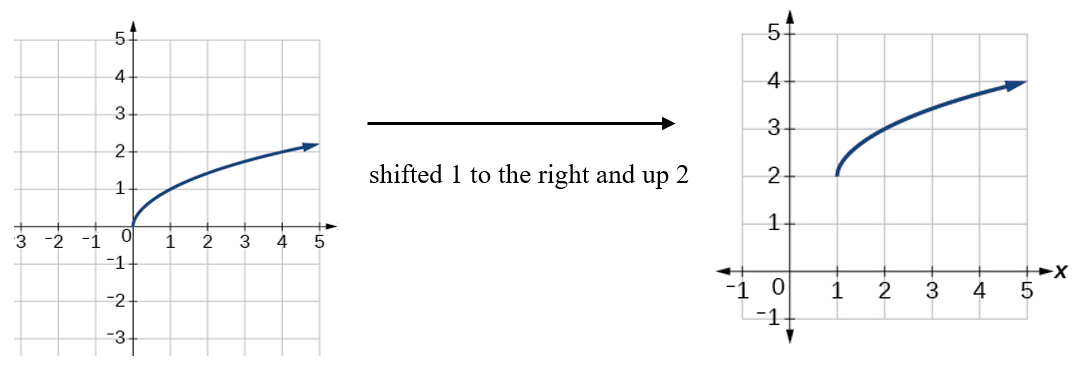
Two graphs are shown side-by-side, connected by a horizontal black arrow pointing from left to right, indicating a transformation. The left graph shows a function plotted on a Cartesian coordinate system with the x-axis ranging from -3 to 5 and the y-axis ranging from -3 to 5. A dark blue curve starts at the origin (0, 0) extending into the first quadrant with an arrow ending at approximately (4, 2). This represents a square root function. The right graph shows another function plotted on a Cartesian coordinate system with the x-axis ranging from -1 to 5 and the y-axis ranging from -1 to 5. A dark blue curve starts at the point (1, 2) extending into the first quadrant with an arrow ending at approximately (5, 4). This curve has the same shape as the one on the left but is shifted. Below the arrow connecting the two graphs, the text 'shifted 1 to the right and up 2' describes the transformation applied to the function in the left graph to obtain the function in the right graph.

Using the formula for the square root function, we can write

[latex]h\left(x\right)=\sqrt x\xrightarrow[{shifted\;1\;unit\;to\;the\;right\;}]{}\sqrt{x-1}\xrightarrow[{up\;2\;units\;}]{}\sqrt{x-1}+2[/latex]

Answer: [latex]h\left(x\right)=\sqrt{x-1}+2[/latex]

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Math Mastery Manual Copyright © by Linglin (Niki) Liu is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book