"

2.1: Quadratic Functions and Their Zeros

Learning Objectives

  1. Find the zeros of a quadratic function.
  2. Solve equations using the AC (Factoring) method.
  3. Solve equations using the Square Root method.
  4. Solve equations using the Quadratic Formula method.

Find the Zeros of a Quadratic Function

A quadratic function is any function of the form

[latex]f\left(x\right)=ax^2+bx+c[/latex]

where [latex]a, b,[/latex] and [latex]c[/latex] are real numbers and [latex]a≠0[/latex].

A quadratic equation is an equation equivalent to one in the form function of the form:

[latex]ax^2+bx+c=0[/latex]

where [latex]a, b,[/latex] and [latex]c[/latex] are real numbers and [latex]a≠0[/latex].

When we talk about solving a quadratic, it means setting the function equal to zero, or [latex]y=0[/latex]. On a graph, this corresponds to the x-intercepts.

To solve quadratic functions, we primarily use the AC method (factoring), the square root method, and the quadratic formula.

Solve equations using the AC (Factoring) method

Zero Product Property

If the product of two terms A and B is equal to zero, then at least one of the factors must be equal to zero.

[latex]A\cdot B=0[/latex]

Implies

[latex]A=0\;or\;B=0[/latex]

Factoring: Type 1 if we can identify the greatest common factor directly.

Steps:

  1. Identify the greatest common factor (GCF) in all terms (numbers, variables, or both).
  2. Factor out the common part by writing it outside the parentheses.
  3. Write what’s left of each term inside the parentheses.
  4. Use the Zero Product Property to solve for [latex]x[/latex].

Example 2.1-2-1: Find zeros of the function.

[latex]f\left(x\right)=12x^2+4x[/latex]

Master L3 Key

Example 2.1-2-1: Find zeros of the function.

  1. Identify common factors: [latex]4x[/latex]

[latex]f\left(x\right)=12x^2+4x[/latex]

[latex]0=12x^2+4x[/latex]

  1. Factor out [latex]4x[/latex]
  2. Write what’s left [latex]\left(3x+1\right)[/latex]

[latex]0=4x\left(3x+1\right)[/latex]

  1. Use the Zero Product Property

[latex]4x=0[/latex]

[latex]x_1=0[/latex]

[latex]3x+1=0[/latex]

[latex]3x=-1[/latex]

[latex]x_2=-\frac13[/latex]

Answer: [latex]x=0[/latex] and [latex]x=-\frac13[/latex]

Polyno Character

Note:

[latex]x_{\color[rgb]{0.0, 0.44, 0.73}\mathbf1}\rightarrow The\;little\;{\color[rgb]{0.0, 0.44, 0.73}\mathbf1}\;means\;first\;x\;value[/latex]

[latex]x_{\color[rgb]{0.5, 0.0, 0.5}\mathbf2}\rightarrow The\;little\;{\color[rgb]{0.5, 0.0, 0.5}\mathbf2}\;means\;second\;x\;value[/latex]

These labels are often used in my math yard, especially when my yard has the same type of plants in one pot (like when a question has more than one answer). I use labels to mark the seeds (answers) to make sure I count all of them.

Your Turn

Practice 2.1-2-1

Practice 2.1-2-2

Factoring: Type 2, we can NOT directly identify the greatest common factor.

Steps:

  1. Check the equation — it should be in expanded (standard) form: [latex]f\left(x\right)=ax^2+bx+c[/latex]. (Sometimes you will see [latex]f\left(x\right)=ax^2+c[/latex])
  2. Identify the values of a, b, and c.
  3. Multiply a and c and use the AC method.
  4. Find two numbers such as:

#1⋅#2=ac, #1+ #2=b (you can use AC graph).

  1. Rewrite the function

If [latex]a=1[/latex] rewrite as [latex]\left(x+\#1\right)\left(x+\#2\right)[/latex]

If [latex]a≠1[/latex] rewrite as [latex]\left(x+\frac{\#1}a\right)\left(x+\frac{\#2}a\right)[/latex] divide each number by a.

  1. Set each factor equal to 0 and solve the resulting equations using the zero-product property:∙ [latex]B=0,\;then\;A=0\;or\;B=0[/latex]

Example 2.1-2-2: Find zeros of the function.

[latex]f\left(x\right)=x^2+2x-35[/latex]

Master L3 Key

Example 2.1-2-2: Find zeros of the function.

[latex]f\left(x\right)=x^2+2x-35[/latex]

  1. Check the equation — it should be in the expanded (standard) form: [latex]f\left(x\right)=ax^2+bx+c[/latex].

Yes, it is in the expanded (standard) form: [latex]f\left(x\right)=ax^2+bx+c[/latex].

  1. Identify the values of a, b, and c.

[latex]a=1, b=2, c=-35[/latex]

  1. Multiply a and c and use the AC method.

[latex]ac=-35[/latex]

  1. Find two numbers such as:

[latex]\#1\cdot\#2=ac,\;\#1+\#2=b[/latex]

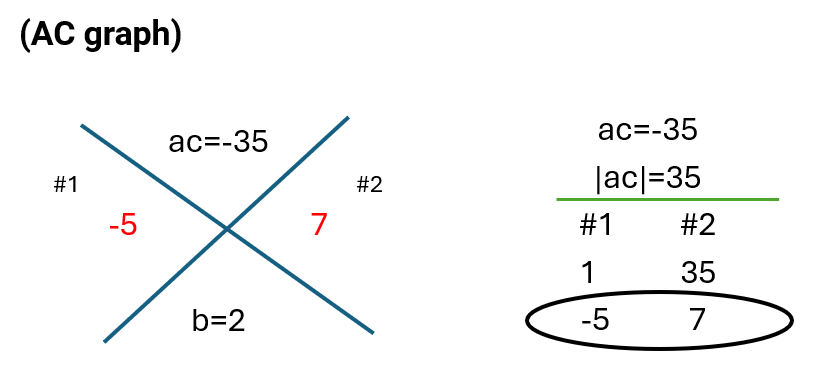
An image illustrating to find the zeros of a quadratic function, specifically f(x) = x squared + 2x - 35, by comparing it to the standard form f(x) = ax squared + bx + c. The image is divided into two main sections. On the left, a large 'X' diagram is shown. The top of the 'X' is labeled 'ac = -35', representing the product of the 'a' and 'c' coefficients (1 * -35 = -35). The bottom of the 'X' is labeled 'b = 2', representing the 'b' coefficient. The two diagonal arms of the 'X' are used to find two numbers that multiply to -35 and add up to 2. These numbers are found to be -5 and 7, which are written in red text on the left and right arms of the 'X' respectively, labeled '#1' and '#2'. On the right, a table-like structure further explains the process. The top part reiterates 'ac = -35' and shows '|ac| = 35'. Below this, a green line separates the 'ac' value from two columns labeled '#1' and '#2'. The first row below the line shows '1' and '35', which are factors of 35. The second-row shows '-5' and '7', which are the correct factors that satisfy both conditions (product is -35 and sum is 2). These numbers are encircled in black, highlighting them as the solution to the factoring problem.

You can find the correct number pair more easily by following these steps.

First, use the absolute value of ac and list all pairs of numbers whose product is [latex]∣ac∣[/latex].

Then, look at the original sign of [latex]ac[/latex]:

  • If [latex]ac[/latex] is negative, the pair must consist of one positive and one negative number.
  • If [latex]ac[/latex] is positive, both numbers in the pair must have the same sign.

To find the correct pair, also consider the value of [latex]b[/latex]. The sum of the two numbers must equal [latex]b[/latex].

In this question, since ac is negative, the pair must include one positive and one negative number. Their sum must be [latex]2[/latex].

So, the correct pair is −5 and 7.

  1. Rewrite the function

If [latex]a=1[/latex] rewrite as [latex]\left(x+\#1\right)\left(x+\#2\right)[/latex]

If [latex]a≠1[/latex] rewrite as [latex]\left(x+\frac{\#1}a\right)\left(x+\frac{\#2}a\right)[/latex]

Since [latex]a=1[/latex], then we can rewrite the function as

[latex]\left(x+\left(-5\right)\right)\left(x+\left(+7\right)\right)=0=>\left(x-5\right)\left(x+7\right)=0[/latex]

  1. Set each factor equal to 0 and solve the resulting equations using the zero-product property:∙ [latex]B=0,\;then\;A=0\;or\;B=0[/latex]

[latex]\left(x-5\right)\left(x+7\right)=0[/latex]

[latex]x-5=0[/latex]

[latex]x_1=5[/latex]

[latex]x+7=0[/latex]

[latex]x_2=-7[/latex]

Thus: [latex]x=5[/latex], and [latex]x=-7[/latex]

Example 2.1-2-3: Find zeros of the function.

[latex]f\left(x\right)=10x^2-19x+6[/latex]

Master L3 Key

Example 2.1-2-3: Find zeros of the function.

[latex]f\left(x\right)=10x^2-19x+6[/latex]

  1. Check the equation — it should be in the expanded (standard) form: [latex]f\left(x\right)=ax^2+bx+c[/latex].

Yes, it is in the expanded (standard) form: [latex]f\left(x\right)=ax^2+bx+c[/latex].

  1. Identify the values of a, b, and c.

[latex]a=10, b=-19, c=6[/latex]

  1. Multiply a and c and use the AC method.

[latex]ac=60[/latex]

  1. Find two numbers such as:

[latex]\#1\cdot\#2=ac,\;\#1+\#2=b[/latex]

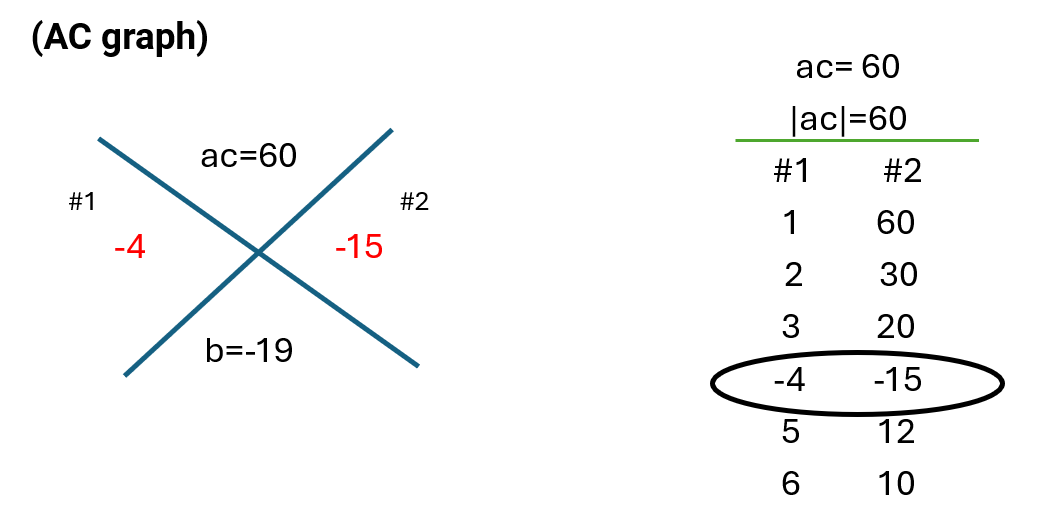
An image illustrating to find two numbers that multiply to 'ac' and add up to 'b' for a quadratic function. The image is divided into two main sections. On the left, a large 'X' diagram is shown. The top of the 'X' is labeled 'ac = 60', representing the product of the 'a' and 'c' coefficients. The bottom of the 'X' is labeled 'b = -19', representing the 'b' coefficient. The two diagonal arms of the 'X' are used to find two numbers that multiply to 60 and add up to -19. These numbers are found to be -4 and -15, which are written in red text on the left and right arms of the 'X' respectively, labeled '#1' and '#2'. On the right, a table-like structure further explains the process. The top part reiterates 'ac = 60' and shows '|ac| = 60'. Below this, a green line separates the 'ac' value from two columns labeled '#1' and '#2', listing pairs of factors of 60. The pairs shown are (1, 60), (2, 30), (3, 20), (-4, -15), (5, 12), and (6, 10). The pair '-4' and '-15' is encircled in black, highlighting them as the solution because their product is 60 and their sum is -19.

You can find the correct number pair more easily by following these steps.

First, use the absolute value of ac and list all pairs of numbers whose product is [latex]∣ac∣[/latex].

Then, look at the original sign of [latex]ac[/latex]:

  • If [latex]ac[/latex] is negative, the pair must consist of one positive and one negative number.
  • If [latex]ac[/latex] is positive, both numbers in the pair must have the same sign.

To find the correct pair, also consider the value of [latex]b[/latex]. The sum of the two numbers must equal [latex]b[/latex].

In this question, since ac is positive, the pair must be either both positive or both negative numbers. And their sum must be [latex]-19[/latex].

So, the correct pair is −4 and -15.

  1. Rewrite the function

If [latex]a=1[/latex] rewrite as [latex]\left(x+\#1\right)\left(x+\#2\right)[/latex]

If [latex]a≠1[/latex] rewrite as [latex]\left(x+\frac{\#1}a\right)\left(x+\frac{\#2}a\right)[/latex]

Since [latex]a≠1[/latex], then we can rewrite the function as

[latex]\left(x+\left(\frac{-4}{10}\right)\right)\left(x+\left(\frac{-15}{10}\right)\right)=0=>\left(x-\frac25\right)\left(x-\frac32\right)=0[/latex]

  1. Set each factor equal to 0 and solve the resulting equations using the zero-product property:∙ [latex]B=0,\;then\;A=0\;or\;B=0[/latex]

[latex]\left(x-\frac25\right)\left(x-\frac32\right)=0[/latex]

[latex]x-\frac25=0[/latex]

[latex]x_1=\frac25[/latex]

[latex]x-\frac32=0[/latex]

[latex]x_2=\frac32[/latex]

Thus: [latex]x=\frac25[/latex], and [latex]x=\frac32[/latex]

Your Turn

Practice 2.1-2-3

Practice 2.1-2-4

Practice 2.1-2-5

Solve equations using the Square Root method

Square Root Method

If the quadratic function does not have an [latex]x[/latex] term [latex]f\left(x\right)=ax^2+c[/latex], or if it is written as [latex]f\left(x\right)=a\left(x-h\right)^2+k[/latex], we can use the square root method to find the zeros.

If given a quadratic equation in the form [latex]f\left(x\right)=ax^2+\;c[/latex], and ask for finding real zeros/x-intercept/solve for [latex]x[/latex], we set the equation equal to zero, then solve.

[latex]ax^2+\;c=0[/latex]

[latex]ax^2=-c[/latex]

[latex]x^2=\frac{-c}a[/latex]

[latex]if\;\frac{-c}a\geq0[/latex]

[latex]if\;\frac{-c}a<0[/latex]

[latex]\sqrt{x^2}=\pm\sqrt{\frac{-c}a}[/latex]

Imaginary answer

[latex]x=\pm\sqrt{\frac{-c}a}[/latex]

(Not required in this course)

If given a quadratic equation in the form [latex]f\left(x\right)=a\left(x-h\right)^2+k[/latex], and asks to find the real zeros, x-intercepts, or solve for [latex]x[/latex], we set the equation equal to zero, follow the same steps as above, solve for [latex]x−h[/latex], and then find [latex]x[/latex].

[latex]a\left(x-h\right)^2+k=0[/latex]

[latex]a\left(x-h\right)^2=-k[/latex]

[latex]\left(x-h\right)^2=\frac{-k}a[/latex]

[latex]if\;\frac{-k}a\geq0[/latex]

[latex]if\;\frac{-k}a<0[/latex]

[latex]\sqrt{\left(x-h\right)^2}=\pm\sqrt{\frac{-c}a}[/latex]

Imaginary answer

[latex]\left(x-h\right)=\pm\sqrt{\frac{-c}a}[/latex]

[latex]x=\pm\sqrt{\frac{-c}a}-h[/latex]

(Not required in this course)

Example 2.1-3-1: Find zeros of the function.

[latex]f\left(x\right)=9x^2-25[/latex]

Master L3 Key

Example 2.1-3-1: Find zeros of the function.

[latex]f\left(x\right)=9x^2-25[/latex]

The given a quadratic equation in the form [latex]f\left(x\right)=ax^2+c[/latex], and ask for finding real zeros/x-intercept/solve for [latex]x[/latex], we set the equation equal to zero, then solve.

[latex]9x^2-25=0[/latex]

[latex]9x^2=25[/latex]

[latex]x^2=\frac{25}9\;Since\;\frac{25}9\geq0\;we\;continue\;the\;rest\;steps[/latex]

[latex]\sqrt{x^2}=\pm\sqrt{\frac{25}9}[/latex]

[latex]x=\pm\sqrt{\frac{25}9}[/latex]

[latex]x=\pm\frac53[/latex]

Thus [latex]x=\frac53[/latex] and [latex]x=-\frac53[/latex]

Example 2.1-3-2: Find zeros of the function.

[latex]f\left(x\right)=25x^2+6[/latex]

Master L3 Key

Example 2.1-3-2: Find zeros of the function.

[latex]f\left(x\right)=25x^2+6[/latex]

The given a quadratic equation in the form [latex]f\left(x\right)=ax^2+c[/latex], and ask for finding real zeros/x-intercept/solve for [latex]x[/latex], we set the equation equal to zero, then solve.

[latex]25x^2+6=0[/latex]

[latex]25x^2=-6[/latex]

[latex]x^2=\frac{-6}{25}[/latex]

Since [latex]\frac{-6}{25}<0[/latex] we ends here, since the answer is imaginary number, we say no real solution.

Thus [latex]x=\frac NA[/latex], no real solution.

Example 2.1-3-3: Find zeros of the function.

[latex]f\left(x\right)=3\left(x-2\right)^2-27[/latex]

Master L3 Key

Example 2.1-3-3: Find zeros of the function.

[latex]f\left(x\right)=3\left(x-2\right)^2-27[/latex]

The given a quadratic equation in the form [latex]f\left(x\right)=ax^2+c[/latex], and ask for finding real zeros/x-intercept/solve for [latex]x[/latex], we set the equation equal to zero, then solve.

[latex]3\left(x-2\right)^2-27=0[/latex]

[latex]3\left(x-2\right)^2=27[/latex]

[latex]\left(x-2\right)^2=9\;Since\;9\geq0\;we\;continue\;the\;rest\;steps[/latex]

[latex]\sqrt{\left(x-2\right)^2}=\pm\sqrt9\;[/latex]

[latex]x-2=\pm\sqrt9\;[/latex]

[latex]x-2=\pm3\;[/latex]

[latex]x-2=3[/latex]

[latex]x_1=5[/latex]

[latex]x-2=-3[/latex]

[latex]x_2=-1[/latex]

Thus [latex]x=5[/latex] and [latex]x=-1[/latex]

Polyno Character

When taking the square root of a variable, we must include both the positive and negative values, since raising a number to an even power eliminates its sign. For example, [latex]3^2=9[/latex] also [latex]\left(-3\right)^2=9[/latex]. If the base is unknown (unknown is under the even root), we must account for all possibilities, so we include both the positive and negative signs. However, if we have [latex]x=\sqrt9[/latex], we do not need to include the [latex]\pm[/latex] sign, because the variable is not under the square root.

Your Turn

Practice 2.1-3-1

Practice 2.1-3-2

Solve equations using the Quadratic Formula method

The given formula [latex]x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}[/latex]

is called the quadratic formula. It can solve any quadratic function (where the highest power of the unknown is 2).

Master L3 Character

This formula is often used when factoring, the AC method, or the square root method do not work. We usually keep it as an option because the calculations are more complex, and it’s easier to make mistakes, even though the method seems simple.

Steps to find zeros:

  1. Write in standard form [latex]ax^2+bx+c=0[/latex].
  2. Identify the variables [latex]a, b[/latex] and [latex]c[/latex].
  3. Substitute the variables [latex]a, b,[/latex] and [latex]c[/latex] into the quadratic formula:
  4. Simplify.
    • If [latex]b^2-4ac>0[/latex], then there will be 2 different real number solutions.
    • If [latex]b^2-4ac=0[/latex], then there will be 1 repeated real number solution.
    • If [latex]b^2-4ac<0[/latex], then there will be 2 non-real complex number solutions. (Answer contains i)
Master L3 Character

[latex]\ast b^2-4ac[/latex] is called the Discriminant and we use symbol [latex]\triangle[/latex] . We usually find the discriminant first to determine the type of solutions we will get (in step 4) and then decide whether or not to continue.

Example 2.1-4-1: Find zeros of the function.

[latex]f\left(x\right)=x^2+3x-8[/latex]

Master L3 Key

Example 2.1-4-1: Find zeros of the function.

[latex]f\left(x\right)=x^2+3x-8[/latex]

  1. Write in standard form [latex]ax^2+bx+c=0[/latex].

[latex]x^2+3x-8=0[/latex]

  1. Identify the variables [latex]a, b[/latex] and [latex]c[/latex].

[latex]a=1,\;b=3,\;c=-8[/latex]

  1. Substitute the variables [latex]a, b,[/latex] and [latex]c[/latex] into the quadratic formula:

[latex]x=\frac{-{\color[rgb]{0.5, 0.0, 0.5}\boldsymbol b}\pm\sqrt{{\color[rgb]{0.5, 0.0, 0.5}\boldsymbol b}^2-4{\color[rgb]{0.0, 0.44, 0.73}\boldsymbol a}{\color[rgb]{0.0, 0.0, 1.0}\boldsymbol c}}}{2{\color[rgb]{0.0, 0.44, 0.73}\boldsymbol a}}[/latex]

[latex]x=\frac{-\mathbf{\color[rgb]{0.5, 0.0, 0.5}\left(3\right)}\pm\sqrt{{\color[rgb]{0.5, 0.0, 0.5}\left(\mathbf3\right)}^2-4{\color[rgb]{0.0, 0.44, 0.73}\left(\mathbf1\right)}{\color[rgb]{0.0, 0.0, 1.0}\left(\boldsymbol-\mathbf8\right)}}}{2{\color[rgb]{0.0, 0.44, 0.73}\left(\mathbf1\right)}}[/latex]

  1. Simplify.

Find [latex]\triangle[/latex] first: [latex]b^2-4ac[/latex]

[latex]\left(3\right)^2-4\left(1\right)\left(-8\right)[/latex]

[latex]=9+32[/latex]

[latex]=41[/latex]

Since [latex]\triangle>0[/latex], thus we have two answers, continue the rest.

[latex]x=\frac{-3\pm\sqrt{41}}2[/latex]

Answer:

[latex]x=\frac{-3+\sqrt{41}}2,\;x=\frac{-3-\sqrt{41}}2[/latex]

Example 2.1-4-2: Find zeros of the function.

[latex]f\left(x\right)=2x^2-7x+35[/latex]

Master L3 Key

Example 2.1-4-2: Find zeros of the function.

[latex]f\left(x\right)=2x^2-7x+35[/latex]

  1. Write in standard form [latex]ax^2+bx+c=0[/latex].

[latex]2x^2-7x+35=0[/latex]

  1. Identify the variables [latex]a, b[/latex] and [latex]c[/latex].

[latex]a=2,\;b=-7,\;c=35[/latex]

  1. Substitute the variables [latex]a, b,[/latex] and [latex]c[/latex] into the quadratic formula:

[latex]x=\frac{-{\color[rgb]{0.5, 0.0, 0.5}\boldsymbol b}\pm\sqrt{{\color[rgb]{0.5, 0.0, 0.5}\boldsymbol b}^2-4{\color[rgb]{0.0, 0.44, 0.73}\boldsymbol a}{\color[rgb]{0.0, 0.0, 1.0}\boldsymbol c}}}{2{\color[rgb]{0.0, 0.44, 0.73}\boldsymbol a}}[/latex]

[latex]x=\frac{-\mathbf{\color[rgb]{0.5, 0.0, 0.5}\left({-7}\right)}\pm\sqrt{\mathbf{\color[rgb]{0.5, 0.0, 0.5}\left({-7}\right)}^2-4\mathbf{\color[rgb]{0.0, 0.44, 0.73}\left(2\right)}\mathbf{\color[rgb]{0.0, 0.0, 1.0}\left(35\right)}}}{2\mathbf{\color[rgb]{0.0, 0.44, 0.73}\left(2\right)}}[/latex]

  1. Simplify.

Find [latex]\triangle[/latex] first: [latex]b^2-4ac[/latex]

[latex]\left(-7\right)^2-4\left(2\right)\left(35\right)[/latex]

[latex]=49-280[/latex]

[latex]=-231[/latex]

Since [latex]\triangle<0[/latex], thus we imaginary answers, for this class we will say no real solution, and ends here.

Answer: No real solution.

Your Turn

Practice 2.1-4-1

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Math Mastery Manual Copyright © by Linglin (Niki) Liu is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book