"

2.5: Properties of Rational Functions

Learning Objectives

  1. Find the Domain of a Rational Function.
  2. Find the Vertical Asymptotes of a Rational Function.
  3. Find a Horizontal Asymptotes of a Rational Function.

Rational Function

A rational function is a function of the form.

[latex]R\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)}[/latex]

Where [latex]p[/latex] and [latex]q[/latex] are polynomial functions and [latex]q[/latex] is not the zero polynomial. The domain of [latex]R[/latex] is the set of all real numbers, except those for which the denominator [latex]q[/latex] is [latex]0[/latex].

Note: The domain of a rational function must be found before writing the function in its lowest terms.

Find the Domain of a Rational Function

Steps to Find the Domain

  1. Set the [latex]denominator ≠ 0[/latex]
    Because division by [latex]0[/latex] is not allowed.
  2. Solve for [latex]x[/latex]
    Find the values that make the denominator equal to [latex]0[/latex].
  3. Exclude those x-values from the domain
    These are the restrictions.
  4. Write the domain
    Use interval notation to show all allowed x-values.

Example 2.5-1-1: Find the domain of the rational function.

[latex]f\left(x\right)=\frac{x+2}{x^2+3x+2}[/latex]

Master L3 Key

Example 2.5-1-1: Find the domain of the rational function.

[latex]f\left(x\right)=\frac{x+2}{x^2+3x+2}[/latex]

  1. Set the [latex]denominator ≠ 0[/latex]

[latex]x^2+3x+2\neq0[/latex]

  1. Solve for [latex]x[/latex]
    Find the values that make the denominator equal to [latex]0[/latex].

[latex]x^2+3x+2=0[/latex]

[latex]\left(x+2\right)\left(x+1\right)=0[/latex]

[latex]x=-2,\;x=-1[/latex]

  1. Exclude those x-values from the domain
    These are the restrictions.

[latex]x\neq-2,\;x\neq-1[/latex]

  1. Write the domain
    Use interval notation to show all allowed x-values.

[latex] \left(-\infty,\;-2\right)\cup\left(-2,\;-1\right)\cup\left(-1,\;\infty\right)[/latex]

Your Turn

Practice 2.5-1-1

Find the Vertical Asymptotes of a Rational Function

The vertical asymptotes of a rational function may be found by examining the factors of the denominator that are not common to the factors in the numerator. Vertical asymptotes occur at the zeros of such factors.

How To

Given a rational function, identify any vertical asymptotes of its graph.

  1. Factor the numerator and denominator.
  2. Note any restrictions in the domain of the function.
  3. Reduce the expression by canceling common factors in the numerator and the denominator.
  4. Note any values that cause the denominator to be zero in this simplified version. These are where the vertical asymptotes occur.
  5. Note any restrictions in the domain where asymptotes do not occur. These are removable discontinuities, or “holes.”

Example 2.5-2-1: Find the vertical asymptotes of the function.

[latex]f\left(x\right)=\frac{5+2x^2}{2-x-x^2}[/latex]

Master L3 Key

Example 2.5-2-1: Find the vertical asymptotes of the function.

[latex]f\left(x\right)=\frac{5+2x^2}{2-x-x^2}[/latex]

First, factor the numerator and denominator.

[latex]k\left(x\right)=\frac{5+2x^2}{2-x-x^2}[/latex]

To find the vertical asymptotes, we determine where this function will be undefined by setting the denominator equal to zero:

[latex]\left(2+x\right)\left(1-x\right)=0[/latex]

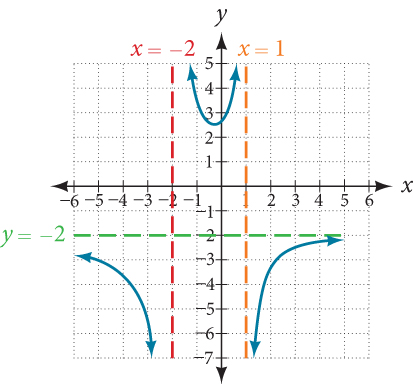
[latex]x=-2,\;1[/latex]

Neither [latex]x=–2[/latex] nor [latex]x=1[/latex] are zeros of the numerator, so the two values indicate two vertical asymptotes. The graph in Figure 9 confirms the location of the two vertical asymptotes.

A graph on a Cartesian coordinate system with the x-axis ranging from -6 to 6 and the y-axis ranging from -7 to 5, with grid lines at integer values. A blue curve is plotted, showing two distinct branches that approach vertical dashed lines. A vertical dashed red line is located at x = -2, and a vertical dashed orange line is located at x = 1. As the blue curve approaches these vertical lines from either side, the y-values tend towards positive or negative infinity, indicating that x = -2 and x = 1 are vertical asymptotes of the function represented by the blue curve. A dashed green horizontal line is also shown at y = -2, but the blue curve approaches this line as x goes to positive or negative infinity, suggesting that y = -2 is a horizontal asymptote.
Figure 9

Example 2.5-2-2: Find the vertical asymptotes of the function.

[latex]f\left(x\right)=\frac{x^2-1}{x^2-2x-3}[/latex]

Master L3 Key

Example 2.5-2-2: Find the vertical asymptotes of the function.

[latex]f\left(x\right)=\frac{x^2-1}{x^2-2x-3}[/latex]

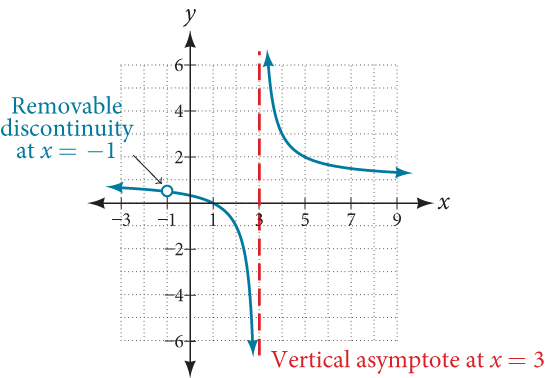
The function [latex]f\left(x\right)=\frac{x^2-1}{x^2-2x-3}[/latex] may be re-written by factoring the numerator and the denominator.

[latex]f\left(x\right)=\frac{\left(x+1\right)\left(x-1\right)}{\left(x+1\right)\left(x-3\right)}[/latex]

Notice that [latex]x+1[/latex] is a common factor to the numerator and the denominator. The zero of this factor, [latex]x=−1[/latex], is the location of the removable discontinuity. Notice also that [latex]x–3[/latex] is not a factor in both the numerator and denominator. The zero of this factor, [latex]x=3[/latex], is the vertical asymptote. See Figure 10. [Note that removable discontinuities may not be visible when we use a graphing calculator, depending upon the window selected.]

A graph of a rational function is shown on a Cartesian coordinate system. The x-axis ranges from -4 to 9, and the y-axis ranges from -6 to 6, with grid lines at integer values. A blue curve represents the function. There is a vertical dashed red line at x = 3, labeled 'Vertical asymptote at x = 3'. The blue curve approaches this line as x gets closer to 3 from both the left and the right, with the curve tending towards positive infinity on the right and negative infinity on the left. There is also a small open circle on the blue curve at x = -1, labeled 'Removable discontinuity at x = -1', indicating a hole in the graph at that point.
Figure 10

Your Turn

Practice 2.5-2-1

Horizontal Asymptotes of a Rational Function

Horizontal asymptotes help describe the behavior of a graph as the input gets very large or very small. Recall that a polynomial’s end behavior will mirror that of the leading term. Likewise, a rational function’s end behavior will mirror that of the ratio of the function that is the ratio of the leading terms.

There are three distinct outcomes when checking for horizontal asymptotes:

Case 1: If the [latex]degree\;of\;the\;denominator\;>\;degree\;of\;the\;numerator[/latex], there is a horizontal asymptote at [latex]y=0[/latex].

Example:

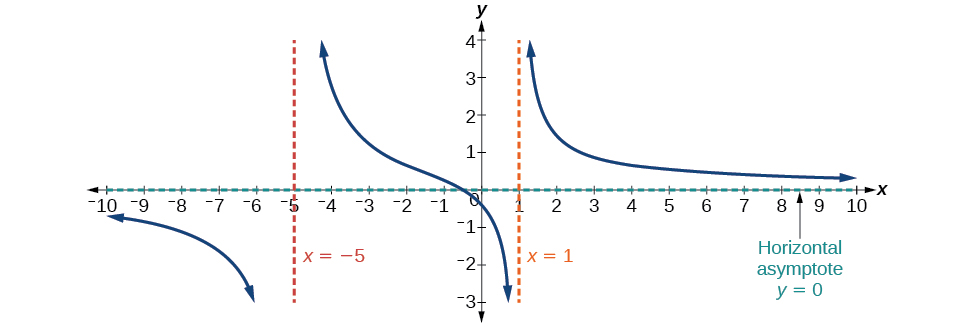
[latex]f\left(x\right)=\frac{4x+2}{x^2+4x-5}[/latex]

In this case, the end behavior is [latex]f\left(x\right)\approx\frac{4x}{x^2}=\frac4x[/latex]. This tells us that, as the inputs increase or decrease without bound, this function will behave similarly to the function [latex]g\left(x\right)=\frac4x[/latex], and the outputs will approach zero, resulting in a horizontal asymptote at [latex]y=0[/latex]. See Figure 12. Note that this graph crosses the horizontal asymptote.

A graph of a rational function is shown on a Cartesian coordinate system. The x-axis ranges from -10 to 10, and the y-axis ranges from -3 to 4, with grid lines at integer values. A dark blue curve represents the function, exhibiting two vertical asymptotes indicated by dashed lines: a red dashed line at x = -5 and an orange dashed line at x = 1. As the curve approaches these vertical lines, the y-values tend towards positive or negative infinity. A dashed teal horizontal line is located at y = 0, labeled 'Horizontal asymptote y = 0'. The blue curve approaches this horizontal line as x goes to positive or negative infinity.
Figure 12 Horizontal asymptote [latex]y=0[/latex]
when [latex]f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},\;q\left(x\right)\neq0[/latex] where [latex]degree\;of\;p>degree\;of\;q[/latex].

Case 2: If the [latex]degree\;of\;the\;denominator\;<\;degree\;of\;the\;numerator\;by\;one[/latex], we get a slant asymptote.

Example:

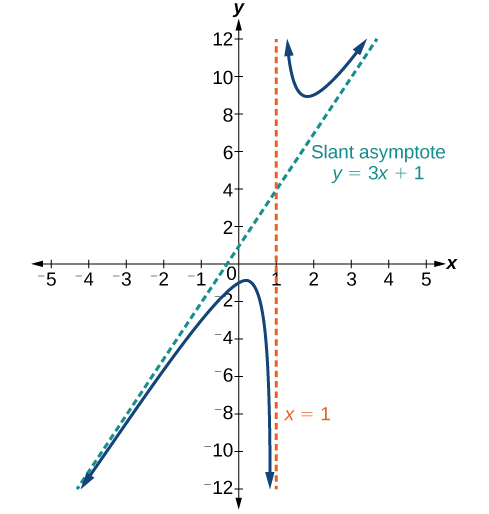
[latex]f\left(x\right)=\frac{3x^2-2x+1}{x-1}[/latex]

In this case, the end behavior is [latex]f\left(x\right)\approx\frac{3x^2}x=3x[/latex]. This tells us that as the inputs increase or decrease without bound, this function will behave similarly to the function [latex]g\left(x\right)=3x[/latex]. As the inputs grow large, the outputs will grow and not level off, so this graph has no horizontal asymptote. However, the graph of [latex]g\left(x\right)=3x[/latex] looks like a diagonal line, and since [latex]f[/latex] will behave similarly to [latex]g[/latex], it will approach a line close to [latex]y=3x[/latex]. This line is a slant asymptote.

To find the equation of the slant asymptote, divide [latex]\frac{3x^2-2x+1}{x-1}[/latex]. The quotient is [latex]3x+1[/latex], and the remainder is [latex]2[/latex]. The slant asymptote is the graph of the line [latex]g\left(x\right)=3x+1[/latex]. See Figure 13.

A graph of a rational function is shown on a Cartesian coordinate system. The x-axis ranges from -5 to 5, and the y-axis ranges from -12 to 12, with grid lines at integer values. A dark blue curve represents the function. There is a vertical dashed orange line at x = 1, labeled 'x = 1', which is a vertical asymptote. As the blue curve approaches this line, the y-values tend towards positive or negative infinity. A dashed teal line with the equation y = 3x + 1 is also plotted and labeled 'Slant asymptote y = 3x + 1'. As x approaches positive or negative infinity, the blue curve approaches this slant asymptote.
Figure 13 Slant asymptote when [latex]f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},\;q\left(x\right)\neq0[/latex], where [latex]degree\;of\;p>degree\;of\;q[/latex] by [latex]1[/latex].

Case 3: If the [latex]degree\;of\;the\;denominator\;=\;degree\;of\;the\;numerator[/latex], there is a horizontal asymptote at [latex]y=\frac{a_n}{b_n}[/latex], where [latex]a_n[/latex] and [latex]b_n[/latex] are the leading coefficients of [latex]p\left(x\right)[/latex] and [latex]q\left(x\right)[/latex] for  [latex]f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},\;q\left(x\right)\neq0[/latex].

Example:

[latex]f\left(x\right)=\frac{3x^2+2}{x^2+4x-5}[/latex]

In this case, the end behavior is [latex]f\left(x\right)\approx\frac{3x^2}{x^2}=3[/latex]. This tells us that as the inputs grow large, this function will behave like the function [latex]g\left(x\right)=3[/latex], which is a horizontal line. As [latex]x\rightarrow\pm\infty,\;f\left(x\right)\rightarrow3,[/latex] resulting in a horizontal asymptote at [latex]y=3[/latex]. See Figure 14. Note that this graph crosses the horizontal asymptote.

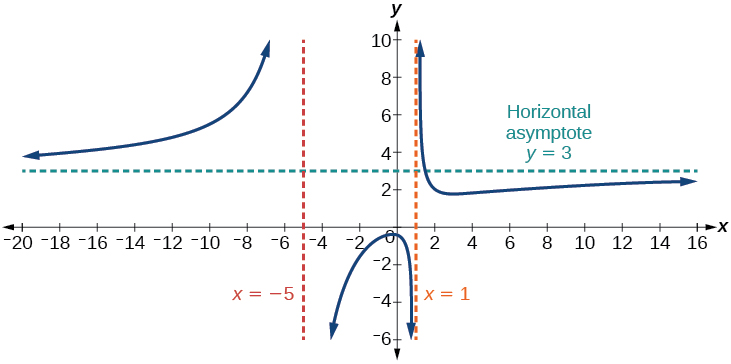
A graph of a rational function is shown on a Cartesian coordinate system. The x-axis ranges from -20 to 16, and the y-axis ranges from -6 to 10, with grid lines at intervals of 2 on the x-axis and 1 on the y-axis. A dark blue curve represents the function, exhibiting vertical asymptotes indicated by dashed lines: a red dashed line at x = -5 and an orange dashed line at x = 1. As the curve approaches these vertical lines, the y-values tend towards positive or negative infinity. A dashed teal horizontal line is located at y = 3, labeled 'Horizontal asymptote y = 3'. As x approaches positive or negative infinity (moving far to the left or right on the graph), the blue curve gets closer and closer to this horizontal line at y = 3 representing horizontal asymptote.
Figure 14 Horizontal asymptote when [latex]f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},\;q\left(x\right)\neq0[/latex], where [latex]degree\;of\;p>degree\;of\;q[/latex] by [latex]1[/latex].

Notice that, while the graph of a rational function will never cross a vertical asymptote, the graph may or may not cross a horizontal or slant asymptote. Also, although the graph of a rational function may have many vertical asymptotes, the graph will have at most one horizontal (or slant) asymptote.It should be noted that, if the degree of the numerator is larger than the degree of the denominator by more than one, the end behavior of the graph will mimic the behavior of the reduced end behavior fraction. For instance, if we had the function

[latex]f\left(x\right)=\frac{3x^5-x^2}{x+3}[/latex]

with end behavior

[latex]f\left(x\right)\approx\frac{3x^5}x=3x^4,[/latex]

the end behavior of the graph would look similar to that of an even polynomial with a positive leading coefficient.

[latex]x\rightarrow\pm\infty,\;f\left(x\right)\rightarrow\infty[/latex]

Steps for Finding Horizontal Asymptotes of a Rational Function

The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator.

  • Degree of numerator is less than degree of denominator: horizontal asymptote at [latex]y=0[/latex].
  • Degree of numerator is greater than degree of denominator by one: no horizontal asymptote; slant asymptote.
  • Degree of numerator is equal to degree of denominator: horizontal asymptote at ratio of leading coefficients.

Example 2.5-3-1: Find the horizontal asymptotes of the function.

[latex]f\left(x\right)=\frac{x^2-1}{5x^3-7x-6}[/latex]

Master L3 Key

Example 2.5-3-1: Find the horizontal asymptotes of the function.

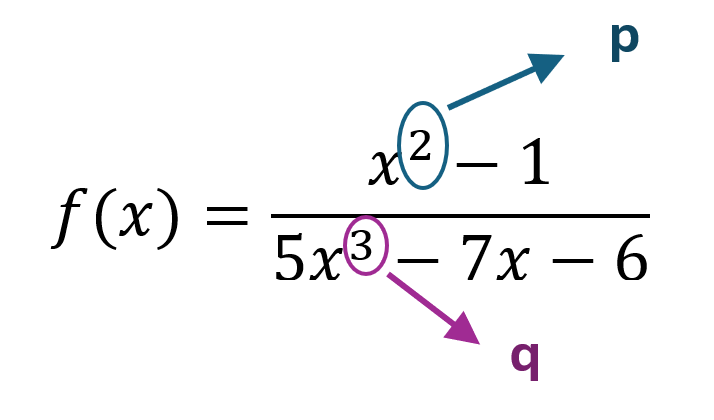
The function f(x) = (x square - 1) over (5x cube - 7x - 6) is shown. A teal arrow points to the highest power of x in the numerator, x square, labeled 'p'. A magenta arrow points to the highest power of x in the denominator, x cube, labeled 'q'.

Based on the rule: S

[latex]If\;p>p-1,\;and\;q>q-1,\;a\neq0\;and\;b\neq0[/latex]

[latex]f\left(x\right)=\frac{ax^p+cx^{p-1}\dots}{bx^q+dx^{q-1}\dots}[/latex]

If the numerator power [latex]p[/latex] is less than the denominator power [latex]q[/latex], the horizontal asymptote is [latex]y = 0[/latex] [latex]p < q[/latex], horizontal asymptote is [latex]y = 0[/latex].

If the numerator power [latex]p[/latex] is greater than the denominator power [latex]q[/latex], the horizontal asymptote is [latex]y = 0[/latex] [latex]p > q[/latex], horizontal asymptote does not exist.

If the numerator power [latex]p[/latex] is the same as the denominator power [latex]q[/latex], the horizontal asymptote is [latex]y=\frac ab[/latex] [latex]p = q[/latex], horizontal asymptote [latex]y=\frac ab[/latex].

Since [latex]p < q[/latex], horizontal asymptote is [latex]y = 0[/latex].

Your Turn

Practice 2.5-3-1

Practice 2.5-3-2

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Math Mastery Manual Copyright © by Linglin (Niki) Liu is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book