3.1: Composite Functions
Learning Objectives
- Create a new function by composition of functions.
- Evaluate composite functions.
- Find the domain of a composite function.
Composite Functions
If [latex]f[/latex] and [latex]g[/latex] are two functions, the composition of the function [latex]f[/latex] with the function [latex]g[/latex] is written as [latex]f\circ g[/latex].
[latex]\left(f\circ g\right)\left(x\right)=f\left(g\left(x\right)\right)[/latex]
We read the left-hand side as “[latex]f[/latex] composed with [latex]g[/latex] at [latex]x[/latex]”) and the right-hand side as “[latex]f[/latex] of [latex]g[/latex] of [latex]x[/latex].”
The two sides of the equation have the same mathematical meaning and are equal. The open circle symbol [latex]\circ[/latex] is called the composition operator.
| [latex]\mathbf{\color[rgb]{1.0, 1.0, 1.0}\left({f\circ g}\right)}\mathbf{\color[rgb]{1.0, 1.0, 1.0}\left(x\right)}{\color[rgb]{1.0, 1.0, 1.0}\mathbf=}{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol f}\mathbf{\color[rgb]{1.0, 1.0, 1.0}\left({g\left(x\right)}\right)}[/latex] | |
|---|---|
| [latex]\boldsymbol f\mathbf{\left({{\color[rgb]{0.0, 0.44, 0.73}g}{\color[rgb]{0.0, 0.44, 0.73}\left(x\right)}}\right)}[/latex] | [latex]g\left(x\right)[/latex], the output of [latex]g[/latex] is the input of [latex]f[/latex] |
| [latex]\boldsymbol f\mathbf{\left({g{\color[rgb]{0.0, 0.44, 0.73}\left(x\right)}}\right)}[/latex] | [latex]x[/latex] is the input of [latex]g[/latex] |
The domain of composite function must satisfy two things. Informally, any x-value must be
- In the domain of [latex]g[/latex] (the inside function).
- In the domain of [latex]f\circ g[/latex] (the simplified expression).
 |
Note:
[latex]\left(f\circ g\right)\left(x\right)\neq\left(f\cdot g\right)\left(x\right)[/latex] |
Example 3.1-1-1: Find its composite function.
Suppose [latex]f\left(x\right)=x^2[/latex] and [latex]g\left(x\right)=x+2[/latex]
[latex]\left(f\circ g\right)\left(x\right)[/latex]
 Key
Key
Example 3.1-1-1: Find its composite function. Suppose [latex]f\left(x\right)=x^2[/latex] and [latex]g\left(x\right)=x+2[/latex]
[latex]\left(f\circ g\right)\left(x\right)[/latex]
[latex]\left(f\circ g\right)\left(x\right)=f\left({\color[rgb]{0.86, 0.0, 0.0}\boldsymbol g}\mathbf{\color[rgb]{0.86, 0.0, 0.0}\left(x\right)}\right)[/latex]
[latex]=f\left({\color[rgb]{0.86, 0.0, 0.0}\boldsymbol x}{\color[rgb]{0.86, 0.0, 0.0}\mathbf+}{\color[rgb]{0.86, 0.0, 0.0}\mathbf2}\right)\; Use\;x+2\;replaces\;g\left(x\right)[/latex]
[latex]={\color[rgb]{0.0, 0.44, 0.73}\boldsymbol f}\mathbf{\color[rgb]{0.0, 0.44, 0.73}\left({x+2}\right)}[/latex]
[latex]=\mathbf{\left({{\color[rgb]{0.0, 0.44, 0.73}x}{\color[rgb]{0.0, 0.44, 0.73}+}{\color[rgb]{0.0, 0.44, 0.73}2}}\right)}^2\boldsymbol\; Use\;x+2\;replaces\;x\;in\;function\;f[/latex]
[latex]=x^2+4x+4\boldsymbol\; Foil\;and\;simplify[/latex]
[latex]\left(f\circ g\right)\left(x\right)=x^2+4x+4[/latex]
Example 3.1-1-2: Find its composite function.
Suppose [latex]f\left(x\right)=x^2[/latex] and [latex]g\left(x\right)=x+2[/latex]
[latex]\left(g\circ f\right)\left(x\right)[/latex]
 Key
Key
Example 3.1-1-2: Find its composite function. Suppose [latex]f\left(x\right)=x^2[/latex] and [latex]g\left(x\right)=x+2[/latex]
[latex]\left(g\circ f\right)\left(x\right)[/latex]
[latex]\left(g\circ f\right)\left(x\right)=g\left({\color[rgb]{0.86, 0.0, 0.0}\boldsymbol f}\mathbf{\color[rgb]{0.86, 0.0, 0.0}\left(x\right)}\right)[/latex]
[latex]=g\left({\color[rgb]{0.86, 0.0, 0.0}\boldsymbol x}^{\color[rgb]{0.86, 0.0, 0.0}\mathbf2}\right) Use\;x^2\;replaces\;f\left(x\right)[/latex]
[latex]={\color[rgb]{0.0, 0.44, 0.73}\boldsymbol g}\mathbf{\color[rgb]{0.0, 0.44, 0.73}\left(x^2\right)}[/latex]
[latex]=\mathbf{\left({\color[rgb]{0.0, 0.44, 0.73}x}^{\color[rgb]{0.0, 0.44, 0.73}2}\right)}+2 Use\;x^2\;replaces\;x\;in\;function\;g[/latex]
[latex]=x^2+2 Simplify[/latex]
[latex]\left(g\circ f\right)\left(x\right)=x^2+2[/latex]
 Your Turn
Your Turn
Practice 3.1-1-1
Evaluate composite functions
Given a formula for a composite function, evaluate the function.
- Evaluate the inside function using the input value or variable provided.
- Use the resulting output as the input to the outside function.
Example 3.1-2-1: Find its composite function.
Suppose [latex]f\left(x\right)=x^2[/latex] and [latex]g\left(x\right)=x+2[/latex]
[latex]\left(f\circ g\right)\left(1\right)[/latex]
 Key
Key
Example 3.1-2-1: Find its composite function. Suppose [latex]f\left(x\right)=x^2[/latex] and [latex]g\left(x\right)=x+2[/latex]
[latex]\left(f\circ g\right)\left(1\right)[/latex]
[latex]\left(f\circ g\right)\left(1\right)=f\left({\color[rgb]{0.86, 0.0, 0.0}\boldsymbol g}\mathbf{\color[rgb]{0.86, 0.0, 0.0}\left(1\right)}\right) Use\;x+2\;replaces\;g\left(x\right)\;and\;x=1,\;thus\;find\;g\left(1\right)[/latex]
[latex]{\color[rgb]{0.86, 0.0, 0.0}\boldsymbol g}\mathbf{\color[rgb]{0.86, 0.0, 0.0}\left(1\right)}{\color[rgb]{0.86, 0.0, 0.0}\mathbf=}{\color[rgb]{0.86, 0.0, 0.0}\mathbf1}{\color[rgb]{0.86, 0.0, 0.0}\mathbf+}{\color[rgb]{0.86, 0.0, 0.0}\mathbf2}{\color[rgb]{0.86, 0.0, 0.0}\mathbf=}{\color[rgb]{0.0, 0.44, 0.73}\mathbf3}[/latex]
[latex]=f\left({\color[rgb]{0.0, 0.44, 0.73}\mathbf3}\right) Use\;{\color[rgb]{0.0, 0.44, 0.73}\mathbf3}\;replaces\;{\color[rgb]{0.86, 0.0, 0.0}\boldsymbol g}\mathbf{\color[rgb]{0.86, 0.0, 0.0}\left(1\right)}\;in\;function\;f[/latex]
[latex]=\left(3\right)^2 Solve[/latex]
[latex]=9[/latex]
[latex]\left(f\circ g\right)\left(1\right)=9[/latex]
 Your Turn
Your Turn
Practice 3.1-2-1
Find the domain of a composite function
Domain of a Composite Function
The domain of a composite function [latex]f\left(g\left(x\right)\right)[/latex] is the set of those inputs [latex]x[/latex] in the domain of [latex]g[/latex] for which [latex]g\left(x\right)[/latex] is in the domain of [latex]f[/latex].
Given a function composition [latex]f\left(g\left(x\right)\right)[/latex], determine its domain.
- Find the domain of [latex]g[/latex].
- Find the domain of [latex]f[/latex].
- Find those inputs [latex]x[/latex] in the domain of [latex]g[/latex] for which [latex]g\left(x\right)[/latex] is in the domain of [latex]f[/latex]. That is, exclude those inputs [latex]x[/latex] from the domain of [latex]g[/latex] for which [latex]g\left(x\right)[/latex] is not in the domain of [latex]f[/latex]. The resulting set is the domain of [latex]f\circ g[/latex].
Example 3.1-3-1: Finding the domain of the composite function.
[latex]\left(f\circ g\right)\left(x\right)[/latex] where [latex]f\left(x\right)=\sqrt x+2[/latex] and [latex]g\left(x\right)=\sqrt3-x[/latex]
 Key
Key
Example 3.1-3-1:Finding the domain of the composite function.
[latex]\left(f\circ g\right)\left(x\right)[/latex] where [latex]f\left(x\right)=\sqrt x+2[/latex] and [latex]g\left(x\right)=\sqrt3-x[/latex]
Rewrite format: [latex]\left(f\circ g\right)\left(x\right)=f\left(g\left(x\right)\right)[/latex]
Step 1: find the domain of [latex]g\left(x\right)[/latex].
[latex]g\left(x\right)=3-x,\;x[/latex] can be any number, since it is not under an even root or in the denominator.
Step 2: Find [latex]f\left(g\left(x\right)\right)[/latex].
[latex]f\left(g\left(x\right)\right)=\sqrt{3-x}+2[/latex]
Step 3: Find the domain of [latex]f\left(g\left(x\right)\right)[/latex].
Since [latex]f\left(g\left(x\right)\right)=\sqrt{3-x}+2,\;x[/latex] is under even root, thus restriction applies.
If [latex]\left(A\right)=\sqrt A[/latex], then [latex]A\geq0[/latex]
[latex]3-x\geq0[/latex]
[latex]3\geq x[/latex]
[latex]x\leq3[/latex]
Overall [latex]x\geq0[/latex], and [latex]x\leq3[/latex], thus the real domain of [latex]f\left(g\left(x\right)\right)[/latex] is
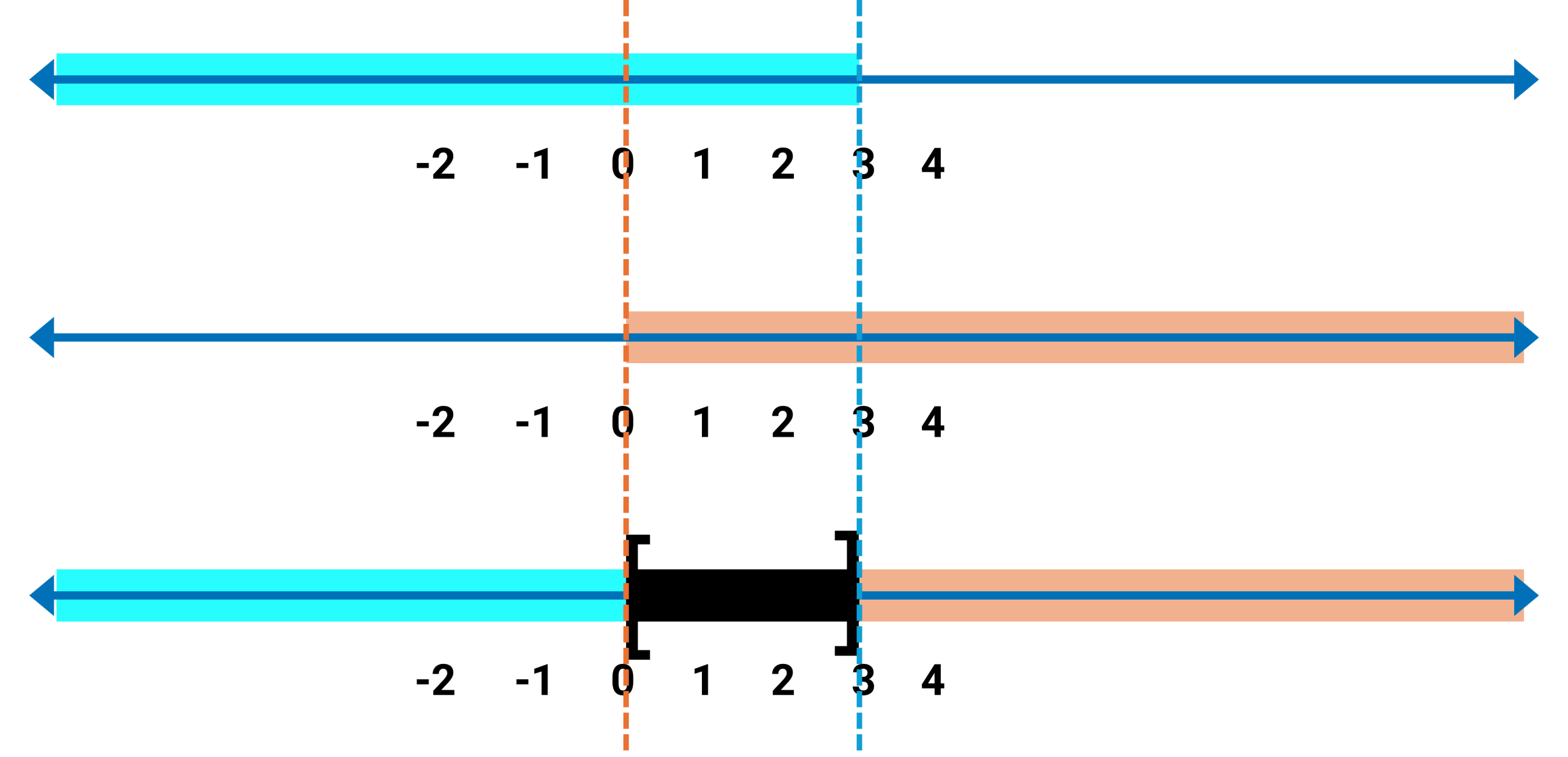
[latex][0, 3][/latex]
Note that the domain depends on both the function [latex]f\left(g\left(x\right)\right)[/latex]and the inner function [latex]g\left(x\right)[/latex]. Specifically, we must first ensure that [latex]x[/latex] is in the domain of [latex]g\left(x\right)[/latex] and then that [latex]g\left(x\right)[/latex] lies within the domain of [latex]f[/latex]. In other words, the domain of [latex]f\left(g\left(x\right)\right)[/latex] consists of all values of [latex]x[/latex] such that:
- [latex]x[/latex] is in the domain of [latex]g[/latex], and
- [latex]g\left(x\right)[/latex] is in the domain of [latex]f[/latex].
Licenses and Attribution
CC Licensed Content
- College-algebra-2e by Jay Abramson is licensed CC BY. Access for free.

