"

3.2: One-to-One Functions; Inverse Functions

Learning Objectives

  1. Determine when a function is one-to-one.
  2. Find the inverse of a function.
  3. Determine if a pair of functions are inverses.

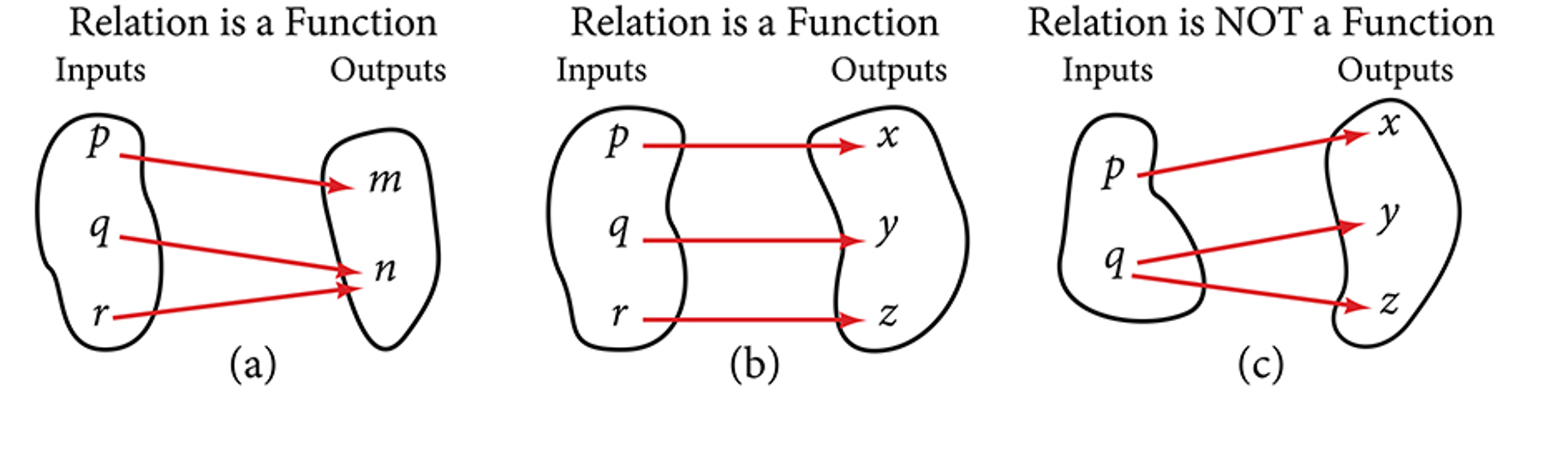
One-to-one Function

A function is one-to-one if any two different inputs in the domain correspond to two different outputs in the range. That is, if [latex]x_1[/latex]and [latex]x_2[/latex] are two different inputs of a function [latex]f[/latex], then [latex]f[/latex] is one-to-one if [latex]f\left(x_1\right)\neq f\left(x_2\right)[/latex]

Three diagrams illustrate the concept of a function using mappings between inputs and outputs. Each diagram shows two irregularly shaped bubbles labeled 'Inputs' and 'Outputs', with red arrows indicating the mapping from input to output. Diagram (a), titled 'Relation is a Function', shows inputs p, q, and r. Input p maps to output m, input q maps to output n, and input r maps to output n. This represents a function because each input has exactly one output. Diagram (b), also titled 'Relation is a Function', shows inputs p, q, and r. Input p maps to output x, input q maps to output y, and input r maps to output z. This also represents a function as each input has a unique output. Diagram (c), titled 'Relation is NOT a Function', shows inputs p and q. Input p maps x while input q maps to two different outputs, y and z. This is not a function because the input q has more than one output.

In a graph, a one-to-one function must pass both the vertical line test and the horizontal line test.”

Explanation:

  • Vertical Line Test: This test determines if a graph represents a function.
  • Horizontal Line Test: This test checks if a function is one-to-one.

Note: it must pass both tests.

Example 3.2-1-1: Identify if the graph is one to one function.

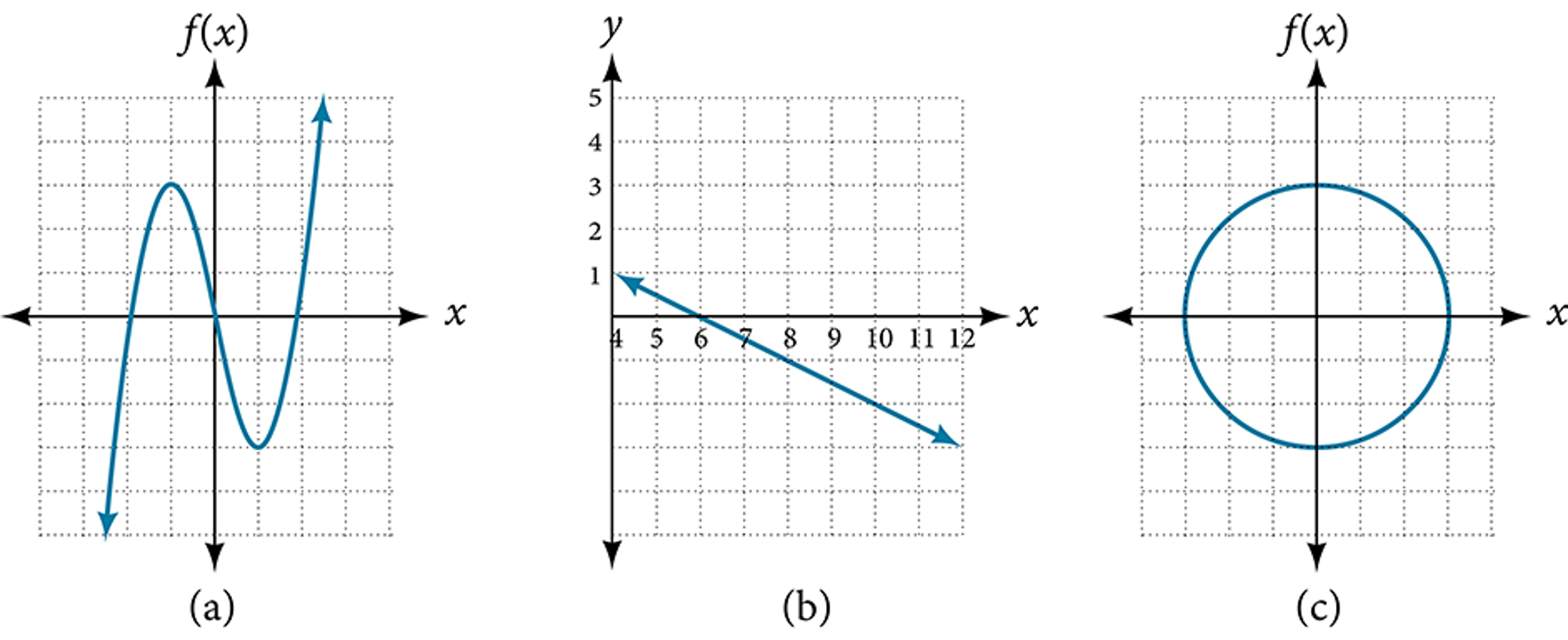
Three graphs labeled (a), (b), and (c) are shown on Cartesian coordinate systems to determine if they represent one-to-one functions. Graph (a) shows a cubic-like function. Graph (b) shows a linear function with a negative slope. Graph (c) shows a circle centered at the origin.

Inverselina Character Key

Example 3.2-1-1: Identify if the graph is one to one function. 

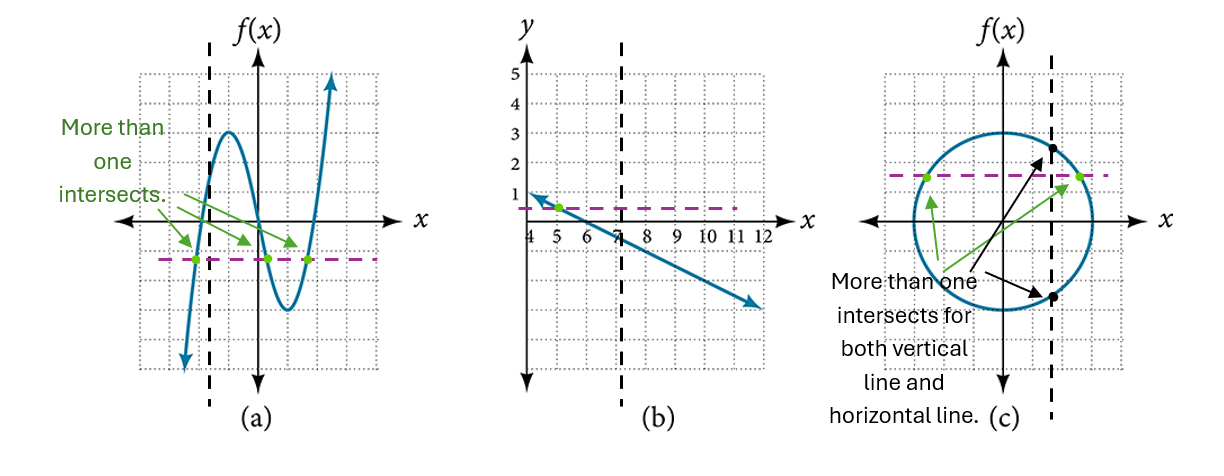
Three graphs labeled (a), (b), and (c) are shown on Cartesian coordinate systems to illustrate the vertical line test for determining if a graph represents a function. Graph (a) shows a teal curve. A dashed purple vertical line is drawn, intersecting the curve at three distinct green points. Green arrows point from the vertical line to each of these intersection points, and the text 'More than one intersects' is written in green Graph (b) shows a teal straight line with a negative slope. A dashed purple vertical line is drawn, a green point is shown on the line. Graph (c) shows a teal circle centered at the origin. A dashed purple vertical line is drawn, intersecting the circle at two distinct green points. Green arrows point from the vertical line to each of these intersection points. Additionally, a dashed purple horizontal line is drawn 2, also intersecting the circle at two black points. The text 'More than one intersects for both vertical line and horizontal line' is written in black.

  1. Function passes vertical line test, NOT one-to-one function, DID NOT passes horizontal line test.
  2. Function passes vertical line test, one-to-one function, passes horizontal line test.
  3. Not a function

Three diagrams illustrate the concept of a function using mappings between inputs and outputs. Each diagram shows two irregularly shaped bubbles labeled 'Inputs' and 'Outputs', with red arrows indicating the mapping from input to output. Diagram (a), titled 'Relation is a Function', shows inputs p, q, and r. Input p maps to output m, input q maps to output n, and input r maps to output n. This represents a function because each input has exactly one output. Diagram (b), also titled 'Relation is a Function', shows inputs p, q, and r. Input p maps to output x, input q maps to output y, and input r maps to output z. This also represents a function as each input has a unique output. Diagram (c), titled 'Relation is NOT a Function', shows inputs p and q. Input p maps x while input q maps to two different outputs, y and z. This is not a function because the input q has more than one output. Your Turn

Practice 3.2-1-1

Inverse of a function

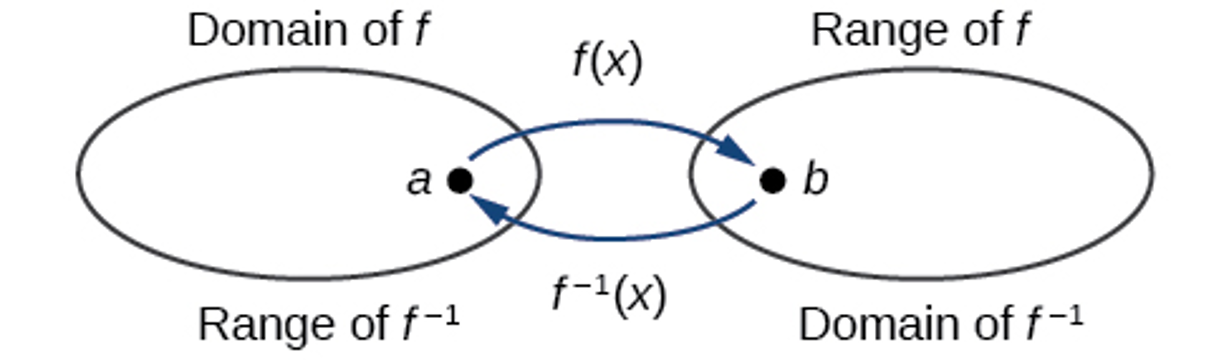
For any one-to-one function [latex]f\left(x\right)=y[/latex], a function [latex]f^{-1}\left(x\right)[/latex] is an inverse function of [latex]f[/latex] if [latex]f^{-1}\left(y\right)=x[/latex]. This can also be written as [latex]f^{-1}\left(f\left(x\right)\right)=x[/latex] for all [latex]x[/latex] in the domain of [latex]f[/latex]. It also follows that [latex]f\left(f^{-1}\left(x\right)\right)=x[/latex] for all [latex]x[/latex] in the domain of [latex]f^{-1}[/latex] if [latex]f^{-1}[/latex] is the inverse of [latex]f[/latex].

The notation [latex]f^{-1}[/latex] is read “[latex]f[/latex] inverse.” Like any other function, we can use any variable name as the input for [latex]f^{-1}[/latex], so we will often write [latex]f^{-1}\left(x\right)[/latex], which we read as “[latex]f[/latex] inverse of [latex]x[/latex]“. Keep in mind that

[latex]f^{-1}\left(x\right)\neq\frac1{f\left(x\right)}[/latex]

and not all functions have inverses.

If [latex]f[/latex] has its inverse function [latex]f^{-1}[/latex], then the domain of [latex]f[/latex] is the range of [latex]f^{-1}[/latex], the range of [latex]f[/latex] is the domain of [latex]f^{-1}[/latex].

A diagram illustrating the relationship between a function f(x) and its inverse function f inverse x using ovals to represent sets. An oval on the left is labeled 'Domain of f' and 'Range of f inverse'. It contains a single element labeled 'a'. An oval on the right is labeled 'Range of f' and 'Domain of f inverse'. It contains a single element labeled 'b'. A blue arrow labeled 'f(x)' points from 'a' in the left oval to 'b' in the right oval, indicating that the function f maps 'a' to 'b'. A blue arrow labeled 'f inverse (x)' points from 'b' in the right oval back to 'a' in the left oval, indicating that the inverse function f inverse maps 'b' back to 'a'.

To find inverse function:

Step 1: Substitute the function name for [latex]y[/latex], if needed.

Step 2: Replace [latex]x[/latex] with [latex]y[/latex], and [latex]y[/latex] with [latex]x[/latex].

Step 3: Isolate [latex]y[/latex].

Step 4: use [latex]f^{-1}[/latex] substitute the [latex]y[/latex].

Example 3.2-2-1: Identify the domain and range of the given function. Then, find its inverse function and determine the domain and range of the inverse.

[latex]f\left(x\right)=\frac2{x+3}[/latex]

Inverselina Character Key

Example 3.2-2-1: Identify the domain and range of the given function. Then, find its inverse function and determine the domain and range of the inverse.

[latex]f\left(x\right)=\frac2{x+3}[/latex]

Domain of [latex]f\left(x\right)=\frac2{x+3}[/latex]

[latex]x+3\neq0[/latex]

[latex]x\neq-3[/latex]

Range of [latex]f\left(x\right)=\frac2{x+3}[/latex]

Since [latex]x\neq-3[/latex] thus [latex]y\neq0[/latex]

Inverse function of [latex]f\left(x\right)=\frac2{x+3}[/latex]

Two steps for substituting and replacing variables in a function. Step 1: Substitute the function name for y, if needed. To the right of the text, the equation f of x equals 2 over x plus 3 is shown. A purple 'y' is written above the 'f of x' and an 'X' is drawn through the 'f of x'. Below this, the equation y equals 2 over x plus 3 is shown. Step 2: Replace x with y, and y with x. To the right of the text, the equation y equals 2 over x plus 3 is displayed. A blue arrow points down from the 'y' on the left side of the equation, and another blue arrow points down from the 'x' in the denominator on the right side of the equation. Below this, the equation x equals 2 over y plus 3 is shown, with a purple 'x' replacing the 'y' and a green 'y' replacing the 'x'.

Step 3: Isolate [latex]y[/latex].

[latex]x=\frac2{y+3}[/latex]

[latex]\left(y+3\right)x=\frac2{y+3}\left(y+3\right)[/latex]

[latex]xy+3x=2[/latex]

[latex]xy=2-3x[/latex]

[latex]y=\frac{2-3x}x[/latex]

Step 4: use [latex]f^{-1}[/latex] substitute the [latex]y[/latex].

[latex]f^{-1}\left(x\right)=\frac{2-3x}x   \left(Replace\;y\;by\;f^{-1}\left(x\right)\right)[/latex]

Domain of the inverse function

[latex]f^{-1}\left(x\right)\;is\;x\neq0[/latex] (range of the original function)

Range of the inverse function

[latex]f^{-1}\left(x\right)\;is\;y\neq-3[/latex] (domain of the original function)

Three diagrams illustrate the concept of a function using mappings between inputs and outputs. Each diagram shows two irregularly shaped bubbles labeled 'Inputs' and 'Outputs', with red arrows indicating the mapping from input to output. Diagram (a), titled 'Relation is a Function', shows inputs p, q, and r. Input p maps to output m, input q maps to output n, and input r maps to output n. This represents a function because each input has exactly one output. Diagram (b), also titled 'Relation is a Function', shows inputs p, q, and r. Input p maps to output x, input q maps to output y, and input r maps to output z. This also represents a function as each input has a unique output. Diagram (c), titled 'Relation is NOT a Function', shows inputs p and q. Input p maps x while input q maps to two different outputs, y and z. This is not a function because the input q has more than one output. Your Turn

Practice 3.2-2-1

Determine if a pair of functions are inverses

Given two functions [latex]f\left(x\right)[/latex] and [latex]g\left(x\right)[/latex], test whether the functions are inverses of each other.

  1. Determine whether [latex]f\left(g\left(x\right)\right)=x[/latex] or [latex]g\left(f\left(x\right)\right)=x[/latex].
  2. If either statement is true, then both are true, and [latex]g=f^{-1}[/latex] and [latex]f=g^{-1}[/latex]. If either statement is false, then both are false, and [latex]g\neq f^{-1}[/latex] and [latex]f\neq g^{-1}[/latex].

Example 3.2-3-1: Testing Inverse Relationships Algebraically

If [latex]f\left(x\right)=\frac1{x+2}[/latex] and [latex]g\left(x\right)=\frac1x-2[/latex], is [latex]g=f^{-1}[/latex]?

Inverselina Character Key

Example 3.2-3-1: Testing Inverse Relationships Algebraically

If [latex]f\left(x\right)=\frac1{x+2}[/latex] and [latex]g\left(x\right)=\frac1x-2[/latex], is [latex]g=f^{-1}[/latex]?

[latex]g\left(f\left(x\right)\right)=\frac1{\left({\displaystyle\frac1{x+2}}\right)}-2[/latex]

[latex]=x+2-2[/latex]

[latex]=x[/latex]

We must also verify the other formula.

[latex]f\left(g\left(x\right)\right)=\frac1{{\displaystyle\frac1x}-2+2}[/latex]

[latex]=\frac1{\displaystyle\frac1x}[/latex]

[latex]=x[/latex]

so

[latex]g=f^{-1}[/latex] and [latex]f=g^{-1}[/latex]

Inverselina CharacterAnalysis

Notice the inverse operations are in reverse order of the operations from the original function.

Three diagrams illustrate the concept of a function using mappings between inputs and outputs. Each diagram shows two irregularly shaped bubbles labeled 'Inputs' and 'Outputs', with red arrows indicating the mapping from input to output. Diagram (a), titled 'Relation is a Function', shows inputs p, q, and r. Input p maps to output m, input q maps to output n, and input r maps to output n. This represents a function because each input has exactly one output. Diagram (b), also titled 'Relation is a Function', shows inputs p, q, and r. Input p maps to output x, input q maps to output y, and input r maps to output z. This also represents a function as each input has a unique output. Diagram (c), titled 'Relation is NOT a Function', shows inputs p and q. Input p maps x while input q maps to two different outputs, y and z. This is not a function because the input q has more than one output. Your Turn

Practice 3.2-3-1

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Math Mastery Manual Copyright © by Linglin (Niki) Liu is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book