"

3.3: Exponential Functions

Learning Objectives

  1. Evaluate exponential functions.
  2. List the properties of exponential functions and their graphs.
  3. Solve exponential equations.

Evaluating Exponential Functions

For any real number [latex]x[/latex], an exponential function is a function with the form

[latex]f\left(x\right)=ab^x[/latex]

where

  • [latex]a[/latex] is a non-zero real number called the initial value and
  • [latex]b[/latex] is any positive real number such that [latex]b\neq1[/latex].
  • The domain of [latex]f[/latex] is all real numbers.
  • The range of [latex]f[/latex] is all positive real numbers if [latex]a>0[/latex].
  • The range of [latex]f[/latex] is all negative real numbers if [latex]a<0[/latex].
  • The y-intercept is [latex]\left(0,\;a\right)[/latex], and the horizontal asymptote is [latex]y=0[/latex].
Inversilina Character

It is important to correctly identify the base of an exponential function. In the standard form [latex]f\left(x\right)=ab^x[/latex], the variable [latex]x[/latex] is the exponent, [latex]b[/latex] represents the base, and [latex]a[/latex] is a constant coefficient. Please refer to the attached image for clarification.

[latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol f}\mathbf{\color[rgb]{1.0, 1.0, 1.0}\left(x\right)}{\color[rgb]{1.0, 1.0, 1.0}\mathbf=}{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol a}{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol b}^{\color[rgb]{1.0, 1.0, 1.0}\mathbf x}[/latex]
[latex]a[/latex] Coefficient
[latex]b[/latex] Base
[latex]x[/latex] Power/exponent

Example 3.3-1-1: Identifying Exponential Functions: Identify the base of the exponential function. And find the value for part c and d

  1. [latex]f\left(x\right)=4^{3\left(x-2\right)}[/latex]
  2. [latex]f\left(x\right)=0.35e^{3+x}[/latex]
  3. [latex]f\left(x\right)=-\frac13^2[/latex]
  4. [latex]f\left(x\right)=\left(-\frac13\right)^2[/latex]

Inverselina Character Key

Example 3.3-1-1: Identifying Exponential Functions: Identify the base of the exponential function. And find the value for part c and d

  1. [latex]f\left(x\right)=4^{3\left(x-2\right)}[/latex]
  2. [latex]f\left(x\right)=0.35e^{3+x}[/latex]
  3. [latex]f\left(x\right)=-\frac13^2[/latex]
  4. [latex]f\left(x\right)=\left(-\frac13\right)^2[/latex]
  1. [latex]f\left(x\right)=4^{3\left(x-2\right)}[/latex] the base is [latex]4[/latex].
  2. [latex]f\left(x\right)=0.35e^{3+x}[/latex] the base is [latex]e[/latex].
  3. [latex]f\left(x\right)=-\frac13^2[/latex] the base is [latex]\frac13[/latex].

[latex]f\left(x\right)=-\cdot\frac13\cdot\frac13=-\frac19[/latex]

  1. [latex]f\left(x\right)=\left(-\frac13\right)^2[/latex] the base is [latex]-\frac13[/latex].

[latex]f\left(x\right)=\left(-\frac13\right)\left(-\frac13\right)=\frac19[/latex]

Your Turn

Practice 3.3-1-1

Properties of Exponential Functions

[latex]f\left(x\right)=a^x\;or\;y=a^x,\;where\;a>0,\;a\neq1,\;and\;x\in\mathbb{R}\;\left(Domain\right),\;f\left(x\right)>0\left(range\right).[/latex] The shape of the graph of [latex]f\left(x\right)=a^x[/latex] is given by:

  • If [latex]0<[/latex] [latex]a<1[/latex], then the function decreases from left to right.

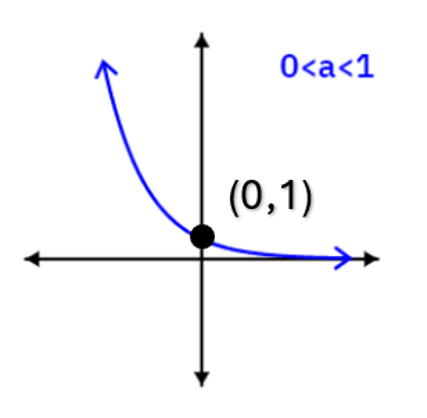
A graph of a decreasing exponential function on a Cartesian coordinate system. The x and y axes intersect at the origin. A blue curve starts high in the second quadrant, passes through the point (0, 1), which is marked with a black dot and labeled, and then decreases asymptotically towards the positive x-axis in the first quadrant. The label '0 < a < 1' in blue indicates that the base 'a' of the exponential function is between 0 and 1, which accounts for the decreasing nature of the graph.

  • If [latex]a>1[/latex], then the function increases from left to right.

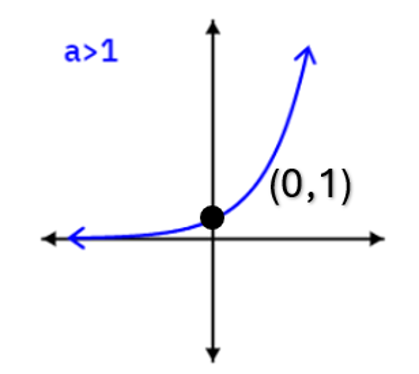
A graph of an increasing exponential function on a Cartesian coordinate system. The x and y axes intersect at the origin. A blue curve starts close to the negative x-axis in the third quadrant, passes through the point (0, 1), which is marked with a black dot and labeled, and then increases rapidly into the first quadrant. The label 'a > 1' in blue indicates that the base 'a' of the exponential function is greater than 1, which accounts for the increasing nature of the graph.

  • Both always pass [latex](0,1)[/latex].
  • A graph of exponential function [latex]f\left(x\right)=a^x[/latex] or [latex]y=a^x[/latex], where [latex]a>0,\;a\neq1[/latex], has no x-intercept.

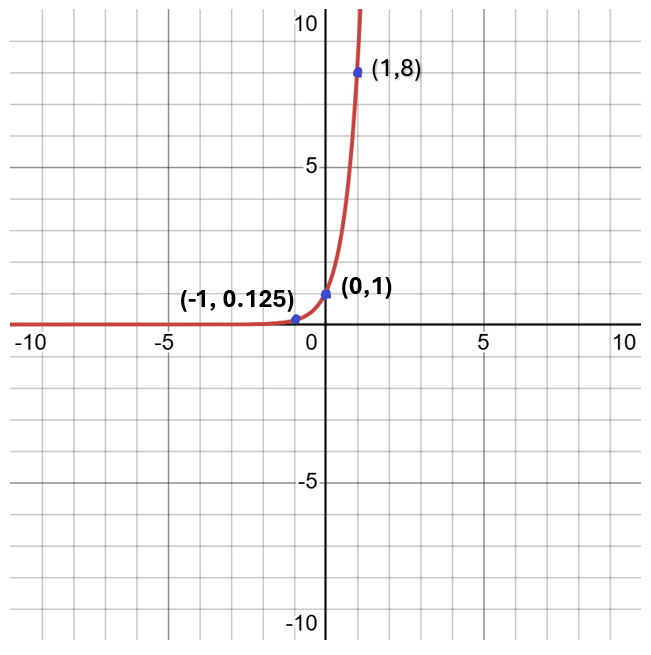
Example 3.3-2-1: Graph the function.

[latex]f\left(x\right)=8^x[/latex]

Inverselina Character Key

Example 3.3-2-1: Graph the function.

[latex]f\left(x\right)=8^x[/latex]

Based on the property, we know that x can be any value; thus, we can use a table to graph the function.

[latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}[/latex] [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol f}\mathbf{\color[rgb]{1.0, 1.0, 1.0}\left(x\right)}[/latex] [latex]\mathbf{\color[rgb]{1.0, 1.0, 1.0}\left({x,\;y}\right)}[/latex]
-1 [latex]8^{-1}=\frac18=0.125[/latex] [latex]\left(-1,\;0.125\right)[/latex]
0 [latex]8^0=1[/latex] [latex]\left(0,\;1\right)[/latex]
1 [latex]8^1=8[/latex] [latex]\left(1,\;8\right)[/latex]

A graph of an exponential function on a Cartesian coordinate system. The x-axis ranges from -10 to 10, and the y-axis ranges from -10 to 10, with grid lines at integer values. A red curve represents an increasing exponential function. It passes through three blue points, which are labeled with their coordinates: (-1, 0.125), (0, 1), and (1, 8). The curve approaches the negative x-axis asymptotically.

Master L3 Character

Tips for graphing problem works for ALL:

  1. Identify the Domain – Determine which x-values are valid for the function.
  2. Choose x-Values – Select a few values within the domain.
  3. Calculate y-Values – Plug x-values into the function to find corresponding y-values.
  4. Plot Points – Write each (x, y) as coordinates and plot them.
  5. Draw and Extend – Connect the points smoothly and extend the graph based on function properties.

A graph of a decreasing exponential function on a Cartesian coordinate system. The x and y axes intersect at the origin. A blue curve starts high in the second quadrant, passes through the point (0, 1), which is marked with a black dot and labeled, and then decreases asymptotically towards the positive x-axis in the first quadrant. The label '0 < a < 1' in blue indicates that the base 'a' of the exponential function is between 0 and 1, which accounts for the decreasing nature of the graph. Your Turn

Practice 3.3-2-1

Evaluate composite functions

Using the One-to-One Property to Solve Exponential Equations

[latex]If\;a^u=a^v,\;then\;u=v.[/latex]

  1. Rewrite the equation in the form [latex]a^u=a^v[/latex].
  2. Set [latex]u=v[/latex].
  3. Solve for the variable.
Inverselina Character

Tips:

To solve exponential equations effectively, ensure that both sides have the same base and that the coefficient of the exponential term is 1. If the bases differ, attempt to express both sides using a common base, often starting with prime numbers such as 2, 3, 5, or 7.

Useful Rules:

[latex]b=b^1[/latex] ([latex]b[/latex] is any number) when power is [latex]1[/latex], we do not write it out.
[latex]b^0=1[/latex] any number with power [latex]0[/latex] is [latex]1[/latex].
[latex]b^m\cdot b^n=b^{m+n}[/latex] multiply powers of the same base, add exponents.
[latex]\frac{b^m}{b^n}=b^{m-n}[/latex] divide powers of the same base, subtract (numerator exponent minus denominator exponent).
[latex]\left(b^m\right)^n=b^{m\cdot n}[/latex] multiple powers, multiple powers.
[latex]b^{-n}=\frac1{b^n}\;and\;\frac1{b^{-n}}=b^n[/latex] negative powers, reciprocal base, change power to positive.
[latex]\left(a\cdot b\right)^n=a^n\cdot b^n[/latex] raise a product to a power, raise power for each base.
[latex]\left(\frac ab\right)^n=\frac{a^n}{b^n}[/latex] raise fraction to a power, raise power for numerator and denominator.
[latex]\left(\frac ab\right)^{-n}=\left(\frac ba\right)^n[/latex] fraction raised to a negative power, reciprocal fraction change power to positive.

Example 3.3-3-1: Solve Elementary Exponential Equations.

[latex]3^{x+1}=81[/latex]

Inverselina Character Key

Example 3.3-3-1: Solve Elementary Exponential Equations.

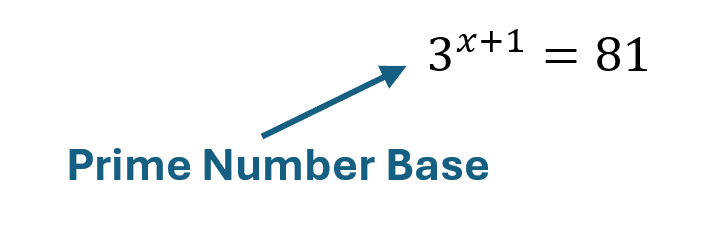
The exponential equation 3 to the power x+1 = 81 is shown. A teal arrow points from the text 'Prime Number Base' to the base of the exponential term, which is '3'.

Step 1: To have [latex]a^u=a^v[/latex] we need to rewriting [latex]81[/latex] with Base [latex]3[/latex], We choose base [latex]3[/latex] because the expression on the right side involves base [latex]3[/latex]. Additionally, [latex]3[/latex] is a prime number, meaning it cannot be reduced to any other integer base.

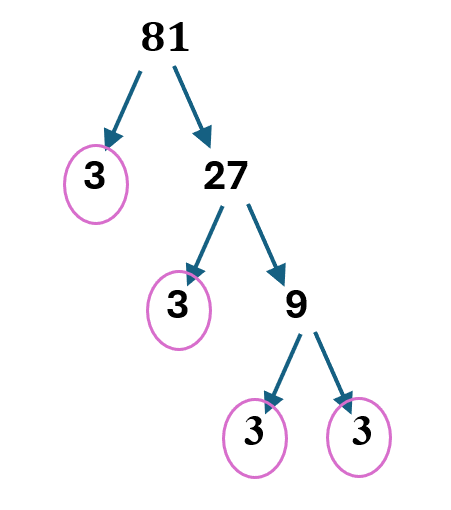
A factor tree illustrating the prime factorization of the number 81. Starting at the top, the number 81 has two downward arrows leading to its factors: 3 and 27. The number 3 is enclosed in a pink circle, indicating it is a prime factor. The number 27 has two downward arrows leading to its factors: 3 and 9. The number 3 is again enclosed in a pink circle as a prime factor. The number 9 has two downward arrows leading to its factors: 3 and 3. Both of these 3s are enclosed in pink circles, indicating they are prime factors. Therefore, the prime factorization of 81 is 3 × 3 × 3 × 3, or 3 to the power 4.

[latex]81={\color[rgb]{0.5, 0.0, 0.5}\mathbf3}^{\color[rgb]{0.5, 0.0, 0.5}\mathbf4}[/latex]

Thus:

[latex]3^{x+1}=81[/latex]

[latex]3^{x+1}={\color[rgb]{0.5, 0.0, 0.5}\mathbf3}^{\color[rgb]{0.5, 0.0, 0.5}\mathbf4}[/latex]

Step 2: Since left and right bases are the same, we just need to compare the power.

[latex]x+1=4[/latex]

Step 3: Solve for the variable.

[latex]x=4-1[/latex]

[latex]x=3[/latex]

Example 3.3-3-2: Solve Elementary Exponential Equations.

[latex]7^{x+3}=\frac17[/latex]

Inverselina Character Key

Example 3.3-3-2: Solve Elementary Exponential Equations.

The exponential equation 7^(x+3) = 1/7 is shown. A teal arrow points from the text 'Prime Number Base' to the base of the exponential term, which is '7'.

Step 1: To have [latex]a^u=a^v[/latex] we need to flip [latex]\frac17[/latex]

Based on the rule

[latex]\left(\frac ab\right)^{-n}=\left(\frac ba\right)^n[/latex]

[latex]\frac17=\left(\frac17\right)^1=\left(\frac17\right)^{-1}=7^{-1}[/latex]

Thus:

[latex]\frac17=7^{-1}[/latex]

[latex]7^{x+3}={\color[rgb]{0.5, 0.0, 0.5}\frac{\mathbf1}{\mathbf7}}[/latex]

[latex]7^{x+3}={\color[rgb]{0.5, 0.0, 0.5}\mathbf7}^{\color[rgb]{0.5, 0.0, 0.5}{\boldsymbol-\mathbf1}}[/latex]

Step 2: Since left and right bases are the same, we just need to compare the power.

[latex]x+3=-1[/latex]

Step 3: Solve for the variable.

[latex]x=-1-3[/latex]

[latex]x=-4[/latex]

Example 3.3-3-3: Solve Elementary Exponential Equations.

[latex]8^{x+2}=4^{x-3}[/latex]

Inverselina Character Key

Example 3.3-3-3: Solve Elementary Exponential Equations.

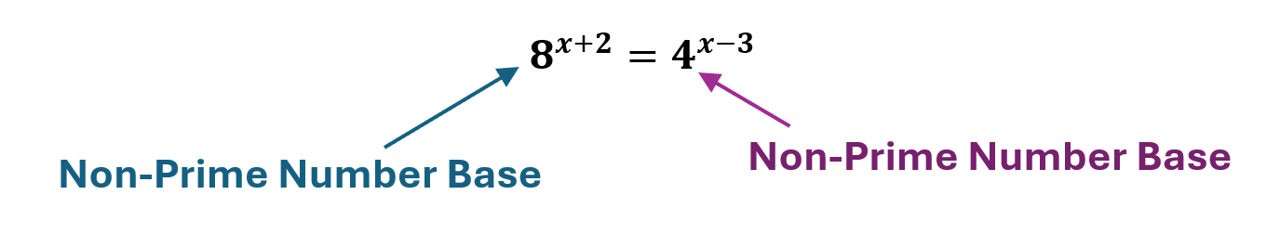
The exponential equation 8 to the power (x+2) = 4 to the power (x-3) is shown. A teal arrow points to the base of the left exponential term, '8', with the label 'Non-Prime Number Base' below it. A magenta arrow points to the base of the right exponential term, '4', also with the label 'Non-Prime Number Base' below it.

Step 1: To have [latex]a^u=a^v[/latex] we can first reduce both bases to prime numbers.

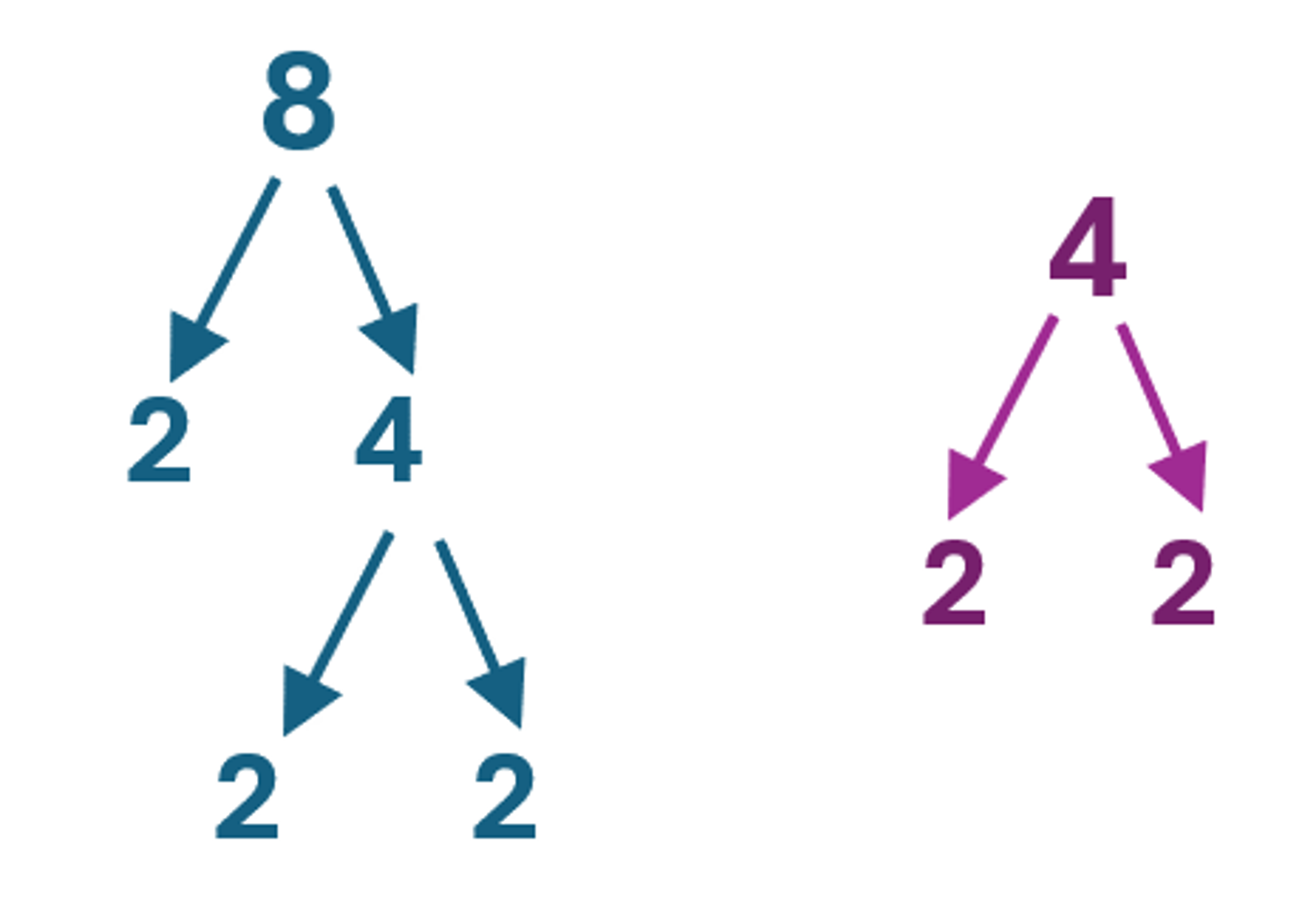
Two factor trees are shown side-by-side. The factor tree on the left, in teal, starts with the number 8. Two arrows branch down to its factors, 2 and 4. The 2 is at the end of its branch. From the 4, two more arrows branch down to its factors, 2 and 2, which are at the end of their branches. This shows the prime factorization of 8 as 2 × 2 × 2. The factor tree on the right, in magenta, starts with the number 4. Two arrows branch down to its factors, 2 and 2, which are at the end of their branches. This shows the prime factorization of 4 as 2 × 2.

Thus: [latex]8=2^3,\;4=2^2[/latex]

[latex]\left({\color[rgb]{0.0, 0.44, 0.73}\mathbf2}^{\color[rgb]{0.0, 0.44, 0.73}\mathbf3}\right)^{x+2}=\left({\color[rgb]{0.5, 0.0, 0.5}\mathbf2}^{\color[rgb]{0.5, 0.0, 0.5}\mathbf2}\right)^{x-3}[/latex]

Simplify the equation by using rule

[latex]\left(b^m\right)^n=b^{m\cdot n}[/latex]

[latex]{\color[rgb]{0.0, 0.44, 0.73}\mathbf2}^{\left({\color[rgb]{0.0, 0.44, 0.73}\mathbf3}\right)\left(x+2\right)}={\color[rgb]{0.5, 0.0, 0.5}\mathbf2}^{\left({\color[rgb]{0.5, 0.0, 0.5}\mathbf2}\right)\left(x-3\right)}[/latex]

[latex]{\color[rgb]{0.0, 0.44, 0.73}\mathbf2}^{{\color[rgb]{0.0, 0.44, 0.73}\mathbf3}x+6}={\color[rgb]{0.5, 0.0, 0.5}\mathbf2}^{{\color[rgb]{0.5, 0.0, 0.5}\mathbf2}x-6}[/latex]

Step 2: Since left and right bases are the same, we just need to compare the power.

[latex]3x+6=2x-6[/latex]

Step 3: Solve for the variable.

[latex]3x-2x+6=-6[/latex]

[latex]x+6=-6[/latex]

[latex]x=-6-6[/latex]

[latex]x=-12[/latex]

A graph of a decreasing exponential function on a Cartesian coordinate system. The x and y axes intersect at the origin. A blue curve starts high in the second quadrant, passes through the point (0, 1), which is marked with a black dot and labeled, and then decreases asymptotically towards the positive x-axis in the first quadrant. The label '0 < a < 1' in blue indicates that the base 'a' of the exponential function is between 0 and 1, which accounts for the decreasing nature of the graph. Your Turn

Practice 3.3-3-1

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Math Mastery Manual Copyright © by Linglin (Niki) Liu is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book