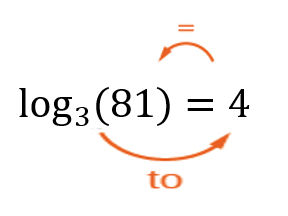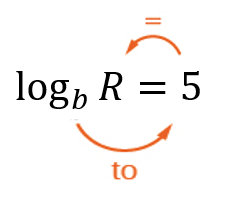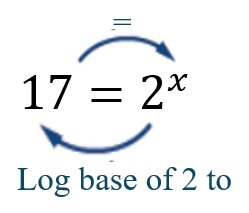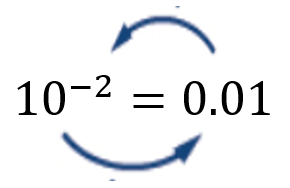"

3.4: Logarithmic Functions

Learning Objectives

  1. Determine the domain of a logarithmic function.
  2. Translate between logarithmic and exponential notation.
  3. Evaluate logarithmic expressions.
  4. Solve and graph logarithmic functions.

Logarithmic Functions

A Logarithmic function is considered the inverse function of an exponential function. That is,

If [latex]f\left(x\right)=b^x\left(x\in R\right)[/latex], then [latex]f^{-1}\left(x\right)=\log_bx\left(x>0\right),[/latex] where [latex]b>0,\;b\neq1[/latex].

If [latex]b>0,\;b\neq1[/latex], and [latex]x>0[/latex], then [latex]y=\log_b\left(x\right)[/latex] if an only if [latex]b^y=x[/latex].

We read it as “[latex]y[/latex] is the log base [latex]b[/latex] of [latex]x[/latex] ”, or “[latex]y[/latex] is the power we raise [latex]b[/latex] to get [latex]x[/latex]”

Since the logarithm is the inverse function of the exponential, thus the domain of the logarithm is the range of the exponential.

Determine the domain of a logarithmic function

Steps:

  1. Identify the variable:
    • In the expression [latex]\log_bA[/latex] the variable is [latex]A[/latex].
  2. Set the argument of the log greater than 0:
    • Since the argument of a logarithm must be positive, set: [latex]A>0[/latex]
  3. Solve for [latex]x[/latex]:
    • Use algebra or logarithmic rules (if it’s an equation) to find the value of [latex]x[/latex] in the [latex]A[/latex] that satisfies the expression or equation.

Example 3.4-1-1: Find the domain of giving the logarithmic function.

[latex]f\left(x\right)=\log_5\left(x+2\right)[/latex]

Inverselina Character Key

Example 3.4-1-1: Find the domain of giving the logarithmic function.

[latex]f\left(x\right)=\log_5\left(x+2\right)[/latex]

  1. Identify the variable:

In the expression [latex]\log_bA[/latex] the variable is [latex]A[/latex].

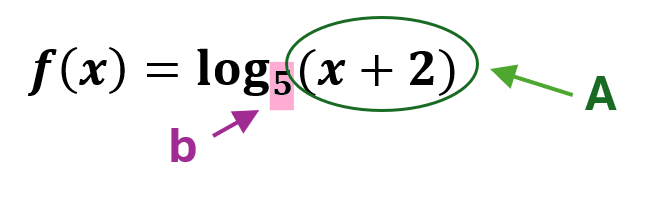
The logarithmic function f(x) = log base 5 of (x + 2) is shown. A green arrow labeled 'A' points to the argument of the logarithm, which is (x + 2) and is enclosed in a green oval. A magenta arrow labeled 'b' points to the base of the logarithm, which is 5 and is highlighted with a pink rectangle.

  1. Set the argument of the log greater than 0:

Since the argument of a logarithm must be positive, set: [latex]A>0[/latex]

[latex]x+2>0[/latex]

  1. Solve for [latex]x[/latex]:

Use algebra or logarithmic rules (if it’s an equation) to find the value of [latex]x[/latex] in the [latex]A[/latex] that satisfies the expression or equation.

[latex]x>-2[/latex]

Domain: [latex]\left(-2,\;\infty\right)[/latex]

The logarithmic function f(x) = log base 5 of (x + 2) is shown. A green arrow labeled 'A' points to the argument of the logarithm, which is (x + 2) and is enclosed in a green oval. A magenta arrow labeled 'b' points to the base of the logarithm, which is 5 and is highlighted with a pink rectangle. Your Turn

Practice 3.4-1-1

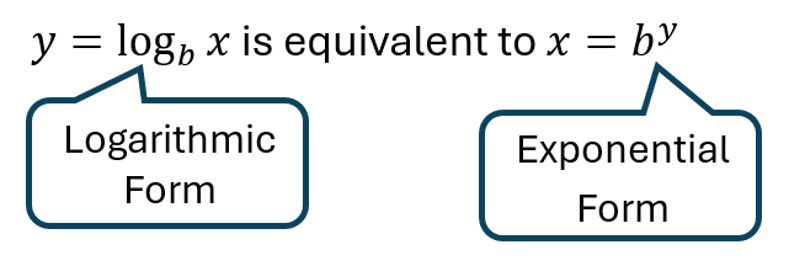
Translate between logarithmic and exponential notation

Logarithmic Function of Base [latex]b[/latex]

For [latex]x>0[/latex] and [latex]b>0,\;b\neq1,[/latex]

The equivalence between logarithmic and exponential forms is illustrated. The equation 'y = log base b of x' is shown with a speech bubble pointing to it labeled 'Logarithmic Form'. The equivalent exponential equation 'x = b to the power of y' is shown with a speech bubble pointing to it labeled 'Exponential Form'."

Arrow method:

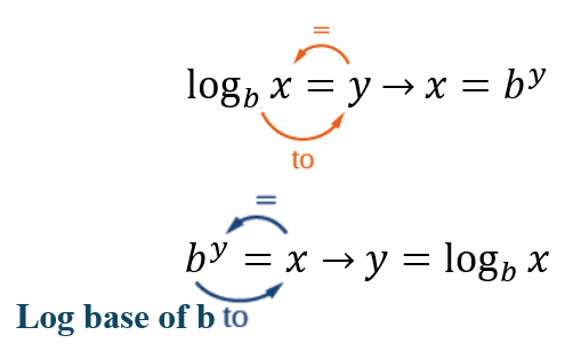
The image illustrates the conversion between logarithmic and exponential forms using circular arrows. The top part shows the logarithmic form: log base b of x equals y. An orange circular arrow indicates the transformation 'to' the exponential form: x equals b to the power of y. The arrow starts at the base 'b', goes up to 'y' as the exponent, and then points to 'x' as the result. The bottom part shows the exponential form: b to the power of y equals x. A blue circular arrow indicates the transformation 'Log base of b to' the logarithmic form: y equals log base b of x. The arrow starts at the base 'b', goes across the equals sign to 'x' as the argument of the logarithm, and then points to 'y' as the result.

Note:

Common Logarithm [latex]\log_{10}\left(x\right)=\log\left(x\right)[/latex]

Natural Logarithm [latex]\log_e\left(x\right)=\ln\left(x\right)[/latex]

Example 3.4-2-1: Converting the following logarithmic equations to exponential equations.

  1. [latex]\log_3\left(81\right)=4[/latex]
  2. [latex]\log_bR=5[/latex]
  3. [latex]y=\log\;Q[/latex]
  4. [latex]\ln x=5[/latex]

Inverselina Character Key

Example 3.4-2-1: Converting the following logarithmic equations to exponential equations.

  1. The logarithmic equation 'log base 3 of (81) equals 4' is shown. An orange circular arrow starts at the base '3', goes up to the result '4' as the exponent, and then points to the argument '81', illustrating the conversion 'to' the equivalent exponential form.
 [latex]3^4=81[/latex]
  1. The logarithmic equation 'log base b of R equals 5' is shown. An orange circular arrow starts at the base 'b', goes up to the result '5' as the exponent, and then points to the argument 'R', illustrating the conversion 'to' the equivalent exponential form.
 [latex]b^5=R[/latex]
  1. [latex]y=\log\;Q[/latex]

There is an invisible [latex]10[/latex] since it is a common logarithm; thus, we can rewrite it as

The logarithmic equation 'y equals log base 10 of Q' is shown. An orange circular arrow starts at the base '10', goes up to the result 'y' as the exponent, and then points to the argument 'Q', illustrating the conversion to the equivalent exponential form.

[latex]e^5=y[/latex]

Example 3.4-2-2: Converting the following exponential equations to logarithmic equations.

  1. [latex]17=2^x[/latex]
  2. [latex]10^{-2}=0.01[/latex]
  3. [latex]e^t=8[/latex]

Inverselina Character Key

Example 3.4-2-2: Converting the following logarithmic equations to exponential equations.

  1. The exponential equation '17 equals 2 to the power of x' is shown. A blue circular arrow starts at the base '2', goes across the equals sign to '17' as the argument of the logarithm, and then points to 'x' as the result, illustrating the conversion 'Log base of 2 to' the equivalent logarithmic form.

[latex]x=\log_2\;17[/latex]

  1. The exponential equation '10 to the power of minus 2 equals 0.01' is shown. A blue circular arrow starts at the base '10', goes across the equals sign to '0.01' as the argument of the logarithm, and then points to '-2' as the result, illustrating the conversion to the equivalent logarithmic form.

[latex]-2=\log_{10}\left(0.01\right)\rightarrow-2=\log\left(0.01\right)\;Common\;\log[/latex]

  1. The exponential equation 'e to the power of t equals 8' is shown. A blue circular arrow starts at the base 'e', goes across the equals sign to '8' as the argument of the logarithm, and then points to 't' as the result, illustrating the conversion to the equivalent logarithmic form.

[latex]t=\log_e\left(8\right)\rightarrow t=\ln\left(8\right)\;Natural\;\log[/latex]

The logarithmic function f(x) = log base 5 of (x + 2) is shown. A green arrow labeled 'A' points to the argument of the logarithm, which is (x + 2) and is enclosed in a green oval. A magenta arrow labeled 'b' points to the base of the logarithm, which is 5 and is highlighted with a pink rectangle. Your Turn

Practice 3.4-2-1

Practice 3.4-2-2

Evaluate logarithmic expressions

Given a logarithm of the form [latex]y=\log_b\left(x\right)[/latex], evaluate it mentally.

  1. Rewrite the argument [latex]x[/latex] as a power of [latex]b\;:\;b^y=x[/latex].
  2. Use previous knowledge of powers of [latex]b[/latex] identify [latex]y[/latex] by asking, “To what exponent should [latex]b[/latex] be raised in order to get [latex]x[/latex]?”

Example 3.4-2-2: Solving Logarithms Mentally

Solve [latex]y=\log_4\left(64\right)[/latex] without using a calculator.

Inverselina Character Key

Example 3.4-2-2: Solve [latex]y=\log_4\left(64\right)[/latex] without using a calculator.

First we rewrite the logarithm in exponential form: [latex]4^y=64[/latex]. Next, we ask, “To what exponent must [latex]4[/latex] be raised in order to get [latex]64[/latex]?”

We know

[latex]4^3=64[/latex]

Therefore,

[latex]\log_4\left(64\right)=3[/latex]

The logarithmic function f(x) = log base 5 of (x + 2) is shown. A green arrow labeled 'A' points to the argument of the logarithm, which is (x + 2) and is enclosed in a green oval. A magenta arrow labeled 'b' points to the base of the logarithm, which is 5 and is highlighted with a pink rectangle. Your Turn

Practice 3.4-3-1

Solve Simple Logarithms

For any logarithmic equation [latex]y=\log_bx\;or\;\log_bx=y[/latex], to find [latex]x[/latex],

  1. Translate to an exponential equation.
  2. Solve for [latex]x[/latex].
  3. Use the domain to check the answer, select the one that fits the domain [latex]\left(x>0\right)[/latex].

Example 3.4-4-1: Solve the logarithmic equation.

[latex]\log_3\left(8-x\right)=4[/latex]

Inverselina Character Key

Example 3.4-4-1: Solve the logarithmic equation.

[latex]\log_3\left(8-x\right)=4[/latex]

  1. Translate to an exponential equation.

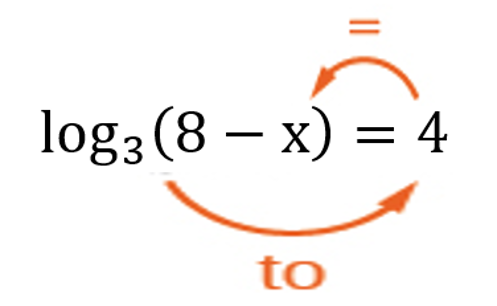
The logarithmic equation 'log base 3 of (8 minus x) equals 4' is shown. An orange circular arrow starts at the base '3', goes up to the result '4' as the exponent, and then points to the argument '(8 minus x)', illustrating the conversion 'to' the equivalent exponential form: 3 to the power of 4 equals (8 minus x).

[latex]3^4=8-x[/latex]

  1. Solve for [latex]x[/latex].

[latex]3^4=8-x[/latex]

[latex]81=8-x[/latex]

[latex]81-8=-x[/latex]

[latex]73=-x[/latex]

[latex]-73=x[/latex]

[latex]x=-73[/latex]

  1. Use the domain to check the answer, select the one that fits the domain [latex]\left(x>0\right)[/latex].

Based on the domain rule, if [latex]\log_bA,\;A>0[/latex]

Thus, we need to ensure [latex]8-x>0[/latex]

Use [latex]x= - 73[/latex] substitute [latex]x[/latex] value,

[latex]8-\left(-7\right)=81[/latex], it is positive, which is greater than 0, thus the answer is

[latex]x=-73[/latex]

The logarithmic function f(x) = log base 5 of (x + 2) is shown. A green arrow labeled 'A' points to the argument of the logarithm, which is (x + 2) and is enclosed in a green oval. A magenta arrow labeled 'b' points to the base of the logarithm, which is 5 and is highlighted with a pink rectangle. Your Turn

Practice 3.4-4-1

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Math Mastery Manual Copyright © by Linglin (Niki) Liu is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book