3.6: Logarithmic and Exponential Equations
Learning Objectives
- Solve complex exponential equations.
- Solve complex logarithmic equations.
Recall
Section 3.3: Solve exponential equations
[latex]If\;a^u=a^v,\;then\;u=v.[/latex]
- Rewrite the equation in the form [latex]a^u=a^v[/latex].
- Set [latex]u=v[/latex].
- Solve for the variable.
Section 3.4: Translate between exponents and logarithms
Arrow method:
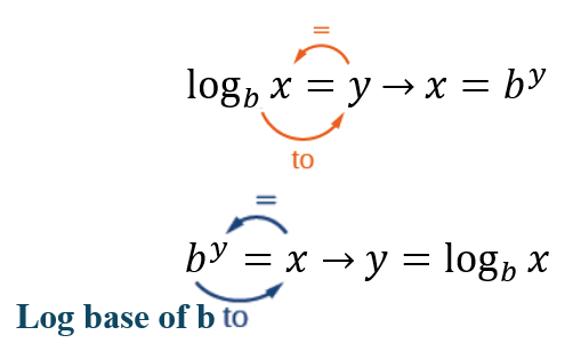
Note:
Common Logarithm [latex]\log_{10}\left(x\right)=\log\left(x\right)[/latex]
Natural Logarithm [latex]\log_e\left(x\right)=\ln\left(x\right)[/latex]
Section 3.5: Properties of logarithms
Change-of-Base Formula:
[latex]If\;a,\;b,\;x\in\mathbb{R}\;and\;a,\;b,\;x>0\;and\;a,\;b\;\neq1,[/latex]
[latex]\log_b\left(x\right)=\frac{\log_a\left(x\right)}{\log_a\left(b\right)}=\frac{\log\left(x\right)}{\log\left(b\right)}=\frac{\ln\left(x\right)}{\ln\left(b\right)}[/latex]
If the logarithmic base is neither 10 nor e, we need to convert it to a common base, such as 10 or e, to evaluate the logarithm.
[latex]If\;a,\;b,\;x\in\mathbb{R}\;and\;a,\;b,\;x>0\;and\;a,\;b\;\neq1,[/latex]
[latex]\log_a\left(M\right)=\frac{\log_b\left(M\right)}{\log_b\left(a\right)}=\frac{\log\left(M\right)}{\log\left(a\right)}=\frac{\ln\left(M\right)}{\ln\left(a\right)}[/latex]
- [latex]\log_aa^r=r[/latex]
- [latex]\log_a\left(MN\right)=\log_a\left(M\right)+\log_a\left(N\right)[/latex]
- [latex]\log_a\left(\frac MN\right)=\log_aM-\log_aN[/latex]
- [latex]\log_aM^r=r\log_aM[/latex]
- [latex]\log_aM=\frac{\log\;M}{\log\;a}=\frac{\ln\;M}{\ln\;a}[/latex]
Note:
|
|
Solve complex exponential equations
For more complex exponential equations, we can no longer apply the strategies used in Section 3.3, as it’s often difficult to rewrite both sides with the same base. Instead, we use the inverse function of an exponential — the logarithm — to rewrite the equation in a form that allows us to bring down the exponent and solve for the variable.
Steps:
- Ensure the equation has exponential expressions on both sides with a coefficient of 1, or one side is an exponential expression with a coefficient of 1 and the other side is a constant.
- Apply a logarithm (either ln or log) to both sides of the equation.
- Use logarithmic properties to bring the exponent down in front.
Example 3.6-1-1: Solve the exponential equation
[latex]3^{x+6}=15[/latex]
 Key
Key
Example 3.6-1-1: Solve the exponential equation
[latex]3^{x+6}=15[/latex]
- Ensure the equation has exponential expressions on both sides with a coefficient of 1, or one side is an exponential expression with a coefficient of 1 and the other side is a constant.
Yes, so go to step 2.
- Apply a logarithm (either ln or log) to both sides of the equation.

We use either ln or log, in here I will use [latex]ln[/latex].
Why? 
Because it has just two letters instead of three.
[latex]\ln\left(3^{x+6}\right)=\ln\left(15\right)[/latex]
- Use logarithmic properties to bring the exponent down in front.
Use: [latex]\log_a\;M^r=r\log_a\;M[/latex]
[latex]\left(x+6\right)\ln\left(3\right)=\ln\left(15\right)[/latex]
- Solve for [latex]x[/latex].

To solve for [latex]x[/latex], the most challenging part here is that we must get used to treating ln as an operation and handle it like a regular number.
[latex]\left(x+6\right)\ln\left(3\right)=\ln\left(15\right)[/latex]
[latex]x\cdot\ln\left(3\right)+6\ln\left(3\right)=\ln\left(15\right)[/latex]
[latex]x\cdot\ln\left(3\right)=\ln\left(15\right)-6\ln\left(3\right)[/latex]
[latex]\frac{x\cdot\ln\left(3\right)}{{\color[rgb]{0.5, 0.0, 0.5}\boldsymbol l}{\color[rgb]{0.5, 0.0, 0.5}\boldsymbol n}\mathbf{\color[rgb]{0.5, 0.0, 0.5}\left(3\right)}}=\frac{\ln\left(15\right)-6\ln\left(3\right)}{{\color[rgb]{0.5, 0.0, 0.5}\boldsymbol l}{\color[rgb]{0.5, 0.0, 0.5}\boldsymbol n}\mathbf{\color[rgb]{0.5, 0.0, 0.5}\left(3\right)}}[/latex]
[latex]x=\frac{\ln\left(15\right)-6\ln\left(3\right)}{{\color[rgb]{0.5, 0.0, 0.5}\boldsymbol l}{\color[rgb]{0.5, 0.0, 0.5}\boldsymbol n}\mathbf{\color[rgb]{0.5, 0.0, 0.5}\left(3\right)}}[/latex]
Example 3.6-1-2: Solve the exponential equation
[latex]14=2e^x[/latex]
 Key
Key
Example 3.6-1-2: Solve the exponential equation
[latex]14=2e^x[/latex]
- Ensure the equation has exponential expressions on both sides with a coefficient of 1, or one side is an exponential expression with a coefficient of 1 and the other side is a constant.
We need to divide both sides by [latex]2[/latex], since the base of the exponent on [latex]x[/latex] is [latex]e[/latex], not [latex]2e[/latex].
- Apply a logarithm (either ln or log) to both sides of the equation.
[latex]14=2e^x[/latex]
[latex]7=e^x[/latex]

We use either ln or log, in here I will use [latex]ln[/latex].
Why?
This time it was not just because ln is two letters, but also the base is e, so if we use ln, it can be simplified a little more.
[latex]\ln\left(7\right)=\ln\left(e^x\right)[/latex]
- Use logarithmic properties to bring the exponent down in front.
Use: [latex]\log_a\;M^r=r\log_a\;M[/latex]
[latex]\ln\left(7\right)=x\ln\left(e\right)[/latex]
[latex]\ln\left(7\right)=x[/latex]
[latex]\log_a\;a=1,\;and\;\log_e\left(e\right)=\ln\left(e\right),\;thus\;we\;have\;\log_e\left(e\right)=\ln\left(e\right)=1[/latex]
- Solve for [latex]x[/latex].
Step 3 already gave the answer, so additional steps are needed.
[latex]x=\ln\left(7\right)[/latex]
 Your Turn
Your Turn
Practice 3.6-1-1
Solve complex logarithmic equations
Type 1: Both sides with logs
If an equation has logarithms on both sides, follow these steps:
Step 1: Simplify Each Side: Make sure each side contains only one logarithmic expression each side.
- If a logarithm has a coefficient, use the power rule:
[latex]r\log_aM=\log_aM^r[/latex]
- If there are multiple logarithms on one side, condense them:
Use the quotient rule: [latex]\log_aM-\log_aM=\log_a\left(\frac MN\right)[/latex]
Use the product rule: [latex]\log_aM+\log_aM=\log_a\left(MN\right)[/latex]
Step 2: Drop the Logs (If Bases Match)
- After condensing, if both sides have the same log base, you can drop the logarithms and set the remaining expressions equal:
[latex]\log_a\left(A\right)=\log_a\left(B\right)[/latex]
[latex]\cancel{\log_a}\left(A\right)=\cancel{\log_a}\left(B\right)[/latex]
[latex]A=B[/latex]
Step 3: Solve for the Variable
- Solve the resulting algebraic equation for the unknown variable (e.g., [latex]x[/latex]).
Step 4: Check for Extraneous Solutions
- Always check your answers in the original equation.
- Make sure the values keep the arguments of all logarithms positive (since log functions are undefined for zero or negative inputs).
Example 3.6-2-1: Solve the logarithm equation
[latex]\log_4\left(2x-5\right)+\log_4\left(x\right)=\log_4\left(3\right)[/latex]
 Key
Key
Example 3.6-2-1: Solve the logarithm equation
[latex]\log_4\left(2x-5\right)+\log_4\left(x\right)=\log_4\left(3\right)[/latex]
Step 1: Simplify Each Side: Make sure each side contains only one logarithmic expression each side.
- there are multiple logarithms on one side, condense them:
[latex]\begin{array}{c}\log_4\left(2x-5\right){\color[rgb]{0.5, 0.0, 0.5}\boxed{\color[rgb]{0.1, 0.1, 0.1}\mathbf+}}\log_4\left(x\right)=\log_4\left(3\right)\end{array}[/latex]
We see “[latex]+[/latex]”, thus use the product rule: [latex]\log_aM+\log_aN=\log_a\left(MN\right)[/latex]
[latex]\log_4\left(\left(2x-5\right)\left(x\right)\right)=\log_4\left(3\right)[/latex]
Step 2: Drop the Logs (If Bases Match)
- After condensing, if both sides have the same log base, you can drop the logarithms and set the remaining expressions equal:
[latex]\log_4\left(\left(2x-5\right)\left(x\right)\right)=\log_4\left(3\right)[/latex]
[latex]\cancel{\log_4}\left(\left(2x-5\right)\left(x\right)\right)=\cancel{\log_4}\left(3\right)[/latex]
[latex]\left(2x-5\right)\left(x\right)=3[/latex]
Step 3: Solve for the Variable
- Solve the resulting algebraic equation for the unknown variable (e.g., x).
[latex]\left(2x-5\right)\left(x\right)=3[/latex]
[latex]2x^2-5x=3 Since\;variable's\;highest\;power\;is\;2;it\;is\;a\;quadratic\;function.[/latex]
[latex]2x^2-5x-3=0[/latex]
[latex]\left(x+\frac12\right)\left(x+\frac{-6}2\right)=0 AC\;method[/latex]
[latex]\left(x+\frac12\right)\left(x-3\right)=0[/latex]
[latex]x=\frac12,\;x=3[/latex]
Step 4: Check Solutions
[latex]\log_4\left(2x-5\right)+\log_4\left(x\right)=\log_4\left(3\right)[/latex]
Based on the domain, we must ensure [latex]2x-5>0[/latex], and [latex]x>0[/latex], thus we can use a table to check.
| Potential Answer | [latex]{\color[rgb]{1.0, 1.0, 1.0}\mathbf2}{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}{\color[rgb]{1.0, 1.0, 1.0}\mathbf-}{\color[rgb]{1.0, 1.0, 1.0}\mathbf5}[/latex] | [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}[/latex] |
|---|---|---|
| [latex]-\frac12[/latex] | [latex]2\left(-\frac12\right)-5=1-5={\color[rgb]{0.0, 0.44, 0.73}\mathbf-}{\color[rgb]{0.0, 0.44, 0.73}\mathbf4}[/latex]
Negative value conflicts with the domain, so we exclude [latex]-\frac12[/latex] as a solution. |
|
| [latex]3[/latex] | [latex]2\left(3\right)-5=1[/latex]
Positive value. [latex]{\color[rgb]{0.0, 0.44, 0.73}\mathbf\checkmark}[/latex] |
[latex]3[/latex]
Positive value. [latex]{\color[rgb]{0.0, 0.44, 0.73}\mathbf\checkmark}[/latex] |
Thus [latex]x=3[/latex] is the answer.
 Your Turn
Your Turn
Practice 3.6-2-1
Type 2: One side with log, another is constant
If an equation has logarithms on one side, another side is constant we follow these steps:
Step 1: Simplify Logs: Make sure log side ccontains only one logarithmic expression.
- If a logarithm has a coefficient, use the power rule:
[latex]r\log_aM=\log_aM^r[/latex]
- If there are multiple logarithms on one side, condense them:
Use the quotient rule: [latex]\log_aM-\log_aM=\log_a\left(\frac MN\right)[/latex]
Use the product rule: [latex]\log_aM+\log_aM=\log_a\left(MN\right)[/latex]
Step 2: Arrow method.
- After condensing use arrow method convert it to exponential equation.
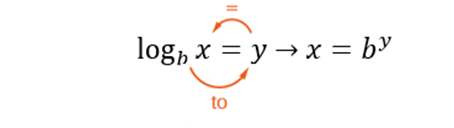
Step 3: Solve for the Variable
- Solve the resulting algebraic equation for the unknown variable (e.g., x).
Step 4: Check for Extraneous Solutions
- Always check your answers in the original equation.
- Make sure the values keep the arguments of all logarithms positive (since log functions are undefined for zero or negative inputs).
Example 3.6-2-2: Solve the logarithm equation
[latex]2\log_4\left(x+2\right)=2[/latex]
 Key
Key
Example 3.6-2-2: Solve the logarithm equation
[latex]2\log_4\left(x+2\right)=2[/latex]
Step 1: Simplify Logs: Make sure log side contains only one logarithmic expression.
- If a logarithm has a coefficient, use the power rule:
[latex]r\log_aM=\log_aM^r[/latex]
[latex]2\log_4\left(x+2\right)=2[/latex]
[latex]\log_4\left(x+2\right)^2=2[/latex]
Step 2: Arrow method.
- After condensing use arrow method convert it to exponential equation.
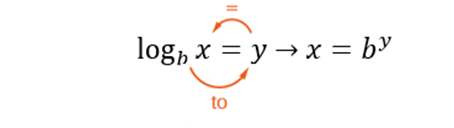
[latex]\log_4\left(x+2\right)^2=2[/latex]
[latex]4^2=\left(x+2\right)^2[/latex]
Step 3: Solve for the Variable
- Solve the resulting algebraic equation for the unknown variable (e.g., x).
[latex]16=x^2+4x+4[/latex]
[latex]0=x^2+4x+4-16[/latex]
[latex]0=x^2+4x-12[/latex]
[latex]0=\left(x+6\right)\left(x-2\right)[/latex]
[latex]x=-6,\;x=2[/latex]
Step 4: Check for Extraneous Solutions
Based on the domain, we must ensure [latex]x+2>0[/latex], thus we can use a table to check.
[latex]2\log_4\left(x+2\right)=2[/latex]
| Potential Answer | [latex]{\color[rgb]{1.0, 1.0, 1.0}\boldsymbol x}{\color[rgb]{1.0, 1.0, 1.0}\mathbf+}{\color[rgb]{1.0, 1.0, 1.0}\mathbf2}[/latex] |
|---|---|
| [latex]-6[/latex] | [latex]-6+2={\color[rgb]{0.0, 0.44, 0.73}\mathbf-}{\color[rgb]{0.0, 0.44, 0.73}\mathbf4}[/latex]
Negative value conflicts with the domain, so we exclude [latex]-6[/latex] as a solution. |
| [latex]2[/latex] | [latex]2+2={\color[rgb]{0.0, 0.44, 0.73}\mathbf4}[/latex]
Positive value. [latex]{\color[rgb]{0.0, 0.44, 0.73}\mathbf\checkmark}[/latex] |
Thus [latex]x=2[/latex] is the answer.
 Your Turn
Your Turn
Practice 3.6-2-2
Licenses and Attribution
CC Licensed Content
- College-algebra-2e by Jay Abramson is licensed CC BY. Access for free.
References
- OpenMoji. (n.d.). Library. https://openmoji.org/library/

