4.1: Systems of Linear Equations: Substitution and Elimination
Learning Objectives
- Identify dependent systems of equations and give their solutions.
- Identify inconsistent systems of equations.
- Solve systems of equations by substitution.
- Solve systems of equations by elimination.
Types of Linear Systems
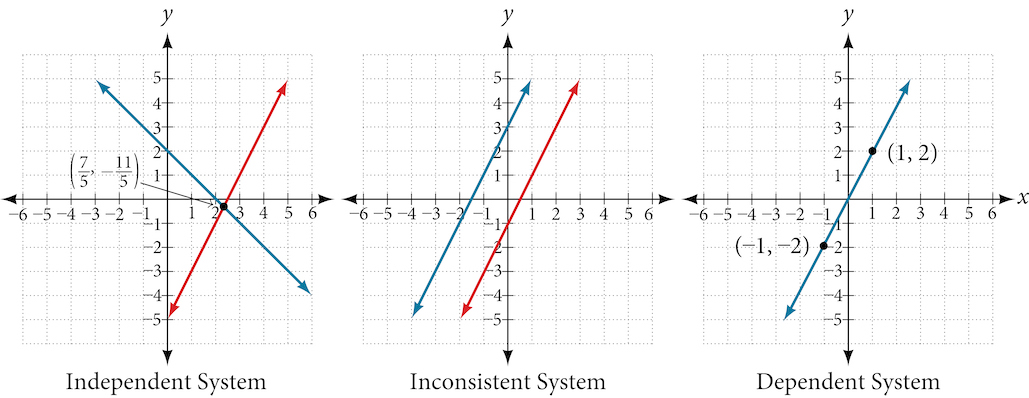
There are three types of systems of linear equations in two variables, and three types of solutions.
- An independent system has exactly one solution pair (x,y). The point where the two lines intersect is the only solution.
- An inconsistent system has no solution. Notice that the two lines are parallel and will never intersect.
- A dependent system has infinitely many solutions. The lines are coincident. They are the same line, so every coordinate pair on the line is a solution to both equations.
Solve systems of equations by substitution
Substitution Method
- Name your equation.
- Pick one equation and isolate for one of its variables. Choose the easiest variable to isolate—preferably one with a coefficient of 1 or -1.
- Substitute this expression into the other equation, replacing the variable with your solution from the previous step.
- Solve the resulting equation. This will give you one of the coordinates.
Note:
- If the equation simplifies to a true statement (e.g., 5 = 5, 0=0), the lines are the same (infinite solutions).
- If it simplifies to a false statement (e.g., 0 = -3, 0=5), the lines are parallel (no solution).
- Plug your solution into either of the original equations (preferably the simpler one) to find the other coordinate.
- Write your final answer as coordinate (a point).
Example 4.1-3-1: Solve the following systems using substitution.
[latex]\left\{\begin{array}{l}-x+y=-5\\2x-5y=1\end{array}\right.[/latex]
Key
Example 4.1-3-1: Solve the following systems using substitution.
[latex]\left\{\begin{array}{l}-x+y=-5\\2x-5y=1\end{array}\right.[/latex]
- Name your equation.
[latex]\left\{\begin{array}{lc}-x+y=-5&\boxed a\\2x-5y=1&\boxed b\end{array}\right.[/latex]
- Pick one equation and isolate for one of its variables. Choose the easiest variable to isolate—preferably one with a coefficient of 1 or -1.
Since the equation [latex]\boxed a[/latex] is simpler and the variable y has a coefficient of 1, isolating y is easier.
[latex]-x+y=-5[/latex]
[latex]\begin{array}{c}y=-5+x {\boxed a}_{new}\end{array}[/latex]
- Substitute this expression into the other equation, replacing the variable with your solution from the previous step.
Put [latex]\begin{array}{c}{\boxed a}_{new}\end{array}[/latex] in [latex]\boxed b[/latex]
[latex]2x-5{\color[rgb]{0.0, 0.44, 0.73}\boldsymbol y}=1[/latex]
[latex]2x-5{\color[rgb]{0.1, 0.1, 0.1}\left({\color[rgb]{0.0, 0.44, 0.73}\mathbf-}{\color[rgb]{0.0, 0.44, 0.73}\mathbf5}{\color[rgb]{0.0, 0.44, 0.73}\mathbf+}{\color[rgb]{0.0, 0.44, 0.73}\mathbf x}\right)}=1[/latex]
- Solve the resulting equation. This will give you one of the coordinates.
[latex]2x+25-5x=1[/latex]
[latex]25-3x=1[/latex]
[latex]-3x=-24[/latex]
[latex]x=8[/latex]
- Plug your solution into either of the original equations (preferably the simpler one) to find the other coordinate.
Since equation [latex]\boxed a[/latex] is simpler, thus use [latex]x={\color[rgb]{0.0, 0.44, 0.73}\mathbf8}[/latex] and function [latex]\boxed a[/latex] to find y.
[latex]-{\color[rgb]{0.0, 0.44, 0.73}\boldsymbol x}{\color[rgb]{0.1, 0.1, 0.1}+}{\color[rgb]{0.1, 0.1, 0.1}y}{\color[rgb]{0.1, 0.1, 0.1}=}{\color[rgb]{0.1, 0.1, 0.1}-}{\color[rgb]{0.1, 0.1, 0.1}5}[/latex]
[latex]-{\color[rgb]{0.1, 0.1, 0.1}\left({\color[rgb]{0.0, 0.44, 0.73}\mathbf8}\right)}{\color[rgb]{0.1, 0.1, 0.1}+}{\color[rgb]{0.1, 0.1, 0.1}y}{\color[rgb]{0.1, 0.1, 0.1}=}{\color[rgb]{0.1, 0.1, 0.1}-}{\color[rgb]{0.1, 0.1, 0.1}5}[/latex]
[latex]-8{\color[rgb]{0.1, 0.1, 0.1}+}{\color[rgb]{0.1, 0.1, 0.1}y}{\color[rgb]{0.1, 0.1, 0.1}=}{\color[rgb]{0.1, 0.1, 0.1}-}{\color[rgb]{0.1, 0.1, 0.1}5}[/latex]
[latex]{\color[rgb]{0.1, 0.1, 0.1}y}{\color[rgb]{0.1, 0.1, 0.1}=}{\color[rgb]{0.1, 0.1, 0.1}3}[/latex]
- Write your final answer as coordinate (a point).
Solution: [latex](8, 3)[/latex]
Your Turn
Practice 4.1-3-1
Example 4.1-3-2: Solve the following systems using substitution.
[latex]\left\{\begin{array}{l}7x+y=4\\14x+2y=1\end{array}\right.[/latex]
Key
Example 4.1-3-2: Solve the following systems using substitution.
[latex]\left\{\begin{array}{l}7x+y=4\\14x+2y=1\end{array}\right.[/latex]
- Name your equation.
[latex]\left\{\begin{array}{lc}7x+y=4&\boxed a\\14x+2y=1&\boxed b\end{array}\right.[/latex]
- Pick one equation and isolate for one of its variables. Choose the easiest variable to isolate—preferably one with a coefficient of 1 or -1.
Since the equation [latex]\boxed a[/latex] is simpler and the variable y has a coefficient of 1, isolating y is easier.
[latex]7x+y=4[/latex]
[latex]y=4-7x {\boxed a}_{new}[/latex]
- Substitute this expression into the other equation, replacing the variable with your solution from the previous step.
Put [latex]\begin{array}{c}{\boxed a}_{new}\end{array}[/latex] in [latex]\boxed b[/latex]
[latex]14x+2{\color[rgb]{0.0, 0.44, 0.73}\boldsymbol y}=1[/latex]
[latex]14x-2\left({\color[rgb]{0.0, 0.44, 0.73}\mathbf4}{\color[rgb]{0.0, 0.44, 0.73}\mathbf-}{\color[rgb]{0.0, 0.44, 0.73}\mathbf7}{\color[rgb]{0.0, 0.44, 0.73}\boldsymbol x}\right)=1[/latex]
- Solve the resulting equation. This will give you one of the coordinates.
[latex]14x-8+14x=1[/latex]
[latex]-8=1[/latex]
False statement, the lines are parallel (no solution).
Answer: no solution
Your Turn
Practice 4.1-3-2
Solve systems of equations by elimination
Elimination (Additive) Method
- If necessary, rewrite both equations in the form [latex]Ax + By = C.[/latex]
- Name your equation.
- Multiply one or both equations by constants so that the coefficients of one variable are opposites.
- Add the equations to eliminate that variable.
Note:
- If the result is a true statement (e.g., 5 = 5), the lines are the same (infinite solutions).
- If the result is a false statement (e.g., 0 = –3), the lines are parallel (no solution).
- Plug your solution into either of the original equations (preferably the simpler one) to find the other coordinate.
- Write your final answer as coordinate (a point).
Example 4.1-4-1: Solve the following systems using substitution.
[latex]\left\{\begin{array}{l}3x+5y=-11\\-2y+x=11\end{array}\right.[/latex]
Key
Example 4.1-4-1: Solve the following systems using substitution.
[latex]\left\{\begin{array}{l}3x+5y=-11\\-2y+x=11\end{array}\right.[/latex]
- If necessary, rewrite both equations in the form [latex]Ax + By = C.[/latex]
[latex]\left\{\begin{array}{l}3x+5y=-11\\x-2y=11\end{array}\right.[/latex]
- Name your equation.
[latex]\left\{\begin{array}{lc}3x+5y=-11&\boxed a\\x-2y=11&\boxed b\end{array}\right.[/latex]
- Multiply one or both equations by constants so that the coefficients of one variable are opposites.
[latex]-3\cdot\boxed b[/latex]
[latex]-3\left(x-2y\right)=-3\left(11\right)[/latex]
[latex]\begin{array}{cc}-3+6y=-33&{\boxed b}_{new}\end{array}[/latex]
- Add the equations to eliminate that variable.
[latex]\begin{array}{r}-3x+6y=-33 {\boxed b}_{new}\\+3x+5y=-11 \boxed a\\\hline0+11y=-44\\11y=-4\\y=-4\end{array}[/latex]
- Plug your solution into either of the original equations (preferably the simpler one) to find the other coordinate.
Since equation [latex]\boxed b[/latex] is simpler, thus use [latex]y={\color[rgb]{0.0, 0.44, 0.73}\mathbf-}{\color[rgb]{0.0, 0.44, 0.73}\mathbf4}[/latex] and function [latex]\boxed b[/latex] to find y.
[latex]x-2{\color[rgb]{0.0, 0.44, 0.73}\boldsymbol y}=11[/latex]
[latex]x-2\left({\color[rgb]{0.0, 0.44, 0.73}\mathbf-}{\color[rgb]{0.0, 0.44, 0.73}\mathbf4}\right)=11[/latex]
[latex]x+8=11[/latex]
[latex]x=3[/latex]
- Write your final answer as coordinate (a point).
Solution: [latex](3, -4)[/latex]
